前回は運動する観測者のための速度合成を説明しましたが、今回は「光の運動量保存則」です。 相対論は慣性系(特殊)か加速系(一般)で分けました。 本原理は観測者の運動を考慮した系間の統一的な保存則を、相対論と量子論へ提供します。

1、運動エネルギーが1/2な訳.
(A), 観測者の運動を考慮しない場合, 観測対象の波動速度を時間軸に, 前進速度を空間軸に置き, 基準系の光速度をピタゴラスの定理の和に固定します.
c² = v² + w² (1).
(B), 観測者の運動を考慮する場合, 基準系の光速度を時間軸に固定し, 後退速度を空間軸に置き, 波動速度はピタゴラスの定理の和になります.
w² = c² + v² (2).
いずれの場合も運動に対する波動速度の変化は, ( v ≪ c )場合のルートの近似である「絶対静止基準系 + ニュートン力学」の運動エネルギーとほぼ一致します.
1 ± ( v / c )² / 2 = 1 ± β² / 2 (3).
特殊相対論による補正(2次ドップラー効果)
GPS 衛星の速度(3.874 km/sec)により、GPS 衛星上での時間は地 表より遅くなります。その大きさは、( v / c )²/2 = -8.4x10⁻¹¹です。
例えば, 波動速度の変化のGPS衛星に搭載された原子時計と地表の時計の進み方の厳密解は,
地表の光速度( c ) : 299,792,458 m/s.
地心重力定数( GM ) : 3.986e + 14 m³/s².
地球半径( r ) : 6,378,000 m.
双曲線無限の波動速度, w∞ = √( c² + 2GM / r ).
GPS衛星の高度( h ) : 20,200,000 m.
GPS衛星の軌道速度( v ) : 3,874 m / s.
GPS衛星の波動速度, wg = √( w∞² - 2GM /( r + h ) - v² ).
時計の進み方の違い, wg / c = 1 + 4.45e-10.
2、光の運動量保存則.
光速度を基準系にする場合, 静止質量を等価にするのでは無く、光の運動量を等価にする必要があります. しかしながら「光速度の基準系 + ニュートン力学」は光の運動量やエネルギーの表式がないため, 光速度の基準系の等価式を定義する必要があります.
絶対静止基準系 : 質量の等価
↓
光速度の基準系 : 光の運動量の等価
アインシュタインは一般相対論を構築する前提として, 重力質量と慣性質量によるアインシュタインの等価原理を仮定しました.
アインシュタイン自身はこの二つの質量をどう考えていたのでしょう? 1948年6月19日付けでLincoln Barnettという知人に送った手紙に、「M=m/√(1-(v⁄c)^2 )を導入するのは、それに明確な定義を与えることが不可能なので、よくありません。‘静止質量’m 以外の質量は導入しない方がよい。M を導入する代りに、運動物体の運動量とエネルギーの表式を話に出す方がよいのです。」とあり、また、1989年にロシア人物理学者 Lev B. Okunは、普通に相対論的質量と呼ばれるM は使わないようにしようという提案を初めてしました。
不可能な理由は, 真空中の光速の変化を「光速度不変の原理」によって固定しているからです.
歴史的には,アインシュタインは重力の理論として一般相対論を構築するさ い,一般相対性原理と等価原理を用いた.両者とも「原理」らしい原理ではある が,等価原理を使って局所的に特殊相対論を使うわけである.ところが上述した ように,特殊相対論は光速度不変性という原理らしからぬ原理に基づいて構築さ れたわけだから,それを引きずっている一般相対論も,この経験則的原理のうえ に立脚することになってしまった.

この相対論的質量(mr)を運動している物体のエネルギー(E)に置き換えても問題の本質は同じで、アインシュタインの『質量とエネルギーの等価性の初等的証明』からも, この質量は不変ではありません.
M' - M = E/c^2 この方程式は、エネルギーと質量の等価性の法則を表示している。 エネルギー増加 E は、質量増加、E/c^2 と結合している。 エネルギーは、通常の定義に従へば、付加定数が要らないから、E = Mc^2。
慣性質量だけにエネルギーの増減と質量のスケール変化を押し付けるは無理で、エネルギーの増減と質量のスケール変化は必ずしも一致しません.
E ≠ m₀・c² / √( 1 - β² ) (4).
mr ≠ m₀ / √( 1 - β² ) (5).
重力質量はエネルギーの増加または減少であり,
E = E₀ ± p・c = m₀・c² ± p・c = mg・c² = γ・mi ・w² (6).
慣性質量は, 運動による重力質量のスケール変化であり、
mi = γ・mg = mg / √(1 ± β²) (7).
系間の真空中の光速が変化しても, この光の運動量が不変なのです.
γ = c / w = mi / mg = c / √( c² ± v² ) (8).
スケールファクター( γ )は, 波動速度( w )に対する光速度( c )の比 = 慣性質量( mi )と重力質量( mg )の比です. 静止している場合のみ(オブザーバーと同じ慣性フレーム),
γ₀ = 1, c = w₀, mg = m₀ (9),
これが光速度の基準系になります.
3、水星の近日点移動誤差の厳密解.
したがって( mg ≒ mi )の質量等価も( v ≪ c )の場合の低速近似であり, 運動する物体には( mg ≠ mi )の厳密解があります.
従って「自由落下する物体の軌跡が物体によらない」と言う原理から重力質量と慣性質量の比 mg/mi が物体によらず一定である事が導かれる。この一定値を 1 となるように単位を選べば重力質量と慣性質量が同一となる。
良い例として, 「光の運動量保存則」による水星の近日点移動誤差の補正は, 以下です.
43秒角 / 100年の誤差は, ニュートンの力のつり合い式の厳密解から出てきます.
ニュートン力学から水星の近日点運動の厳密解
また, 量子仮説は量子論的相対性原理( δλ・δmi = h / c ...波長と慣性質量の不確定性関係)にも関連しているため, 以下のような重力質量と慣性質量の違いによる問題は発生しません.
w = f・λ = h・f / ( mi・c ) (11).
実はうまくいかない理由はある程度わかっています。これは質量を持つ物体の「大きさ」が一般相対論と量子力学で反対の振舞いをすることに関係しています。一般相対論によるとブラックホールの大きさは質量に比例します。一方,量子力学によると物体は波のように振舞い,その波長はその物体の質量に反比例します。つまり,物体の大きさの目安となる長さは,重力では質量に比例し,量子論では質量に反比例する,という具合に完全に反対になっていて,これが重力と量子論を一緒に考えることが難しい原因なのです。
4、お互い様の強調はわがまま.
以上のようにスケールには大小差があり、すべての物理量は連動しています。
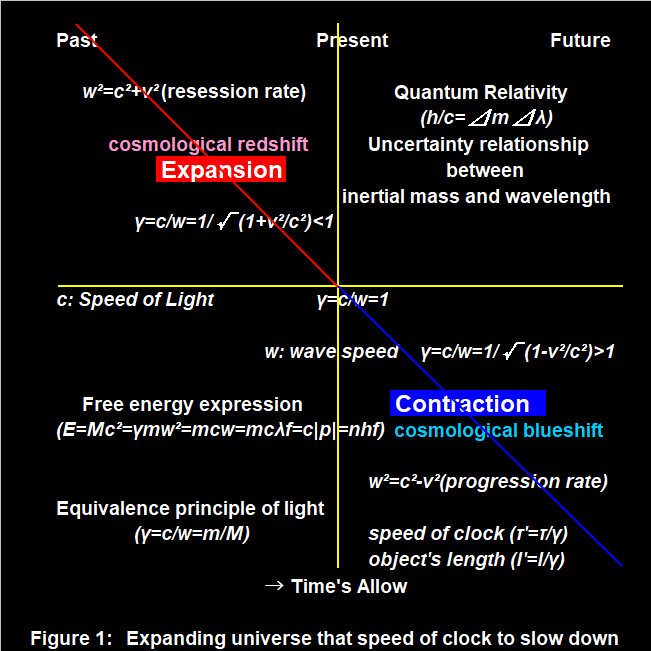
したがって「光速度不変の原理」と「質量の等価原理」のどちらかで固定するやり方はボタンのかけ間違いで, お互い様のわがままを強要する制限にしかなりません.
マーフィーの法則:「お互い様」を強調するのは、常にわがままを押し通そうとする側である。









