前回、「Bカーブの可変抵抗でCカーブを作る」を投稿しましたが、同様にAカーブを作る件も考察してみました。
参考にした記事は、前回と同じ。
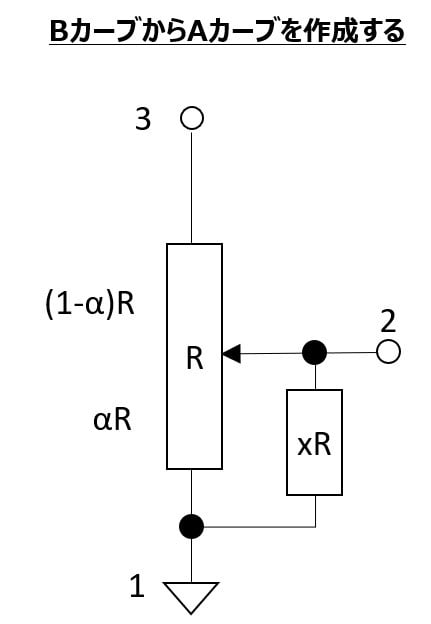
回路図はこれ。
ただ、Cカーブのようにはうまくいかず、悩んだ末、抵抗値としての絶対値ではなく、1-3端子間にたいする1-2端子間の抵抗値の比率がAカーブになる、ということで、理解しました。
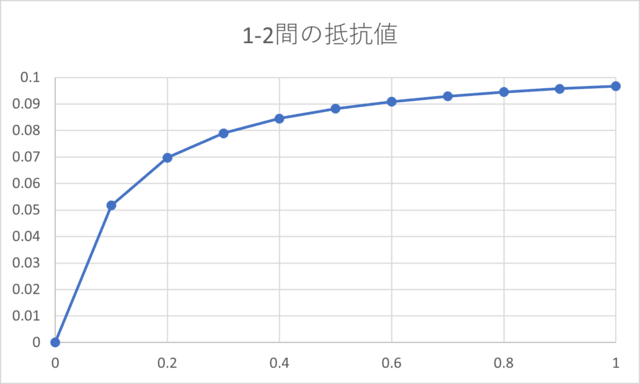
1-2間の抵抗値は、αxR/(α+x)
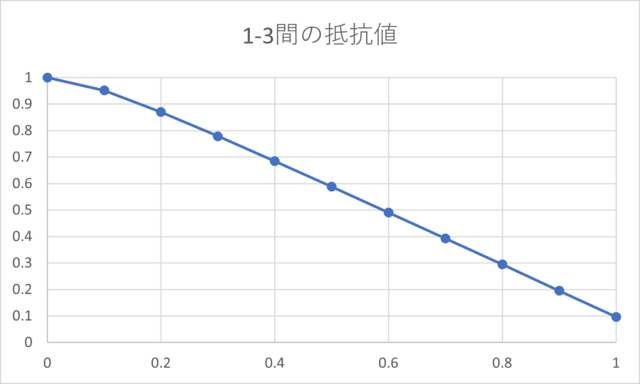
1-3間の抵抗値は、αxR/(α+x) + (1-α)R
1-3間の抵抗値にたいする、1-2間の抵抗値の比率は
{αxR/(α+x)}/{αxR/(α+x) + (1-α)R} = αx/{α+x-α^2}
α=0.5のとき15%になるxは 3/28=0.10714....(疑似15Aカーブ)
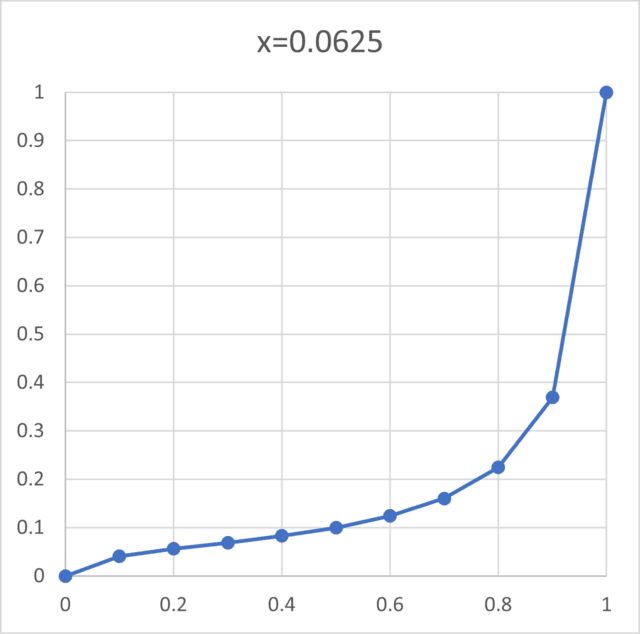
α=0.5のとき10%になるxは 1/16=0.0625 (疑似10Aカーブ)
それぞれをグラフにすると、以下のようになります。
疑似15Aカーブ

疑似10Aカーブ
大事なことなので2回書きますが、あくまでも抵抗値の比率がAカーブになるのであって、抵抗値の変化はAカーブではありません。
電圧の抵抗値分割などには使えますが、電流値の制御には使えません。
ちなみに1-2間の抵抗値、1-3間の抵抗値のカーブはこんな感じ(疑似15Aカーブの場合)
具体的に、150kΩの15Aカーブを作ろうと思ったら、
15%カーブなので、x=3/28
α=1の時の1-3間の抵抗値は、3/28*R/(1+3/28)=3/31*Rなので、
150k=3/31R R=1550kΩ こんな値の可変抵抗器は市販されていないので、1M Ωで代用します。
R=1MΩのとき、α=100%のときの1-3間の抵抗値を150kΩにしようとすると
x /(1+x)=0.15
x= 3/17=0.1764...
つまり、176kΩの抵抗を並列につなぎます。 E24系列なら180kΩですね。
x=0.18
1MΩと180kΩの並列つなぎで、152.54kΩ
1MΩのBカーブ可変抵抗に180kΩの抵抗を並列につないだ時の挙動は以下の通り
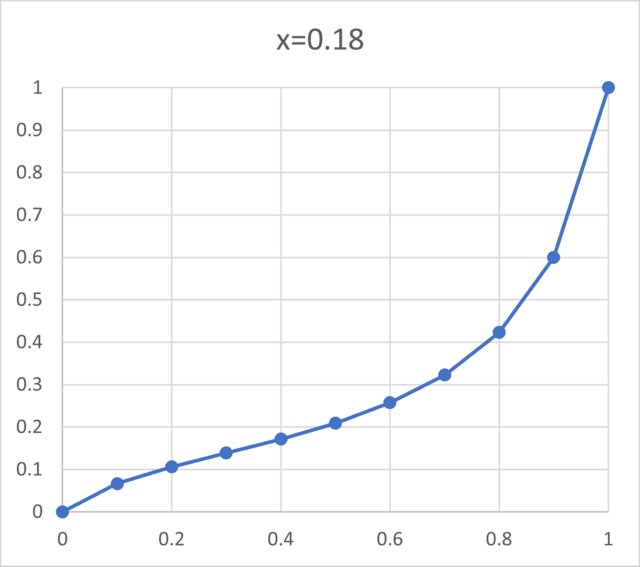
揺動子50%で20%くらいになってしまうけれど、Logっぽいカーブにはなっていますね。
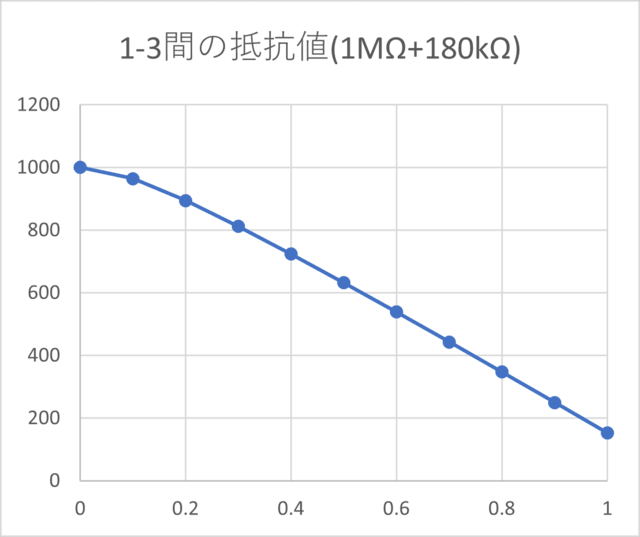
ちなみに、その時の1-2間の抵抗値

おなじく1-3間の抵抗値
参考にした記事は、前回と同じ。
回路図はこれ。

ただ、Cカーブのようにはうまくいかず、悩んだ末、抵抗値としての絶対値ではなく、1-3端子間にたいする1-2端子間の抵抗値の比率がAカーブになる、ということで、理解しました。
1-2間の抵抗値は、αxR/(α+x)
1-3間の抵抗値は、αxR/(α+x) + (1-α)R
1-3間の抵抗値にたいする、1-2間の抵抗値の比率は
{αxR/(α+x)}/{αxR/(α+x) + (1-α)R} = αx/{α+x-α^2}
α=0.5のとき15%になるxは 3/28=0.10714....(疑似15Aカーブ)
α=0.5のとき10%になるxは 1/16=0.0625 (疑似10Aカーブ)
それぞれをグラフにすると、以下のようになります。
疑似15Aカーブ

疑似10Aカーブ

大事なことなので2回書きますが、あくまでも抵抗値の比率がAカーブになるのであって、抵抗値の変化はAカーブではありません。
電圧の抵抗値分割などには使えますが、電流値の制御には使えません。
ちなみに1-2間の抵抗値、1-3間の抵抗値のカーブはこんな感じ(疑似15Aカーブの場合)


具体的に、150kΩの15Aカーブを作ろうと思ったら、
15%カーブなので、x=3/28
α=1の時の1-3間の抵抗値は、3/28*R/(1+3/28)=3/31*Rなので、
150k=3/31R R=1550kΩ こんな値の可変抵抗器は市販されていないので、1M Ωで代用します。
R=1MΩのとき、α=100%のときの1-3間の抵抗値を150kΩにしようとすると
x /(1+x)=0.15
x= 3/17=0.1764...
つまり、176kΩの抵抗を並列につなぎます。 E24系列なら180kΩですね。
x=0.18
1MΩと180kΩの並列つなぎで、152.54kΩ
1MΩのBカーブ可変抵抗に180kΩの抵抗を並列につないだ時の挙動は以下の通り

揺動子50%で20%くらいになってしまうけれど、Logっぽいカーブにはなっていますね。
ちなみに、その時の1-2間の抵抗値

おなじく1-3間の抵抗値




















※コメント投稿者のブログIDはブログ作成者のみに通知されます