
「オイラー入門(シュプリンガー版)」(丸善版)
内容紹介:
オイラー積、オイラー線、オイラー角、オイラーの公式など、今日もその名を冠する業績を多く遺す、18世紀の代表的数学者レオンハルト・オイラー。本書は、オイラー自身が示した36個の証明を取り上げ、親切・丁寧に解説した、オイラーの数学への入門書である。本書では、オイラーが重要な貢献をしたテーマから数論、対数、無限級数、解析的数論、複素数、代数、幾何学、組合せ論に沿って8つの章を設けている。それぞれの章は3つの節からなり、まず「プロローグ」で、オイラー以前に知られていたことが論じられる。続く「オイラー登場」では、オイラーの意図が原論文にしたがって紹介され、最後の「エピローグ」でオイラー以降の数学者がどのように彼のアイディアを展開させていったかが述べられている。オイラーの業績の同時代における意義と、彼以降の数学と数学者に与えた影響が浮き彫りにされる。「略伝」では、サンクト・ペテルブルグなどで活躍した彼の生涯を俯瞰することができる。付録として、今なお未完である『全集』の既刊74巻の内容一覧が付されている。
シュプリンガー版:2004年7月1日、254ページ
丸善版:2012年1月20日、254ページ
著者:
ウィリアム・ダンハム: Wikipediaの英文記事
1947年生まれ。もともとトポロジーの訓練を受けていたが、数学の歴史に興味を持ち、レオンハルト・オイラーを専門とするアメリカの作家。このテーマに関する執筆と教育でいくつかの賞を受賞している。
理数系書籍のレビュー記事は本書で461冊目。
レオンハルト・オイラー(1708-1783)が偉大な数学者であることはもちろん知っていたが、彼の業績の全体像を把握できていなかった。本書はオイラーが開拓した数学全体を解説した格好のオイラー数学入門書である。
高校の数学IIIまできちんと学んでいれば理解できる本だ。学生時代に巡り合えていればどんなによかっただろう。といっても本書はまだ書かれていなかったから無理な話。高校生、大学生にはぜひ読んでほしい。学校で学ぶ数学を超えたところに、オイラー以降の数学の発展に結びつく数々のアイデアと発見があったこと、その広大な領域をたった一人で開拓したという驚異的な偉業を知ることができるはずだ。日本では江戸時代中期のことである。
「オイラーの公式」はあまりにも有名だが、僕が次に興味を持ったのは「無限級数の和の不思議」だった。高校時代に等比数列の和を学んだとき、たいていの学生は Σ1/n の無限和や Σ1/n^2、Σ1/n^3、Σ1/n^4 などの無限和はどうなるのだろうと気になってくるものだ。僕もその一人だった。
Σ1/n^2という「バーゼル問題」を解決したのがオイラーで、1644年に出題され、解決したのは91年後の1735年のこと。簡単そうに見えるこの問題を僕が高校時代に解けなかったのは当然だ。
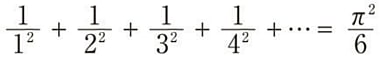
Σ1/n^2、Σ1/n^3、Σ1/n^4 などの無限和の研究は、べき乗の数が負の場合に拡張され、リーマン予想にでてくるゼータ関数の研究に発展していくことになる。たとえばべき乗の数が -1 のときは次のような不思議な結果が得られる。(もちろん、右辺が +∞ も正解だ。)

証明や解説は、以下のページをお読みになるとよい。
ゼータ関数と物理|驚異のウルトラたし算が宇宙を支える
https://club.informatix.co.jp/?p=3702
なぜゼータ関数の自然数の和は無限大に発散しないのか?
https://xseek-qm.net/Euler.htm
自然数の総和がゼータ関数の-1/12であることの新しい証明
https://xseek-qm.net/Regularization.htm
本書の章立ては次の通りだ。
略伝
第1章 オイラーと数論
第2章 オイラーと対数
第3章 オイラーと無限級数
第4章 オイラーと解析的数論
第5章 オイラーと複素数
第6章 オイラーと代数
第7章 オイラーと幾何学
第8章 オイラーと組合せ論
一見して何が書かれているか想像できそうな気がするが、予想をはるかに超える「深い数学」が開設されていた。特に「オイラーと複素数」は、すでに理解している「オイラーの公式」のことだから、大したことが書かれていないのだろうと早合点していたのだが、つまらなそうに思えたこの章がいちばん感動した。
また、幾何学には苦手意識があるため「オイラーと幾何学」は飛ばそうと思ったが、ユークリッド幾何学(特に単なる三角形の幾何がもつ性質であっても)、ユークリッドからオイラーの時代までに発見されていなかった定理があることに衝撃を受けた。
ひとつひとつの章のテーマは、高校数学で学んだ内容の先にある事柄だ。解法のパターンを覚えて解く受験数学を学ぶのに疲れたとき、オイラーが開拓した斬新なアイデア、凡人には思いつけない天才的な解法を知るとまったく新しい世界があることを知ることができる。僕が高校生や大学初年度の学生に本書を勧めたい理由はここにある。
本書には続編がある。といっても同じ著者が書いた本の訳書ではなく、ゼータ関数、リーマン予想の研究の第一人者として知られる数学者黒川信重先生がお書きになった本だ。
「オイラー入門(シュプリンガー版)」(丸善版)
「オイラー探検(シュプリンガー版)」(丸善版)(紹介記事)


翻訳のもとに担った英語版はこちら。
「Euler the Master of Us All: William Dunham」(Amazon.com)

さらに学んでみたい方には、オイラー自身が書いたこちらの2冊をお勧めしたい。
「オイラーの無限解析」
「オイラーの解析幾何」


『オイラー全集(Opera Omnia)』: Amazonで検索
参考: The Euler Archive
http://eulerarchive.maa.org/
関連動画:
著者によるオイラーの数学の紹介動画である。
A Tribute to Euler - William Dunham
Your humble Servant, Is. Newton by William Dunham
YouTubeで著者の動画を: 検索する
関連記事:
オイラー探検:黒川信重
https://blog.goo.ne.jp/ktonegaw/e/b3a7ff7b1a52dac14f08ab40c11471fb




「オイラー入門(シュプリンガー版)」(丸善版)

謝辞
序文
略伝
第1章 オイラーと数論
- プロローグ
- オイラー登場
- エピローグ
第2章 オイラーと対数
- プロローグ
- オイラー登場
- エピローグ
第3章 オイラーと無限級数
- プロローグ
- オイラー登場
- エピローグ
第4章 オイラーと解析的数論
- プロローグ
- オイラー登場
- エピローグ
第5章 オイラーと複素数
- プロローグ
- オイラー登場
- エピローグ
第6章 オイラーと代数
- プロローグ
- オイラー登場
- エピローグ
第7章 オイラーと幾何学
- プロローグ
- オイラー登場
- エピローグ
第8章 オイラーと組合せ論
- プロローグ
- オイラー登場
- エピローグ
内容紹介:
オイラー積、オイラー線、オイラー角、オイラーの公式など、今日もその名を冠する業績を多く遺す、18世紀の代表的数学者レオンハルト・オイラー。本書は、オイラー自身が示した36個の証明を取り上げ、親切・丁寧に解説した、オイラーの数学への入門書である。本書では、オイラーが重要な貢献をしたテーマから数論、対数、無限級数、解析的数論、複素数、代数、幾何学、組合せ論に沿って8つの章を設けている。それぞれの章は3つの節からなり、まず「プロローグ」で、オイラー以前に知られていたことが論じられる。続く「オイラー登場」では、オイラーの意図が原論文にしたがって紹介され、最後の「エピローグ」でオイラー以降の数学者がどのように彼のアイディアを展開させていったかが述べられている。オイラーの業績の同時代における意義と、彼以降の数学と数学者に与えた影響が浮き彫りにされる。「略伝」では、サンクト・ペテルブルグなどで活躍した彼の生涯を俯瞰することができる。付録として、今なお未完である『全集』の既刊74巻の内容一覧が付されている。
シュプリンガー版:2004年7月1日、254ページ
丸善版:2012年1月20日、254ページ
著者:
ウィリアム・ダンハム: Wikipediaの英文記事
1947年生まれ。もともとトポロジーの訓練を受けていたが、数学の歴史に興味を持ち、レオンハルト・オイラーを専門とするアメリカの作家。このテーマに関する執筆と教育でいくつかの賞を受賞している。
理数系書籍のレビュー記事は本書で461冊目。
レオンハルト・オイラー(1708-1783)が偉大な数学者であることはもちろん知っていたが、彼の業績の全体像を把握できていなかった。本書はオイラーが開拓した数学全体を解説した格好のオイラー数学入門書である。
高校の数学IIIまできちんと学んでいれば理解できる本だ。学生時代に巡り合えていればどんなによかっただろう。といっても本書はまだ書かれていなかったから無理な話。高校生、大学生にはぜひ読んでほしい。学校で学ぶ数学を超えたところに、オイラー以降の数学の発展に結びつく数々のアイデアと発見があったこと、その広大な領域をたった一人で開拓したという驚異的な偉業を知ることができるはずだ。日本では江戸時代中期のことである。
「オイラーの公式」はあまりにも有名だが、僕が次に興味を持ったのは「無限級数の和の不思議」だった。高校時代に等比数列の和を学んだとき、たいていの学生は Σ1/n の無限和や Σ1/n^2、Σ1/n^3、Σ1/n^4 などの無限和はどうなるのだろうと気になってくるものだ。僕もその一人だった。
Σ1/n^2という「バーゼル問題」を解決したのがオイラーで、1644年に出題され、解決したのは91年後の1735年のこと。簡単そうに見えるこの問題を僕が高校時代に解けなかったのは当然だ。
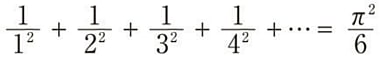
Σ1/n^2、Σ1/n^3、Σ1/n^4 などの無限和の研究は、べき乗の数が負の場合に拡張され、リーマン予想にでてくるゼータ関数の研究に発展していくことになる。たとえばべき乗の数が -1 のときは次のような不思議な結果が得られる。(もちろん、右辺が +∞ も正解だ。)

証明や解説は、以下のページをお読みになるとよい。
ゼータ関数と物理|驚異のウルトラたし算が宇宙を支える
https://club.informatix.co.jp/?p=3702
なぜゼータ関数の自然数の和は無限大に発散しないのか?
https://xseek-qm.net/Euler.htm
自然数の総和がゼータ関数の-1/12であることの新しい証明
https://xseek-qm.net/Regularization.htm
本書の章立ては次の通りだ。
略伝
第1章 オイラーと数論
第2章 オイラーと対数
第3章 オイラーと無限級数
第4章 オイラーと解析的数論
第5章 オイラーと複素数
第6章 オイラーと代数
第7章 オイラーと幾何学
第8章 オイラーと組合せ論
一見して何が書かれているか想像できそうな気がするが、予想をはるかに超える「深い数学」が開設されていた。特に「オイラーと複素数」は、すでに理解している「オイラーの公式」のことだから、大したことが書かれていないのだろうと早合点していたのだが、つまらなそうに思えたこの章がいちばん感動した。
また、幾何学には苦手意識があるため「オイラーと幾何学」は飛ばそうと思ったが、ユークリッド幾何学(特に単なる三角形の幾何がもつ性質であっても)、ユークリッドからオイラーの時代までに発見されていなかった定理があることに衝撃を受けた。
ひとつひとつの章のテーマは、高校数学で学んだ内容の先にある事柄だ。解法のパターンを覚えて解く受験数学を学ぶのに疲れたとき、オイラーが開拓した斬新なアイデア、凡人には思いつけない天才的な解法を知るとまったく新しい世界があることを知ることができる。僕が高校生や大学初年度の学生に本書を勧めたい理由はここにある。
本書には続編がある。といっても同じ著者が書いた本の訳書ではなく、ゼータ関数、リーマン予想の研究の第一人者として知られる数学者黒川信重先生がお書きになった本だ。
「オイラー入門(シュプリンガー版)」(丸善版)
「オイラー探検(シュプリンガー版)」(丸善版)(紹介記事)


翻訳のもとに担った英語版はこちら。
「Euler the Master of Us All: William Dunham」(Amazon.com)

さらに学んでみたい方には、オイラー自身が書いたこちらの2冊をお勧めしたい。
「オイラーの無限解析」
「オイラーの解析幾何」


『オイラー全集(Opera Omnia)』: Amazonで検索
参考: The Euler Archive
http://eulerarchive.maa.org/
関連動画:
著者によるオイラーの数学の紹介動画である。
A Tribute to Euler - William Dunham
Your humble Servant, Is. Newton by William Dunham
YouTubeで著者の動画を: 検索する
関連記事:
オイラー探検:黒川信重
https://blog.goo.ne.jp/ktonegaw/e/b3a7ff7b1a52dac14f08ab40c11471fb




「オイラー入門(シュプリンガー版)」(丸善版)

謝辞
序文
略伝
第1章 オイラーと数論
- プロローグ
- オイラー登場
- エピローグ
第2章 オイラーと対数
- プロローグ
- オイラー登場
- エピローグ
第3章 オイラーと無限級数
- プロローグ
- オイラー登場
- エピローグ
第4章 オイラーと解析的数論
- プロローグ
- オイラー登場
- エピローグ
第5章 オイラーと複素数
- プロローグ
- オイラー登場
- エピローグ
第6章 オイラーと代数
- プロローグ
- オイラー登場
- エピローグ
第7章 オイラーと幾何学
- プロローグ
- オイラー登場
- エピローグ
第8章 オイラーと組合せ論
- プロローグ
- オイラー登場
- エピローグ






















