

こんにちは、四谷大塚NETフォーラム塾上本町教室塾長・学びスタジオ代表の奧川えつひろです。
ご訪問いただき、ありがとうございます。
今回は、変わる中学受験の算数についてかきます。
❤︎算数・数学の学習過程の概念図は"グルグルの図"
ご訪問いただき、ありがとうございます。
今回は、変わる中学受験の算数についてかきます。
❤︎算数・数学の学習過程の概念図は"グルグルの図"
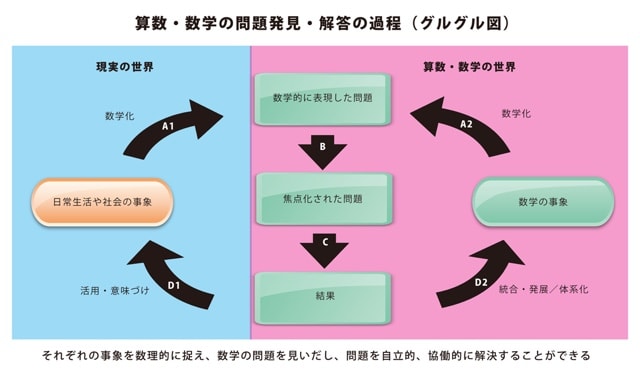
このグルグル図、算数・数学の学習過程で示されているのは、
「何のために数学を学ぶのか」
という根源的な問いです。
❤︎"算数・数学の問題"は、普通は"真ん中"の部分
普通に思い浮かべる"算数・数学の問題"というのは、上の図の真ん中の部分です。
つまり、
"数学的に表現した問題"とは、
教科書や問題集に載っている定型的な問題です。
算数で言えば"○○算"の形、
数学で言えば"方程式"を取り出すのが、
"焦点化した問題"に向かう矢印Bの部分です。
知識や解法を使って"結果"を導き出す矢印Cの部分が、
パターン通りの処理になります。
このような流れが、
多くの方が持っている「算数・数学の問題」を解くことだと思います。
❤︎共通テストでは、この"真ん中"の流れに至る"前"の部分が問われている
図の左側"現実の世界"は、
"日常生活や社会の事象"から数学的な事象を取り出すという観点からの問いかけです。
"数学の問題にたどり着くまでが長い"というのは、
この青い矢印"D1""A1"の部分が長いからです。
現実の世界では、
実際に起こっていることがらを数理的に捉え、
数学的に処理し、
問題を解決することが求められます。
"算数・数学にたどり着くまでの部分"も、
"数学的活動"だと捉えており、
その部分に対応する力を、
数学を通じて身につける必要があります。
❤︎解法パターンが通用しない入試
これまで大学入試は、
処理能力や知識が問われていた。
しかし、
近年の入試問題は違います。
具体的な事象から法則を見つけ、
その取り出した法則を使って、
次の具体的な問題を解決していく、
といった場面が多く設定されています。
単なる処理能力から、
新しい課題を解決するための思考能力
を問うように変化しています。
❤︎実際の中学入試の問題の傾向
実際、中学の入試問題を見ると、
算数・数学で求められる力を反映させた問題が増えてきています。
将来大学入試で求められる資質・能力を念頭において
中学入試問題を作成されています。
❶読解力が問われる
「○○算」といった解法や、
計算技術に加えて、
そこに書いてある文の意味を読み取り、
それに従って作業できるか、
つまり
"読解力"が問われています。
具体的な対象をよく観察し、
そこに存在するルールを見つけ出して解決して行かなければなりません。
❷質問の意味を理解できているか
また、
問題に対して、
この問いの状況を「それってどういうこと?」と問い直して言い換えることができることも必要です。
この"言い換え"をする力は、
数学で非常に重要です。
それは、
本質をつかみ出す能力だからです。
❸その場で問題に向き合って考え抜く姿勢があるか
与えられたものをしっかり受け止め、
たとえば、問題の中に書かれている図などをヒントにして、
"その場で読み取って考え、手を動かして試すことをいとわない"ことが求められています。
❹過程をしっかりたどる力
まず、
問題文の提示している状況の理解ができるかどうかが初めの壁になります。
具体例を参照しながら、
ルールを読解します。
問いの並びに従って、
1つの問題の答えを
次の問題の解決の手がかりとして振り返ることができるような力を問われます。
この数学で要求される"過程をしっかりたどる力"は、
今後の学問や仕事で求められる力につながります。
❺問いが次のヒントに
問題によっては、
問いが次のヒントになっていることに
気付けるかが、
分かれ目になる問題もあります。
❻説明が求められる
説明を求められる問題が出題されます。
このような"説明"は、
中学以降の数学では"証明"として求められる作業です。
数学では結果が言えるだけでなく、
その"途中"が"つなげられるか"が重要です。
そういった姿勢を持っているかを問われます。
❤︎まとめ。変わる中学受験の算数
「○○算」といった解法に加え、
❶読解力があるか
❷質問の意味を理解できているか
❸その場で問題に向き合って考え抜く姿勢があるか
❹過程をしっかりたどる力があるか
❺問いが次のヒントにできるか
❻説明できるか
これらは、大学受験や社会につながります。
「何のために数学を学ぶのか」
という根源的な問いです。
❤︎"算数・数学の問題"は、普通は"真ん中"の部分
普通に思い浮かべる"算数・数学の問題"というのは、上の図の真ん中の部分です。
つまり、
"数学的に表現した問題"とは、
教科書や問題集に載っている定型的な問題です。
算数で言えば"○○算"の形、
数学で言えば"方程式"を取り出すのが、
"焦点化した問題"に向かう矢印Bの部分です。
知識や解法を使って"結果"を導き出す矢印Cの部分が、
パターン通りの処理になります。
このような流れが、
多くの方が持っている「算数・数学の問題」を解くことだと思います。
❤︎共通テストでは、この"真ん中"の流れに至る"前"の部分が問われている
図の左側"現実の世界"は、
"日常生活や社会の事象"から数学的な事象を取り出すという観点からの問いかけです。
"数学の問題にたどり着くまでが長い"というのは、
この青い矢印"D1""A1"の部分が長いからです。
現実の世界では、
実際に起こっていることがらを数理的に捉え、
数学的に処理し、
問題を解決することが求められます。
"算数・数学にたどり着くまでの部分"も、
"数学的活動"だと捉えており、
その部分に対応する力を、
数学を通じて身につける必要があります。
❤︎解法パターンが通用しない入試
これまで大学入試は、
処理能力や知識が問われていた。
しかし、
近年の入試問題は違います。
具体的な事象から法則を見つけ、
その取り出した法則を使って、
次の具体的な問題を解決していく、
といった場面が多く設定されています。
単なる処理能力から、
新しい課題を解決するための思考能力
を問うように変化しています。
❤︎実際の中学入試の問題の傾向
実際、中学の入試問題を見ると、
算数・数学で求められる力を反映させた問題が増えてきています。
将来大学入試で求められる資質・能力を念頭において
中学入試問題を作成されています。
❶読解力が問われる
「○○算」といった解法や、
計算技術に加えて、
そこに書いてある文の意味を読み取り、
それに従って作業できるか、
つまり
"読解力"が問われています。
具体的な対象をよく観察し、
そこに存在するルールを見つけ出して解決して行かなければなりません。
❷質問の意味を理解できているか
また、
問題に対して、
この問いの状況を「それってどういうこと?」と問い直して言い換えることができることも必要です。
この"言い換え"をする力は、
数学で非常に重要です。
それは、
本質をつかみ出す能力だからです。
❸その場で問題に向き合って考え抜く姿勢があるか
与えられたものをしっかり受け止め、
たとえば、問題の中に書かれている図などをヒントにして、
"その場で読み取って考え、手を動かして試すことをいとわない"ことが求められています。
❹過程をしっかりたどる力
まず、
問題文の提示している状況の理解ができるかどうかが初めの壁になります。
具体例を参照しながら、
ルールを読解します。
問いの並びに従って、
1つの問題の答えを
次の問題の解決の手がかりとして振り返ることができるような力を問われます。
この数学で要求される"過程をしっかりたどる力"は、
今後の学問や仕事で求められる力につながります。
❺問いが次のヒントに
問題によっては、
問いが次のヒントになっていることに
気付けるかが、
分かれ目になる問題もあります。
❻説明が求められる
説明を求められる問題が出題されます。
このような"説明"は、
中学以降の数学では"証明"として求められる作業です。
数学では結果が言えるだけでなく、
その"途中"が"つなげられるか"が重要です。
そういった姿勢を持っているかを問われます。
❤︎まとめ。変わる中学受験の算数
「○○算」といった解法に加え、
❶読解力があるか
❷質問の意味を理解できているか
❸その場で問題に向き合って考え抜く姿勢があるか
❹過程をしっかりたどる力があるか
❺問いが次のヒントにできるか
❻説明できるか
これらは、大学受験や社会につながります。




















1−1=?から、ゼロの概念の違いがありますね。