SCILABによる制御系設計 その１０

Scilab 10
根軌跡の続き
Ht=(s+2)^2/(s^2+4)/(s+5)^2;
-->H=syslin('c',Ht);
-->evans(H,100);
-->sgrid
とすることで　このような極座標グリッド線が入ったグラフがかける
これはMATLABとほぼ同じ
ただし、デフォルトの色がなあ　ちょっと見にくい


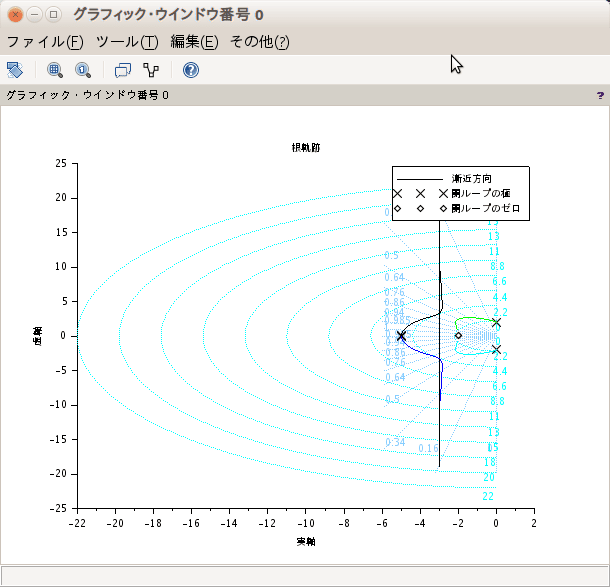
尾形先生のprogram４−１０などにより、減衰ζ=0.5 と0.707の放射線と
ω=0.5、1,2のみの円を示したれば

>sgrid([0.5,0.707],[0.5,1.2]);
でこうなる。
ζ：減衰は複素平面上で角度φの角度を持った放射線になる。またωは一定半径の円となります。


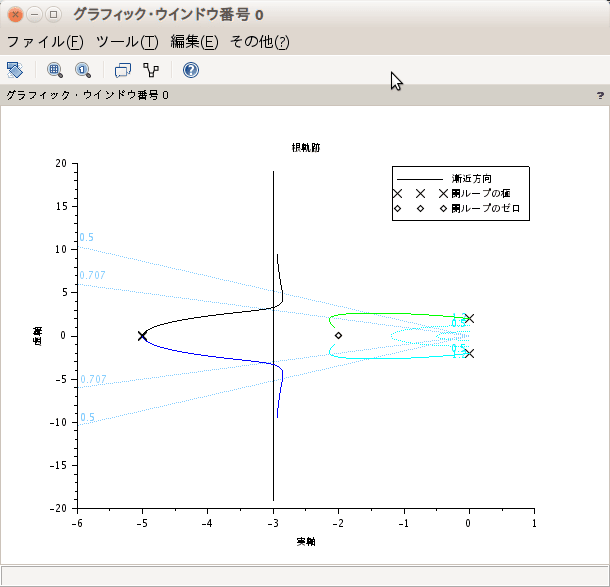
ちょっといびつ

SCILABによる制御系設計 その9

Scilab 9
4章　は　根軌跡解析

根軌跡解析は制御系の特性を理解する上で重要であるが、小職はなんとなく飛ばしてきた。ので、その反省を踏まえ整理していきたい。
前回までは、過渡応答解析によって、システムの振る舞いを時系列のデータとして、例えばステップ応答などによって視覚的に確認することを行ってきた。感覚的にはこれで、システムの特性がわかるようになったのであるが、それだけだと、制御系設計するときには、感覚的になってしまう。
システムの特性を捉えて、よりよい制御系を設計するために、零点と極というものを考えていくことが必要？になる。
まあ、勉強してみましょう。
-->s=poly(0,'s')
-->Ht=(s+3)/(s*(s+1)*(s^2+4*s+16));
-->H=syslin('c',Ht);
として　コマンドevansによって
-->evans(H,100);
１００はゲインの最大値。これは何をしているかというと、システムHに対して、一巡伝達関数がゲインKによっての根軌跡を表示する。
ゲインを上げていくと、制御系は場合によって不安定になる。

それをみていくことになる。

SCILABによる制御系設計 その８

Scilab8
３　過渡応答解析 （その5）

初期条件を与えた場合の応答

-->t=0:0.05:10;

-->A=[0 1 0;0 0 1;-10 -17 -8];

-->B=[0;0;0];

-->C=[1 0 0];

-->D=[0];

状態空間表現で

-->x0=[2;1;0.5];

初期状態ベクトルをこのようにする

-->E=[1 0 0;0 1 0;0 0 1];
これをいつも忘れる

-->u=zeros(1,201);
入力はなし

-->plot2d(csim(u,t,des2ss(A,B,C,D,E),x0));
警告: csim: 入力引数 #1 は連続時間系で指定してください.

ということで


となる
尾形先生のprogram 3-36参照
matlabではinitialというコマンドを使うが
scilabでは一貫してcsimでいける


さらに過渡応答のところで　例題３−２５では３次元プロットをしている。
例えばscilabでは
減衰を６種類変えて　３次元のプロットは。
matlabだとmeshというのでいけるのですが
scilabは　例えば次のようにしました

>for n=1:6
-->sy=1/(s^2+2*(n-1)*0.2*s+1);
-->y(n,:)=csim('step',t,tf2ss(sy));
-->end

->nn=[1 2 3 4 5 6];
-->plot3d(nn',t',y);
で

ちょっと色がきたないかな

SCILABによる制御系設計 その7

Scilab7
３　過渡応答解析 （その4）

インパルス応答をやってみよう

plot2d([t',t'],[(csim('impulse',t,des2ss(A,B,C,D,E)))',0*t'])

でいけるはず。

-->A=[0 1;-1 -1];

-->B=[0;1];

-->C=[1 0];

-->D=[0];

-->E=[1 0;0 1];

-->t=0:0.01:10;

-->plot2d([t',t'],[(csim('impuls',t,des2ss(A,B,C,D,E)))',0*t'])
警告: csim: 入力引数 #1 は連続時間系で指定してください.

で


任意の入力の場合、


s=poly(0,'s');

-->sy=5/(s^2+s+5);

として

-→u=2+t;

つまりランプ入力

plot2d(csim(u,t,tf2ss(sy)));

とすれば任意の入力uに対する応答が得られる。

SCILABによる制御系設計 その7

Scilab7
３　過渡応答解析 （その4）

インパルス応答をやってみよう

plot2d([t',t'],[(csim('impulse',t,des2ss(A,B,C,D,E)))',0*t'])

でいけるはず。

-->A=[0 1;-1 -1];

-->B=[0;1];

-->C=[1 0];

-->D=[0];

-->E=[1 0;0 1];

-->t=0:0.01:10;

-->plot2d([t',t'],[(csim('impuls',t,des2ss(A,B,C,D,E)))',0*t'])
警告: csim: 入力引数 #1 は連続時間系で指定してください.

で


任意の入力の場合、


s=poly(0,'s');

-->sy=5/(s^2+s+5);

として

-→u=2+t;

つまりランプ入力

plot2d(csim(u,t,tf2ss(sy)));

とすれば任意の入力uに対する応答が得られる。