SCILABによる制御系設計 その6

Scilab6
３　過渡応答解析 （その２）

尾形先生の本は、過渡応答解析について例題がたくさんある。
前回のシステムに加え、さらに高次のシステム、伝達関数表現ではなく、
状態空間表現でのステップ応答などやフィードバックがある場合など豊富に解説している。

さて、その中で一つやってみよう。
２入力２出力の状態空間表現では、４つの伝達関数があり、４つの応答がそれぞれ得られる。

-->plot2d([t',t'],[(csim('step',t,des2ss(A,B,C,D,E)))',0*t'])
警告: csim: 入力引数 #1 は連続時間系で指定してください.
!--error 10000
csim: 入力引数 #1 の型が間違っています: SIMOを指定してください.
at line 57 of function csim called by :
plot2d([t',t'],[(csim('step',t,des2ss(A,B,C,D,E)))',0*t'])

そうなのか、csimは１入力なのですね。
matlabの場合、step(A,B,C,D)で４つのグラフができる。
うーん、これはmatlabに軍配か！

では
-->tt=ss2tf(Sc);

-->tt
tt =

- 1 + s - 1.776D-15 + s
----------- -------------
2 2
6.5 + s + s 6.5 + s + s

7.5 + s 6.5
----------- -----------
2 2
6.5 + s + s 6.5 + s + s

として、４つの伝達関数としてあげて
ひとつひとつ
for i=1:2
for j=1:2
plot2d([t',t'],[(csim('step',t,tf2ss(tt(i,j))))',0*t']);
end;end;



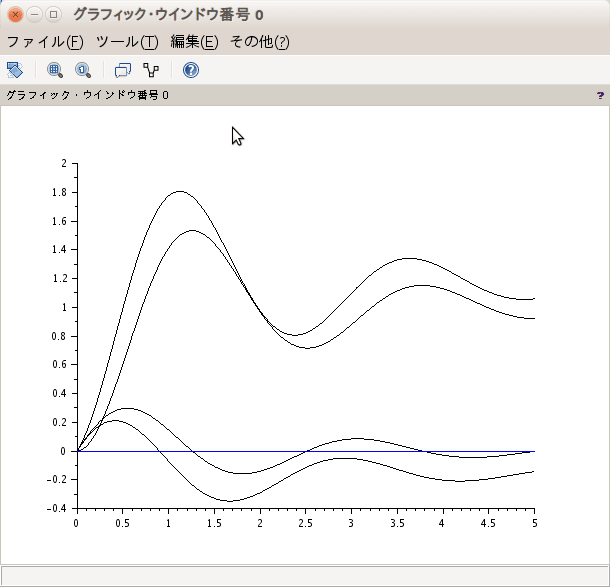
ははは　出来た
でも、色がおなじか
まあ、ループの中に色を変えるコマンドを入れれば良いかな

matlabは小さいウインドで４つできるが

まあ、今日はここまで

SCILABによる制御系設計 その5

３　過渡応答解析

過渡応答解析の目的は、システムの特性を時間軸で見ることである。

はじめにステップ応答について見てみる。


scilabでは過渡応答はcsimで簡単にできる。パラメータを’step’と指定するとステップ応答となる。




->t=0:0.05:5;

-->s=poly(0,'s');

-→S1=(2*s+10)/(s^2+2*s+10);


-->plot2d([t',t'],[(csim('step',t,tf2ss(S1)))',0*t'])
警告: csim: 入力引数 #1 は連続時間系で指定してください.

あれ、警告だ。ちょっと例題どおりなのに（ヘルプの）
今度調べます。

さて伝達関数は尾形先生の例題３−１のバネマスダッシュポット系です。


2次系のステップ応答の典型ですね。グラフのテクニックは別途勉強が必要ですね

MATLAB関連の書籍 ブレイク

MATLAB関連書籍では

基礎はこれですが

	MATLABによる制御理論の基礎
	クリエーター情報なし
	東京電機大学出版局

やはり　これがベストセラーでしょう

	MATLABによる制御系設計
	野波 健蔵,平田 光男,西村 秀和
	東京電機大学出版局

かなりこれにはお世話になっております。H∞、スライディングモードなどの構築方法が例題やベンチマークモデルと共に解説されています。

SCILABによる制御系設計 その4

Scilab4
２　動的解析の準備　の続き その２

ブロック線図はシステムの表現としては非常にわかりやすい。

左から
入力を→で示し、システムは下記のようになる



そしてフィードバックは




これが複数あった場合、直列や並列につなげた場合、全体をシステムとして
演算したらどうなるか。
または、フィードバックシステムを表現したらどうなるか
ということをやってみる。




こんなかんじ。直列が＊　並列が＋　フィードバックが/.の演算子でOK。

SCILABによる制御系設計 その3

２　動的解析の準備　の続き

前回、伝達関数と状態空間表示の変換についてやってみた。

伝達関数はラプラス演算子sによる記述であり、状態空間も状態量ｘ（ｔ）による表現であった。
連続時間での表現であった。

前回は、伝達関数→状態空間の変換までやってきた。
今回は状態空間→伝達関数の変換をやってみる。
-->A=[0 1 0;0 0 1;-5.008 -25.1026 -5.03247];

-->B=[0;25.04;-121.005];

-->C=[1 0 0];

-->D=[0];

-->E=[1 0 0;0 1 0;0 0 1];
として
-->S=des2ss(A,B,C,D,E);

-->H=ss2tf(S);

-->H
H =

2
5.0080488 + 25.04s - 5.329D-15s
-------------------------------
2 3
5.008 + 25.1026s + 5.03247s + s


となる。尾形先生の参考書Matlab Program 2-6と同じになったので　まあOKですね。（ならなかったら問題）
さて、これは１入力１出力なので、伝達関数は１つであるが、多入力だった場合はどうするのか？
->A={0 1;-2 -3];

-->B=[1 0;0 1];

-->C=[1 0];

-->D=[0 0];

-->E=[1 0 ;0 1];

-->S=des2ss(A,B,C,D,E);

-->H=ss2tf(S);

-->H
H =

3 + s 1
--------- ---------
2 2
2 + 3s + s 2 + 3s + s
となり、特に意識しないでも２つでる。（Matlabの場合指定するが）


連続系はここまでで、システムの場合、離散系も考えられる。変換はMatlabではc2dであるが、scilabではdscrらしいが引数がシステムである。まあ、やってみよう。

-->A=[0 1;-25 -4];
--→B=[0;1];
だけではシステムとして定義できないのでCを追加
-->C=[1 0];

-->Si=syslin('c',A,B,C);

-->sld=dscr(Si,0.05)　サンプリング0.05で離散化
sld =


sld(1) (state-space system:)

!lss A B C D X0 dt !

sld(2) = A matrix =

0.9708833 0.0448470
- 1.1211761 0.7914951

sld(3) = B matrix =

0.0011647
0.0448470

sld(4) = C matrix =

1. 0.

sld(5) = D matrix =

0.

sld(6) = X0 (initial state) =

0.
0.

sld(7) = Time domain =

0.05

となった。これも尾形先生の参考書Program2-9と同じ結果。ただし、精度には注意（format long )とMatlabでは参考書に書いてありましたが、scilabの場合はこのままで精度は良いようです。