7月22日皆既日食～日食特集第3部

引き続き、7月22日の日食特集です。
あえて部分日食の楽しみ方ということで、月の大きさを測る方法について紹介しています。

第3部では、第2部で求めた月の大きさに太陽の角度を加味して、より実際の大きさに近い値を求めます。


９．太陽の角度を測る

まず、自分が観測する場所から見た、トカラ列島の方角を地図で調べましょう。
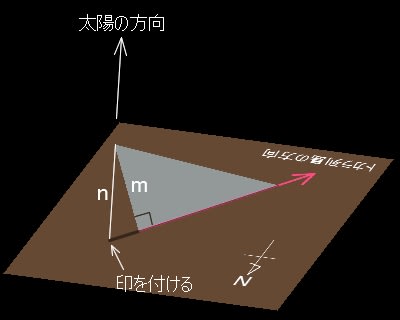
そして、厚紙または板の上に、東西南北の方向と、トカラ列島の方角を下の図のように描いておきましょう。
矢印は大きめに描いて下さい。



この矢印に沿って、下の図のように三角定規を立てます。
角度が垂直であれば、三角定規以外のもの（長方形のもの等）でも構いません。
ただし、角がちゃんと尖ったものを使って下さい。
三角定規を立てると図のように影ができます。



三角定規を、1辺を矢印に固定したまま（セロハンテープ等で固定するといいでしょう）ゆっくり倒していきます。
ある角度まで倒すと、下の図のように影が直線状になるはずです。
このとき、影の先端に印を付けます。
そして、三角定規の高さmと、印から三角定規の頂点までの距離nを測っておきましょう。



１０．太陽の角度を加味して月の大きさを測る

下の図のように、太陽が斜めから照っているとき、影の大きさ（影から計算された大きさ）Kは月の実際の大きさLよりも大きくなります。
一方、９で測定したmとnを使って、次のような関係が成り立ちます。
m : n = L : K
これは三角形の相似を使って簡単に分かりますので、考えてみて下さい。
つまり、実際の月の大きさLは、第2部で計算した大きさKの、m/n倍となります。
当然m＜nですから、実際の月の大きさは、第2部で計算した値より小さくなります。




１１．まとめ

では、まとめです。
実際の月の大きさの測り方をもう一度おさらいしておきましょう。

まず、事前に地図上で、トカラ列島（実際には奄美大島北端または種子島南端）までの距離を測っておきます。
また、方角も測って、９で説明したように紙や板に描いておきます。

当日、トカラで皆既日食が起こる10:56頃に、７の図を参考にしながら部分日食の食分を調べます。

それと同時に、事前に用意したトカラの方角を描いた紙または板と三角定規を使って、９で説明したように太陽の角度を調べ、mとnの長さを測ります。

観測地からトカラまでの距離をD km、食分をaとすると、月の大きさは、
D ÷ ( 1 － a ) × n ÷ m
すなわち
Dn/(1-a)m
となります。

うまくいけば、3500km前後の値が出るはずです。
くれぐれも事前に地図を使った準備を忘れないこと。
後は晴れるのを祈るばかりですね！