前回の問題に出てきました図に、補助線を引きますと
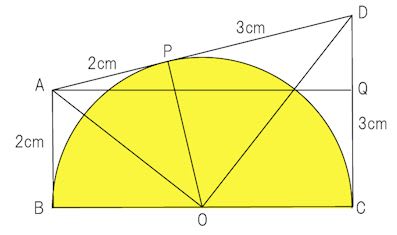
このようになります。
Pは、接点。Qは AQ//BCとなるように引いた線とDCとの交点
△DPOと △DCO は、どちらも直角三角形で
DP DC は接線ですからDOは ∠PDCの角の2等分線
という条件から1組の辺とその両端の角がそれぞれ等しいので
△DPOと △DCOは 相似です。よってDP=DC=3cm
同じように、△APO と △ABO も相似なので
AP=AB=2cm
これより AD=AP+PD=2+3=5 答え 5cm です!
∠AODは、相似な三角形が2組あることから
∠AOB=∠AOP=X
∠DOP=∠DOC=Y としますと
2X+2Y=180 ∠AOD=X+Y=180÷2=90 答え90°
ここで次によく出ますのは、円の半径を求めよという問題!
このときに使うのが三平方の定理です。
直角三角形AQDにおいて
ADの2乗=AQの2乗+DQの2乗
ここに数値を代入しますと
5×5=AQの2乗+1×1
これよりAQ=√24=2√6 これは直径ですから 半径は √6 になります。
これらはセットで覚えておいてください~
きっと役にたちます!









