変形させても、同じものは 同じ！ の術～

昨日は、ここ道北の街にも強い風が吹いていましたが

それ以上荒れることもなく、このあたりは平穏無事でした。

でも、明日はどうなるか分からない日本列島

 

前回の問題は、

下の図は、正六角形の中に ひし形をかいたものです。

色の付いた部分の面積が１３㎠ のとき、

ひし形の面積は 何㎠ ですか？

でした。

 

ここで、面積の計算をしないで  ひし形の白い部分の面積と

色の付いた青い部分の面積を比べてみて  その比を 考えます。

青い部分は三角形が４つです。

そのうちの １つを、面積を変えずに変形させてみます。

三角形は底辺と高さが同じだと 面積は同じなので

図のように赤い線を引いて、

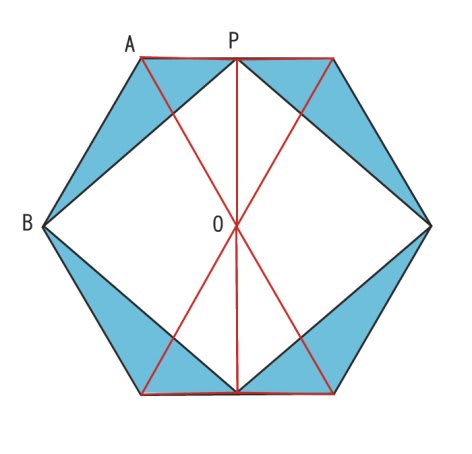
△ABP を △AOP に変形させます。

他の３つの三角形も 同じように変形させますと

このようになります。

正六角形という図形は、中に正三角形が６個入ります。

そのうちの２個が、青い部分になりますので

白い部分（ひし形と同じ面積）は、青い部分の２倍です。

青い部分の面積が１３㎠でしたから、ひし形の面積はその２倍で

答え ２６㎠

 

このように、面積を変えずにカタチを変形させていく術を

等積移動  とか  等積変形   などと言います。

 

大人になりますと、

あまったお肉をこちらに等積移動したい～などと考えるのですが

そう言いながら 何かをポリポリ食べていたのでは・・・・・ムリ！