ちなみにこの時の原子核は高速に近いスピードで走っているため、特殊相対論によるローレンツ収縮により、 進行方向に長さが1/γに縮み(γ = 1/sqrt(1-(v/c)^2)、薄い円盤状になっています。
http://alice-j.org/クォーク・グルーオンプラズマ-qgp/
物が収縮するのはローレンツ収縮ですが、特殊相対論によるローレンツ収縮なら、時空が進行方向に収縮するので、どちらにしても観測者からみて、他の物との距離は変化せず、時空だけが収縮していえるのはありえないので、上の収縮は間違ってますよね?
ーーーーーーーーーーーーーーーーーーーーーーーーー
古典的な意味において、大きさのある時計と、大きさのない座標点を、観測に合うように結び付ける座標系の一つに時空一体にみる座標系がある。
1、そういう意味では、ニュートン力学の絶対静止座標系もその一つ
2、その絶対静止座標系において、物が進行方向にだけ縮むと考えたローレンツが考えたのが、ローレンツ変換
3、そのローレンツ変換は同じだけど、絶対静止座標系を廃して、物ではなく、時空の方が変化すると考えたのがアインシュタイン
https://blog.goo.ne.jp/s_hyama/e/9f92b7bc5cf7e4ad4fd1ce6f7a008a87
下の表は、ニュートン力学~アインシュタインの相対論までまとめたものですが、その認識は合ってますか?
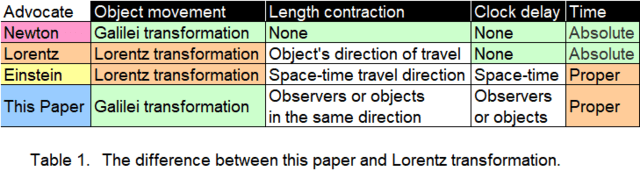
合ってるなら、進行方向に時空が収縮するのが特殊相対論で、物が収縮するのはローレンツの理論で合ってますか?
合ってるなら、特殊相対論で物が収縮するのは、進行方向に時空が収縮するからで、そうすると観測者に物が収縮してみえるということは、進行方向の時空も収縮してみえないとおかしいですよね?
このローレンツ収縮パラドックスによく似たパラドックスに
7.5 ガレージのパラドックス
(余談) 特殊相対論は物理学科では一年生で習う初等科目です。しかし文系や高卒の人が理解す るのは少々難しいでしょう。
https://amonphys.web.fc2.com/amonsr.pdf#search=% …
がありますが、トンデモさんなのは、むしろそのような説明している人たちで
ローレンツのローレンツ収縮のことをいってるのか、アインシュタインの特殊相対論のことを言ってるのか、混在して説明して、わかった気になってるだけではありませんか?









