クイックソートと二分探索木生成

さて、前回、平衡二分探索木の中でもオーソドックスで特に高速なAVL Treeモジュールの使い方を学んだ。

しかしながら、Lispに慣れた層も始めたばかりの層も「ちと気持ち悪い」って思ったんじゃないか。

通常、Lispを使う際はリストばっか相手にしている。そしてリストは「中身が良く見える」。

従って「今何を行って何を作ってるんだろう」と言う過程と結果は一目瞭然だ。

反面、構造体なんかが出てくると「中身が隠蔽されている」為、一体何が起こってるのかが良く分からない。結果だけ出ても「計算が正しいのか否か」、そのプロセスを想像するのが極めて難しくなる(※1)。

そこでここでは、実用性はさておき、リストを使って二分探索木を構築する方法を考えてみよう。

なお、ここで扱うのは平衡二分探索木ではなく、単なる二分探索木だ。

つまり、データ追加を行った際に「自動で」木を生成しなおす事はない(もちろんそういう機能を組み込もうと思えば組み込めるだろうが)。

あくまで二分探索木を「可視化」してその「木の構成」を眺め学ぶのが目的だ。

ところで、ネットなんかで検索してみると、とにかく「木」と言えば構造体、と言うような紹介記事が多い。

しかし、ここは勘違いして欲しくない。「木」自体と「実装方法」は全く関係がないんだ。

理論的な「木」の解説と、実務上「どう実装するか」ってのは全く別の話であり、この２つは原理的に結びついてるわけじゃないんだ。

結果、「木」を解説したいのか「実装法」を解説したいのか意味が分からなくなる。

「理論」と「実践」は分けて考えるべきなんだけど、あいにく、知ってる限り、コンピュータサイエンス系の話だとこのテの話はゴッチャになってる。そして「理論」と「実践」を分けて考えられない、と言う事は「理論的ではない」と言う事だ。

事実、前回やってみせたが、二分探索木は手作業で、Lispだったらリストを使って作る事が可能だ。いや、効率・非効率の話は置いておいて、だ。

そしてPythonやRubyなんかでも「二分探索木」を実験する程度なら組み込みのリスト(Rubyなら配列)を使えば人力で書ける、と言う事だ。使えるデータ型ならそのまま使って構わん、って事である。実験段階で構造体の出番なんてあり得ない。

要するに、Lisp使いは特に、最初に何らかのアイディアを試す、なんてなったらまずはリストを使ってモックアップを作っちゃうんだよな。二分探索木ならリストを使って「理論通りに動くのか」まずはそれを試す。上手く行ったら「最適化」はその後の話、なんだよ。

これはPythonやRubyでも覚えておいた方がいい。と言うか、インタプリタを使った開発のポイントだ。まずは非効率でもいいから「自由度が高い」データ型、おそらく殆どはリストだろう、を使って取り敢えず「動くモノ」を作って理論通りに動くかどうか試してみる。上手く行ったらそこではじめて最適化を考える、ってこった。

Pythonなんかでも二分探索木を作るのに最初からわざわざクラスなんぞ作ってドツボにハマる必要はない(笑)。ハマるだろ(笑)?そうじゃなくって、テキトーにリストを扱いながら関数で「上手く動くもの」を作るんだ。それで「動くためのロジック」がハッキリ書き上がった時点でクラスを・・・ってやった方が紛れがねぇだろう。

最初っからトっぽい「(クラスを使った)自作データ型設計」をしよう、なんてするから大体失敗するんだよ(笑)。

さて、基本に戻る。

二分探索木を習ってまずは意味不明なのが、あまりにも恣意的な「木」を提示されて、言ってるこたぁ分かるんだけど、なんでこの例なんだ?ってピンと来ない辺りなんだよな。

例えば上の図は、最小が1、最大が14の9つの節を持つ二分探索木だ。しかし、なんか「わざとらしい」(笑)。恣意的な匂いがどっかプンプンとしないだろうか(笑)。

そもそも、数値に抜けがある、ってのもなんだかな、とか思う。

そこで、ここでは1から15までの整数の連番で考えてみよう。

1から15までの整数のリストが与えられた時、形成出来る二分探索木に、例えばこんなモノがある。

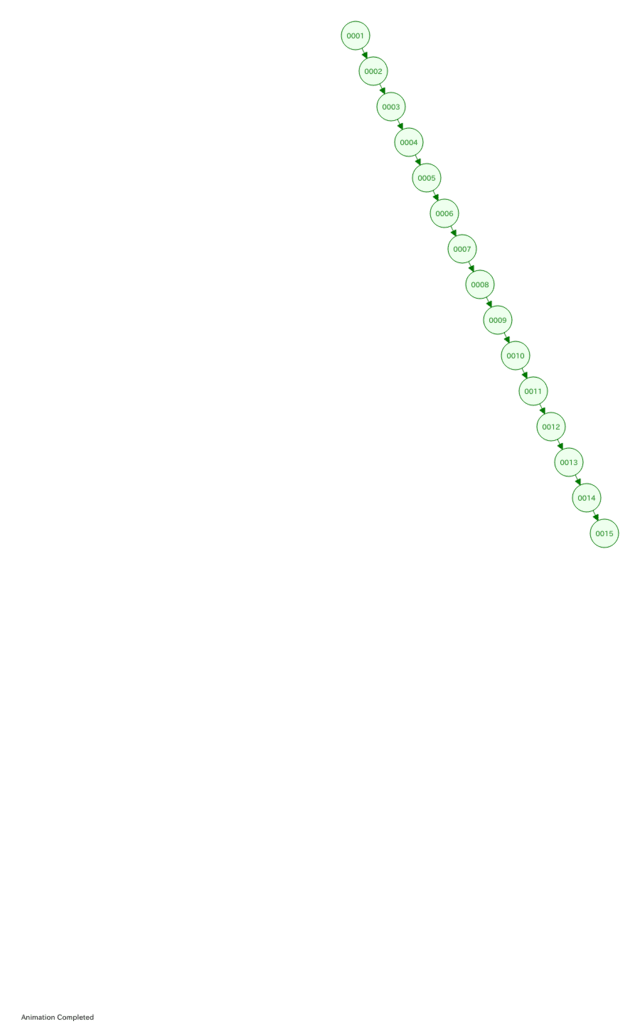
「え?これって二分探索木なの?」

って思う向きもあるかもしんないが、紛れもなく二分探索木だ。

根が1で右の子が2、2の右の子に3、3の右の子に4・・・と数珠つなぎになっている。

しかし、前回の論を見れば分かると思うが、とてもじゃないけど、これは「検索に効率が良い」木とは言えない。

言い換えると、二分探索木は根の選び方がまずは重要だと言う事になる。ここを間違えると検索効率が大幅に落ちるわけだ。

代わって次の木を見てみよう

同じく整数1〜15を用いた二分探索木だが、こっちの方が検索効率が良くなる。どんな節のデータを参照しようと検索の為の再帰回数は4回以下に抑えられるだろう。何故なら木の高さが4だからだ。

このように「どうやって根を選ぶか」「節をどうやって配置していくか」と言うのが二分探索木作成の際の大きなポイントとなる。ここをミスれば検索効率が大幅に落ちる、ってのが二分探索木なんだ。

後者の木を平衡木、と呼ぶ(※2)。

平衡木とは

「すべての葉について、高さ(深さ)がほぼ等しい木 」

の事で、二分探索木を作る際にも平衡木として作らんとアカン、使いモンにならん、って事だ。

ところで後者の平衡木を良く見てみよう。根は8となっていて左の子は「全部8より小さい数の集合」となっている。例外はない。

同様に、根の右の子は「全部8より大きい数の集合」となっている。これも例外はない。

適当に節を選んでみよう。例えば4。4の左の子も全部4より小さい数の集合だ。4の右の子も全部4より大きい数の集合だ。それどころか、4の右にある数も全部4より大きな数の集合だ。

これはどんな節に対しても成り立ってる。例えば10を見ると、10の左の子を含み、10の左側に配置されてる数値は全部10より小さい。同様に10の右側を見ても、右の子を含み全部10より大きい。

繰り返すが、二分探索木はその構造自体が再帰構造なんだ。よってどこを切っても金太郎飴、の如く同じ性質を持っている。

いや、待てよ、と。こんなの上手く行くんか?と思うかもしんない。でも上手く行くんだわ。

一見「節の置き方」には規則性が無いように見えるだろうが、違う。実は規則性があるんだ。

それは、例えば1〜15の整数のリストを与えられた際、それらの数の平均値をまず根とする。8だな。

次に根の左側に来る数値の候補は8より小さな数の集合だ。根の右側に来る数値の候補は8より大きな数の集合になる。

それらから子としての節の候補を選ぶわけだが、ここまで来れば簡単だろう。左側の節には1〜7の平均値が(整数にならなかったら四捨五入でもして)来る。右側の節には9〜15の平均値が来る。

以下、同文、だ。

つまり、うまい具合に与えられたデータの「平均値」を使っていくことによってリストから平衡木が生成出来る、ってこった。

ところで今「平均値」と書いたが、じゃあどんなキーでも「平均値」が定義出来るんだろうか。

例えば今までの例だと1〜15の抜けのない整数のリストを対象にして考えてきたが、じゃあ、「ヌケ」があった時は上手く行くのか。

100歩譲って整数がキーだった場合は上手く行くとしても、じゃあ、キーが文字列だったらどうするんだ。文字aと文字zの平均値なんてどうやって定義するんだ。ましてや文字列"A"と" Zyzzyva"(※3)の「平均値」なんてどうするんだ、と。

ここでちと考え方を変えてみる。

あるリスト(要素が数値なのか文字なのかはたまた文字列なのかは問わない)が与えられた、とする。そのリストを取り敢えず「昇順」にソートする。

そしてそのソートされたリストを二分割した際に来る「真ん中付近」の要素を暫定的に「平均」とするんだ(※4)。

余談だが、この場合の「平均値」のように、何らかの計算をする際のキーポイントと言うか、マーカーのような役割をする値をプログラミング用語でピボットと呼ぶ。

結果、この場合、つまり、平衡木を生成する際のピボットは、Racketだと

(car (drop lst (quotient (length lst) 2)))

で定義出来る、と言う事だ。

ところで、上のように、まずはピボットを選び、ピボットより小さい数値の集合とピボットより大きな数値の集合を考えて再帰・・・と言う論法を見た時、なんか既視感を覚えないだろうか?

そう、実はこのロジック、クイックソートのロジックと全く同じなんだ。

ここで、もう一度、クイックソートのロジックを見てみよう。

(define (qsort lst fn)
　(if (null? lst)
　　'()
　　(let ((pivot (car lst)) (tail (cdr lst)))
　　　`(,@(qsort (filter (lambda (x)
　　　　　　　　　　　(fn x pivot)) tail) fn)
　　　,pivot
　　　,@(qsort (filter (lambda (x)
　　　　　　　　　　((compose not fn) x pivot)) tail) fn)))))

このクイックソートの場合、

ソートアルゴリズムそのもの、なんで与えられたリストを別のソートアルゴリズムでソートする必要はない。
ピボットとしてリストの先頭を使ってる。
返り値として単一のリストを返す前提である。

なんだけど、平衡木を作る場合、

与えられたリストが整列してるとは限らないので、ピボットを計算する為にリストをソートしないといけない。
ピボットとしてはリストをlstとして、(car (drop lst (quotient (length lst) 2)))を利用する。
返り値として単一のリストを返す前提だが、クイックソートはそれをappendで作り出してたが、平衡木の場合、2つの計算結果をそれぞれ左の子と右の子へと詰め込んだリストとなる。

の辺りが違う。

いずれにせよ、大まかなロジックは同じなんで、クイックソートを多少改造するだけで、与えられたリストを平衡木に変換する関数が書けるわけだ。

(define (list->tree lst)
　(if (null? lst)
　　lst
　　(let ((lst (sort lst <)))
　　　(let ((pivot (car (drop lst (quotient (length lst) 2)))))
　　　　`(,pivot ,(list->tree (filter (lambda (x)
　　　　　　　　　　　　　　　(< x pivot)) lst))
　　　　　　　　,(list->tree (filter (lambda (x)
　　　　　　　　　　　　　　　　(> x pivot)) lst)))))))

実際、ランダムな並びの整数列リスト(しかもヌケがある)を与えてもこの関数は平衡木を返してくれる。

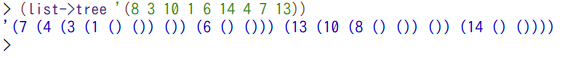
これは次の平衡木を表している。

なお、これは前回の論と同様、「キーのみでの平衡木」になってる。と言う事は実用的な検索システムとしてはまだまだ、だ。

で、今までの流れで見れば分かると思うが、実際一個一個チマチマとデータを「追加」するより、連想リストを二分探索木に一気に変換した方が面白い(笑)。

ここで、前回で見たような連想リストをデータとして用意する。

(define *data*
　'((8 . )
　(3 . )
　(10 . )
　(1 . )
　(6 . )
　(14 . )
　(4 . )
　(7 . )
　(13 . )))

これに対して、連想リストを平衡木に変換する関数を次のようにして定義してみる。ロジックは上で書いたクイックソートの改造版と基本的には全く同じだ。

(define (alist->tree lst)
　(if (null? lst)
　　'()
　　(let ((lst (sort lst < #:key car)))
　　　(match-let (((cons key val) (car (drop lst (quotient (length lst) 2)))))
　　　　`(,key ,val
　　　　　　　,(alist->tree (filter (lambda (x)
　　　　　　　　　　　　　　　　(< (car x) key))
　　　　　　　　　　　　　　　lst))
　　　　　　　,(alist->tree (filter (lambda (x)
　　　　　　　　　　　　　　　　(> (car x) key))
　　　　　　　　　　　　　　　lst)))))))

*data*を与えて実行してみると次のようなリストが返ってくるだろう。

> (alist->tree *data*)
(list ;;; ここから返り値
　7
　
　(list 4 (list 3 (list 1 '() '()) '()) (list 6 '() '()))
(list 13 (list 10 (list 8 '() '()) '()) (list 14 '() '())))
>

これは次のような二分探索木を表している。

これで、やっと手作業で二分探索木をリストで作る苦行から解放されたわけだ(笑)。万歳!

あとは前回見た通り、検索関数をテキトーに作っておけばリストで作った平衡木から自在にデータを引き出せる。

このモデルだと例えばこんなカンジだ(※5)。

(define (tree-search v tree)
　(match-let ((`(,key ,val ,left ,right) tree))
　　(cond ((= v key) val)
　　　　　((< v key) (unless (null? left)
　　　　　　　　　　　(tree-search v left)))
　　　　　(else (unless (null? right)
　　　　　　　　　(tree-search v right))))))

と、二分探索木とその検索関数の役割は十二分に果たしている。

次は文字列をキーとする場合を考えてみよう。

例によって、データを次のようなモノと仮定する。

(define *av-list*
　'(("楪カレン" . )
　("つぼみ" . )
　("森沢かな" . )
　("河北彩花" . )
　("日向かえで" . )
　("東條なつ" . )
　("小花のん" . )
　("今宵こなん" . )
　("八蜜凛" . )))

実はこの連想リスト、写真の並びは前の*data*と全く同じだ。

そして新しいalist->tree関数を定義する。

(define (alist->tree lst)
　(if (null? lst)
　　'()
　　(let ((lst (sort lst string<? #:key car)))
　　　(match-let (((cons key val) (car (drop lst (quotient (length lst) 2)))))
　　　　`(,key ,val
　　　　　　　,(alist->tree (filter (lambda (x)
　　　　　　　　　　　　　　　　(string<? (car x) key))
　　　　　　　　　　　　　　　lst))
　　　　　　　,(alist->tree (filter (lambda (x)
　　　　　　　　　　　　　　　　(string>? (car x) key))
　　　　　　　　　　　　　　　lst)))))))

単に比較関数を文字列用に取っ替えただけ、だ。

そして、*av-list*を新しいalist->tree関数に通すと次のようになる。

> (define *tree* (alist->tree *av-list*))
> *tree*
(list
　"日向かえで"
　
　(list
　　"八蜜凛"
　　
　(list "今宵こなん" (list "つぼみ" '() '()) '())
　(list "小花のん" '() '()))
　(list
　　"楪カレン"
　　
　(list "森沢かな" (list "東條なつ" '() '()) '())
　(list "河北彩花" '() '())))
>

気づいたろうか?

今回も平衡木ではあるが、データの配置が上の平衡木とは全く違う。

このように「文字列比較」で平衡木を形成すると、数値で形成した二分探索木とはデータ配置が全く変わる、と言う事だ。

当然と言えば当然だが、このように実際「計算結果を直接覗けば」色々と腑に落ちる事があるんじゃないか。

このケースのような文字列がキーとなった検索関数は以下のようになるだろう。

(define (tree-search v tree)
　(match-let ((`(,key ,val ,left ,right) tree))
　　(cond ((string=? v key) val)
　　　　　((string<? v key) (unless (null? left)
　　　　　　　　　　tree-search v left)))
　　(else (unless (null? right)
　　　　　　(tree-search v right))))))

単に比較関数と同値判定を文字列用に取っ替えただけ、だが。

いずれにせよ、キチンと検索に性交成功して値を返してくれる。

残る問題は、二分探索木のキーによってわざわざ関数を別々に用意してる、って辺りだ。

これを統合してみるのが最後の作業だ。

(define (list->bst lst (cmp <) #:key (fn identity))
　(define (loop lst cmp fn)
　　(if (null? lst)
　　　'()
　　　(let ((pivot (car (drop lst (quotient (length lst) 2)))))
　　　　(let ((left (loop (filter (lambda (x)
　　　　　　　　　　　　　　(cmp (fn x) (fn pivot)))
　　　　　　　　　　　　　lst) cmp fn))
　　　　　　(right (loop (filter (lambda (x)
　　　　　　　　　　　　　　　(cmp (fn pivot) (fn x)))
　　　　　　　　　　　　　　lst) cmp fn)))
　　　　(cond ((list? pivot) `(,@pivot ,left ,right))
　　　　　　　((pair? pivot) (match-let (((cons k v) pivot))
　　　　　　　　　　　　　　`(,k ,v ,left ,right)))
　　　　　　　(else `(,pivot ,left ,right)))))))
　(loop (sort lst cmp #:key fn) cmp fn))

オプショナル引数とキーワード引数を上手く使ってデフォルトの比較関数を設定する。

あとは使用時に、変換したいリストのキーのデータ型を見て、オプショナル引数とキーワード引数に適当な関数を与えれば良い。要するにこれは高階関数になっている。

検索関数の一般化は、例えば次のようになるだろう。

(define (bst-search v tree (cmp equal?) #:keyfn (kfn <) #:key (fn car))
　(match tree
　　('() #f)
　　(`(,lvp ... ,left ,right)
　　　(cond ((cmp v (fn lvp)) lvp)
　　　　　　((kfn v (fn lvp)) (bst-search v left cmp #:keyfn kfn #:key fn))
　　　　　　(else (bst-search v right cmp #:keyfn kfn #:key fn))))))

返り値は連想リストの如く、元々のデータを丸ごと返すようにしてる。

というのも、連想リストの要素の「キー以外の要素」は単一であるとは限らず、キーも含めて「再利用する可能性」が高いから、だ。

結果、加工が必要なら、戻り値をcarしたりcadrしたりした方が最終的には都合がいいだろう、と言う判断だ。