どうも、囲碁アートの関です!
来月はついに
(囲碁アートマニアはまだ発表待ちですが)
もし出させていただいた場合。
今回は海外のマニアさんもいらっしゃるとのことで、全世界に向けて自分の活動を発表していきたいですね!
でも・・・わし英語しゃべれないし・・・
そもそもしゃべること自体苦手だし・・・
囲碁しかできないんです・・・
あーあ、囲碁だけで、全部できないかなーーー
°˖✧˖°°˖✧▿✧˖°˖✧˖°˖✧˖°°˖✧▿✧˖°˖✧˖°˖✧˖°°˖✧▿✧˖°˖✧˖°˖✧˖°°˖✧▿✧˖°˖✧˖°˖✧˖°°˖✧▿✧˖°˖✧˖°˖✧˖°°˖✧▿✧˖°˖✧˖
というわけで考えました。
囲碁の仕組みだけで言葉を表現する方法を。

そう、モールス信号です。
「-」(ツー)と「・」(トン)の二種類。
たとえば一番有名な「SOS」は
「・・・---・・・」となります。
この二つの要素だけで、いろいろな文字を表すことができます。
おや、二種類といえば・・・
囲碁です。
ーは黒、・は白
っていうことにすれば、モールス信号を表せる
つまり、囲碁だけで会話できる時代が到来するはずだ
ということになるんですね~~~

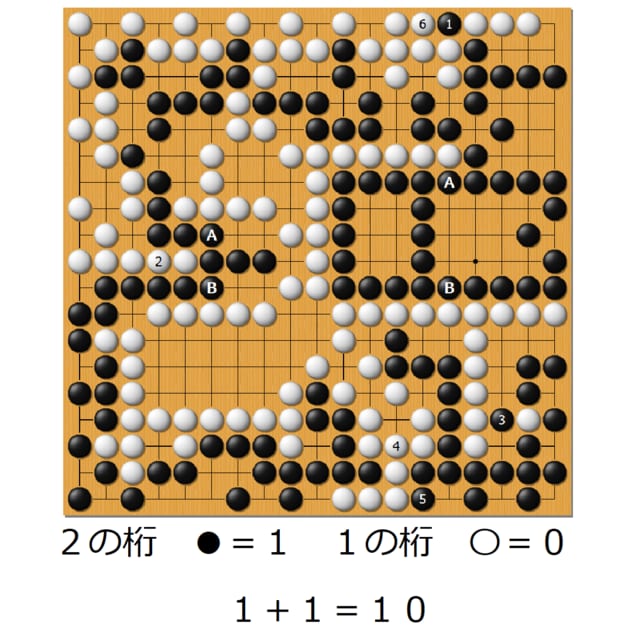
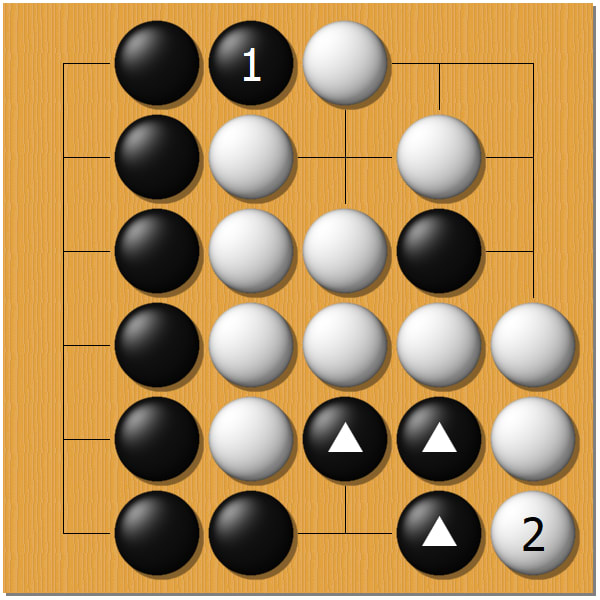
さっそく例題です。
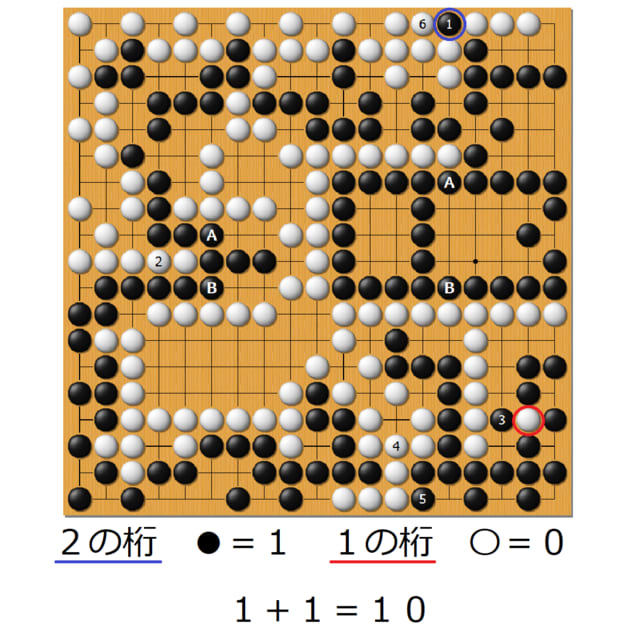
この状況から、囲碁の勝負をしていきます。黒からです。
お互いに、ピンチになっている石があります。
黒は◎の二つで、白は▲のやつです。
ということは黒がチャンス!

ここに打てば(黒1)、白石を囲んで取っちゃうことができます。
白をやっつけたので、上の◎の黒も助かりました。
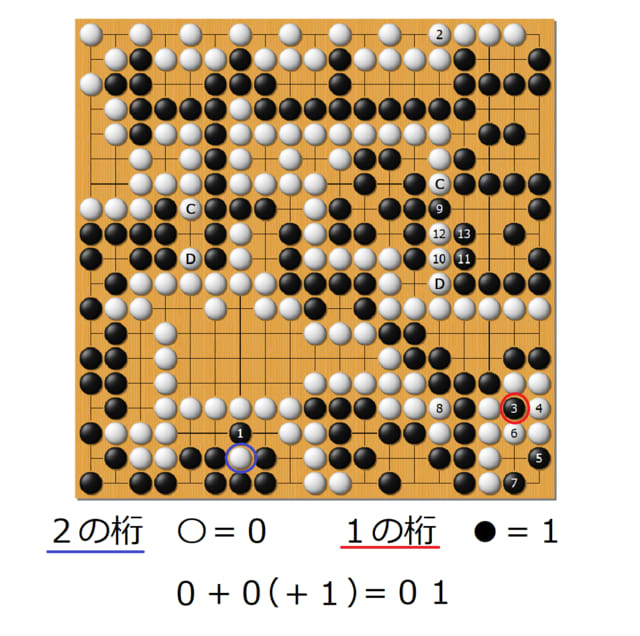
では、次は白はどこにしましょう。

こちらです。下の黒石を白2で取ることができます。

このあとは黒3、白4、黒5と順番に進んで、終わり。(もう陣地が増えず、減らず)
お互い陣地は27目あり、引き分けになりました
・・・
・・・ん?
どこがモールス信号だったん?
勝負を振り返ってみましょう。

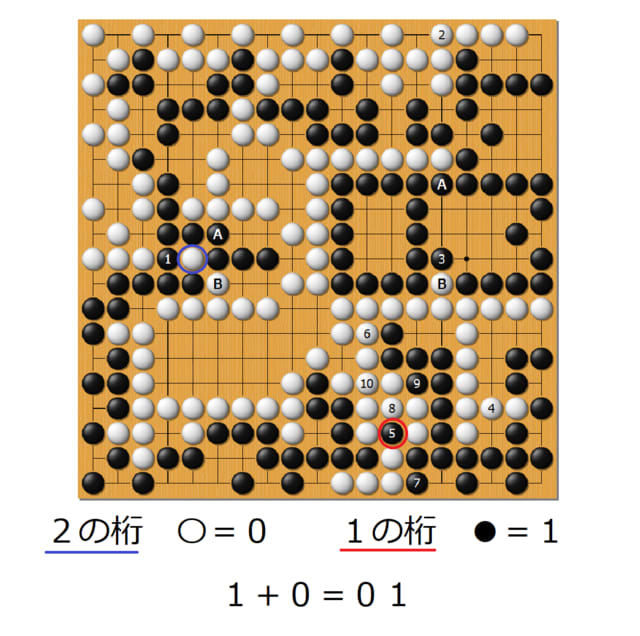
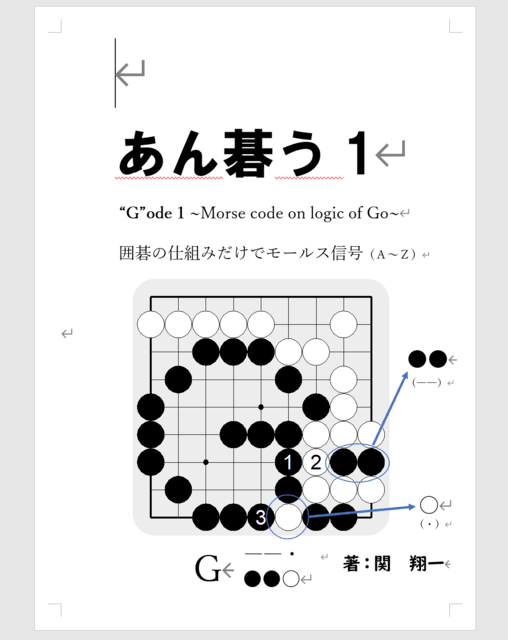
黒の1手目、白の2手目が石を取っていましたが
白石〇→黒石●、という順番で石取りが起こりました。
これをモールス信号に置き換えると
・- というメッセージとなります。
上の表から探してみると、・-は「A」
つまり、この勝負には「A」が込められていたのです・・・!
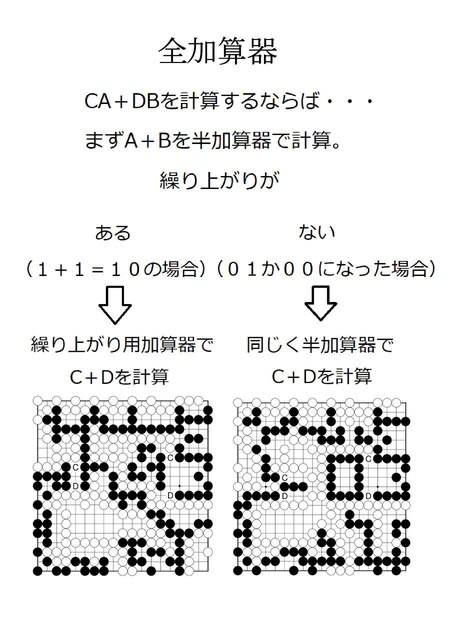
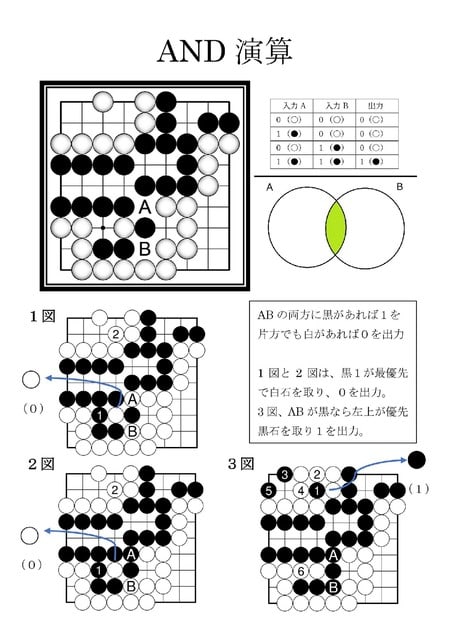
(実は「囲碁計算機」と同じ原理です。取った石の色によって表現しています。
0と1、・とーの違いです)
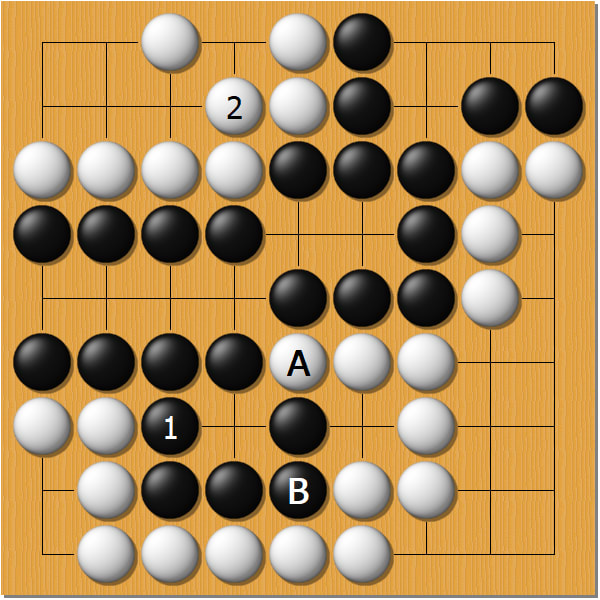
では、こちらはどうでしょう

さっきよりも複雑な形で、囲碁を知っている人でも少し考え込みそう。
これも囲碁の勝負になっており、黒から始めます。
一番いい手を、お互いに打っていきましょう。一手目は・・・?

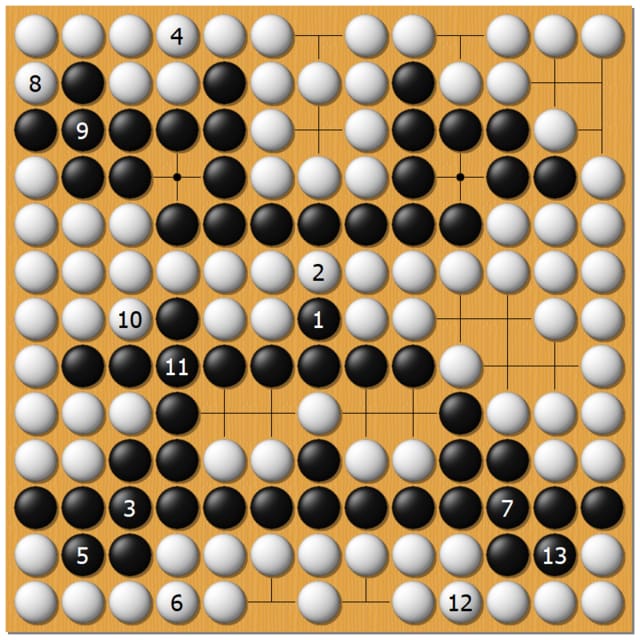
右下黒1で、白3つを取ります。
「・・・」 が出ました。
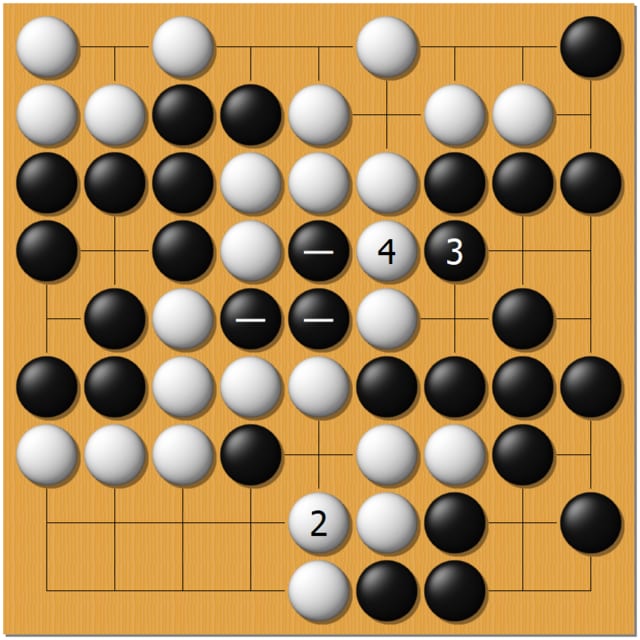
続いて中央で、白4。黒の3つが囲まれました。
「ーーー」ですね。

最後に左上の白3つが取られます。
また「・・・」が出ました。
白10で終わり。(もちろん引き分けになります)
「・・・」→「---」→「・・・」
つまり
「S」→「O」→「S」
が込められていたのでした!!
ピンチになったらこの碁盤を見せれば、誰かが助けてくれます。
いかがでしょう。囲碁はここまでたどり着きました。
何気ない、普通の囲碁のようでも、これからは様々な暗号が込められているかも知れないのです・・・!
まさに「あん碁う」!!
冊子にすべく、製作中です
お楽しみに!