
「QED: The Strange Theory of Light and Matter (2006): Richard P. Feynman」
(Kindle版)(2014)(1986)
内容紹介:
Celebrated for his brilliantly quirky insights into the physical world, Nobel laureate Richard Feynman also possessed an extraordinary talent for explaining difficult concepts to the general public. Here Feynman provides a classic and definitive introduction to QED (namely, quantum electrodynamics), that part of quantum field theory describing the interactions of light with charged particles. Using everyday language, spatial concepts, visualizations, and his renowned "Feynman diagrams" instead of advanced mathematics, Feynman clearly and humorously communicates both the substance and spirit of QED to the layperson. A. Zee's introduction places Feynman's book and his seminal contribution to QED in historical context and further highlights Feynman's uniquely appealing and illuminating style.
2006年刊行、158ページ。初版は1986年刊行
著者について:
Richard P. Feynman (1918-1988): Wikipedia ウィキペディア
Professor of Physics at the California Institute of Technology, known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics for which he proposed the parton model. For contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
理数系書籍のレビュー記事は本書で424冊目。
このタイミングで本書を読んだのは、僕の虫歯がきっかけだった。これはファインマン先生の著作の中でも人気が高い「光と物質のふしぎな理論―私の量子電磁力学 (文庫、2007): R.P.ファインマン」の原書英語版である。
8月上旬から左下の奥歯が痛み出していたのだが、お盆休みでかかりつけの歯科医院がお休みだったので鎮痛剤でしのいでいた。お盆が明けてようやく歯科に通い出した。子供の頃からお世話になっているその医院の先生は科学好きで、科学雑誌Newtonや科学教養書をときどき読んでいる。前回の通院時には読み終えていた「素数に憑かれた人たち ~リーマン予想への挑戦~:ジョン・ダービーシャー」を先生にプレゼントしていた。
いま先生は「『超ひも理論と宇宙のすべてを支配する数式』 (ニュートン別冊)」(詳細)をお読みになっている。治療の合間にこの本をもっていらっしゃり、式のいちばん左の「S」って何?と質問された。これは「作用」というもので日常用語でいう作用とは違い、物理学固有の意味ですよと説明した。残念ながらこの本には説明が書かれていないから、わからないのは無理もない。正しく説明するためには「解析力学」を学ばないといけないし、数式を使わないで解析力学を学ぶのは無理だ。
「作用」を理解してもらうために良い本はないかと考えて思いついたのが「光と物質のふしぎな理論―私の量子電磁力学 (文庫、2007): R.P.ファインマン」(紹介記事)だった。読み終えていた本を2回目の治療のときに持っていって、先生に差し上げた。数式を使わない科学教養書だが少々難しめの本だ。この本の中に「作用」に至る考え方が解説されている。
僕が読んで紹介記事を書いたのは9年前。大好きな本だからもう一度読んでみようと思ったわけだ。ちょうど今は、日本の英語教育の問題に関心が高まり本も2冊読んでいる。英語は繰り返しで学ぶのが良いし、とにかく文章をたくさん読むのが大事だ。ということで英語で読むことにしたわけである。
9年前に書いた日本語版の紹介記事と重複するが、本書の概要をもう少し詳しく説明しておこう。
本書は、ファインマン先生が研究を続けてきた「量子電磁力学(QED: Quantum Electrodynamics)がテーマだ。主な研究対象は光子と電子、そしてその相互作用である。先生が1965年に受賞したノーベル物理学賞も電子についての「繰り込み理論」であり、ファインマン先生が考案した「経路積分」そして「ファインマン図による計算」という手法を含めて量子電磁力学に含まれる。
図を拡大
電子は物質を構成するすべての原子に含まれている基本的な素粒子だ。本書のタイトルが「光子と電子の~」ではなく「光と物質の~」であるのはそのためである。
重力を除けば、この世界の物質現象の99パーセントは量子電磁力学がその基礎となっている。残りの1パーセントは原子核の中でおきている原子核物理学、量子色力学と呼ばれる研究領域で、これらも含めて量子電磁力学は素粒子の標準模型という理論の一部である。(標準模型を知るための科学教養書は「強い力と弱い力:大栗博司」がお勧め。)
ファインマン先生が科学者になるまでにわかっていたこと
19世紀末までに古典電磁気学はマックスウェルの方程式として完成し、光が波動であることが確認されていた。また、トムソンの実験により電子が発見されたのも19世紀末のことである。電流は多数の電子の流れであることも受け入れられていた。
20世紀に入り、1905年に光が粒子性をもつ「光量子」であることがアインシュタインにより発見される。また電子のほうもド・ブロイによって波動としての振る舞いが提唱され、光も電子も「粒子性」と「波動性」を兼ね備えた「量子」というくくりで考えられることになった。そして1925年に誕生した量子力学は量子の物理的性質を研究する新しい学問領域として急速に進展することになる。その波動力学としての基礎となるのが「シュレーディンガー方程式」だ。また量子の粒子性をあらわすのが「ハイゼンベルクの運動方程式」と呼ばれている基礎方程式である。
この2つの基礎方程式は見かけはまったく違うが、1932年までにフォン・ノイマンによって数学的には同じであることが証明された。その証明は「量子力学の数学的基礎: J.v.ノイマン」という本として出版されている。
1905年は「奇跡の年」と呼ばれている。この年にアインシュタインが発表した特殊相対性理論は、この世界が4次元の「時空」として存在していることを示した。量子力学はもともと3次元空間と1次元の時間を舞台として記述されているため、4次元の時空を舞台とする形に書き直す必要がでてきた。
量子力学と特殊相対性理論を統合するのが「相対論的量子力学」である。これを成し遂げたのがポール・ディラックであり、1928年に「ディラック方程式」として発表した。この方程式から導かれる予言によると「電子はスピンしていて、そのために磁気モーメントをもつ」ということ、そして「プラスの電荷を帯びた電子(陽電子と名付けられた)」があるということである。そしてディラックは磁気モーメントの値をちょうど1だと計算し、陽電子のほうはアンダーソンによる実験で1932年に検出された。陽電子は電子にとっての反粒子である。(参考:「ディラックによる陽電子の予言(1928年)」)
そして粒子と反粒子が真空中で対消滅したり、真空から粒子と反粒子が対消滅する現象も理論的、実験的に示された。
ファインマン先生が科学者としてのスタートを切るまでに、ここまでのことがわかっていた。
本書の内容
ここからが相対論的量子力学の後に続く量子電磁力学の話である。章立てを日本語で書けば、このようになる。
ファインマンの挨拶
1)はじめに
2)光の粒子
3)電子とその相互作用
4)未解決の部分
1)はじめに
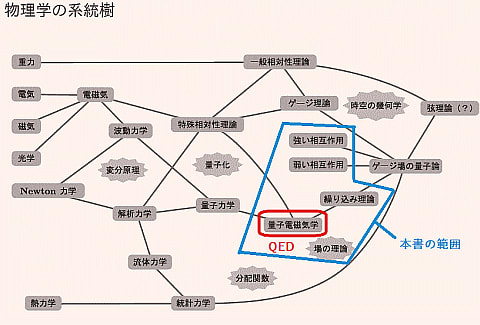
量子電磁力学のあらましについての解説の後、ファインマン先生は光(光子)がガラスに部分反射する現象を取り上げる。図の左側のように、左上の光源からガラスに向けて光を照射すると、4パーセントが反射して検出器Aに達し、残りの96パーセントはガラスを通過して検出器Bに達する。
ガラスにとって光は一様のはずだ。反射させる光と通過させる光を、どのようにしてより分けているのだろうか?ここで、先生はひとつの「矢印」を提案する。量子電磁力学で強力な道具となる光の波長に比例して超高速回転するストップウォッチの針のような矢印だ。青い単色光の矢印は赤い単色光の2倍速く回転する。光子の進みにあわせてこの矢印は一定速度で回転するのだと考える。
矢印の長さはその物理事象がおきる確率に結びついている。すなわち右の図で矢印の長さを0.2としているのは、その2乗が反射する確率0.04(4パーセント)であることを意味している。そしての矢印のことを「確率振幅(probability amplitude)」または省略して「振幅(amplitude)」と呼ぶことにした。つまり確率振幅は長さと方向をもつ「回転するベクトル」なのである。
ところで、光はガラスの表面だけでなくガラスの中を通過し、光源から見て裏面でも反射するはずだ。もし裏面でも4パーセント反射すると、表面の4パーセントの反射と合わせて合計8パーセント反射するはずだから、おかしなことになる。では表面と裏面でそれぞれ2パーセントずつ反射しているのだろうか?合わせて4パーセントになるからつじつまが合う。
そこで、実際にどうなるか実験をしてみた。ところが不思議なことがおきたのだ。ガラスの厚さを少しずつ変えながら赤と青の単色光で部分反射の実験をしてみると、次のような結果が得られた。横軸がガラスの厚さ、縦軸が反射率である。
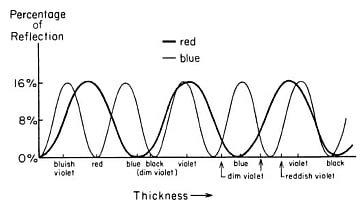
ガラスの厚さが増えるにしたがい、反射率は0パーセントから16パーセントまでの間を周期的に変化する。赤色と青色ではその周期が2倍異なっている。いったい何がおきているのだろうか?この章では「矢印の計算」を紹介しながら、この不思議な現象のからくりを解き明かしている。ガラスによる光の反射と透過という日常みられる現象が、私たちが理解しているのとはまったく違うものであることがこの章で明らかにされるのだ。
2)光の粒子
この章では鏡による光の反射(光子の反射)が取り上げられる。Sから放出された光子は鏡の中央で反射してPに達する。このとき鏡の中央では入射角と反射角は等しくなる。だから光子の飛ぶ経路は、この図のようになるはずだ。
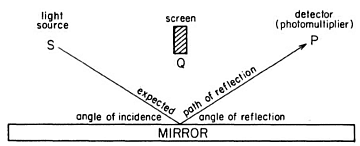
「入射角と反射角は等しい」ことは中学の理科で習うし、高校では幾何光学として習う。「ホイヘンスの原理」や「スネルの法則」のことである。
けれども、ここに重大な謎が潜んでいる。光子の経路がどのようにして決まったのかということだ。Sを出発した光子は鏡の中央を目指して飛んで行ったのだろうか?Sを出発したときに光子は鏡の中央を目指して飛びなさいと命令されていたのだろうか?または反射地点を知っていたのだろうか?中学と高校の理科では学んでいないはずである。
「ホイヘンスの原理」を一般化すると「フェルマーの原理(最小作用の原理)」が得られる。これは光は「目的地に最小時間で着くような経路を選ぶ」という原理だ。これで解決するだろうか?最小時間になるような経路を見つけるためには、目的地が決まっていなければならない。光子がSを出発したときに経由地(鏡の中央)や目的地Pを知っていたはずがない。
ファインマン先生も高校生のとき、この問題にとても興味を持っていた。そして先生がたどり着いたのが「光子は目的地に到達するために可能なあらゆる経路をとる」という結論だった。それはこのような図であらわされる。
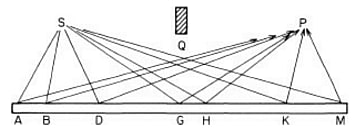
この考えによればSから飛び出し、Aで反射してPに達する経路(SAP)や、同様にSBP、SCP、SDP、...、SMPの経路も「可能性として」考えられる。これらの経路を光子は「すべて」通っているのだと先生は考えた。たった1つの光子についてのことである。
そしてファインマン先生は、この現象を「矢印の足し算」として次のようにあらわした。
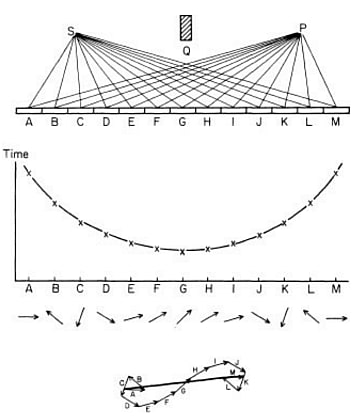
反射点が変わるとSからPまでの経路の長さ、すなわち光子がPに到達するまでの所要時間が変わる。SからPに到達するまでの所要時間を真ん中のグラフの縦軸にとると、図のようにU字型のグラフとなる。Pに向かって光子が進む間に「光の矢印」は回転しているから、Pに着いたときの矢印の向きは、グラフの縦の長さ(所要時間)によって違っている。
それぞれの反射点の下に光子ががPに到達したときの矢印を書く。そして最後にこれらの矢印のすべてを「ベクトルの足し算」として計算するのだ。するとその合計はいちばん下の太くて長い「最終矢印」となる。この最終矢印の長さの2乗が、この事象(光子がSからでて鏡で反射してPに到達する事象)が起きる確率とみなされる。光子は1つであっても鏡のAからMのすべての場所で反射しているのだ。
さて、この最終矢印の方向を決めるにあたって貢献度が高い小さな矢印はどれだろうか?小さい矢印をひとつずつ見てみると、鏡の中央に近い矢印が最終矢印と同じような向きであることがわかる。つまり、鏡の中央で反射するという現象がおきる確率を高めているのは、これら中央の矢印(確率振幅)たちなのである。
では、中央以外の矢印を考えなくてもよいのでは?と思うかもしれない。でもそれは違うのだ。実際に鏡の端に近い部分でも光子の反射がおきていることを、ファインマン先生は次の実験で示している。(この記事には書かないでおく。)ともかく、光子は鏡のあらゆるところで反射しているのだ。そして本書には書かれていないが、このような「可能なすべての経路の矢印を足し合わせる」ことを物理学では「経路積分」と呼んでいる。
この実験で考える「可能なすべての経路」とは、このようにぐにゃぐにゃ曲がった経路も合わせて計算するのだ。
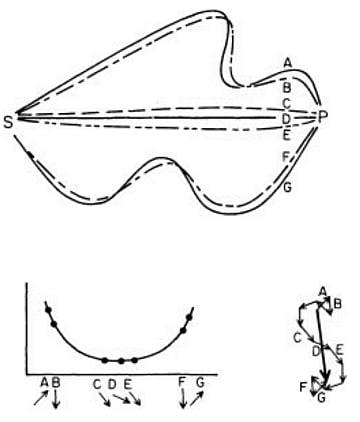
私たちは、このように現象が起きる確率を通してしか自然の姿を見ることができない。これが量子電磁力学、量子力学が私たちに教えてくれることだ。
この章では鏡による反射の例に続いて、水中やガラスの中で光が遅くなるしくみ、水面やガラスの表面で光が屈折するしくみ、平行に入射した光がレンズで屈折して一点に集まるしくみ、光の回折がおきるしくみなどが矢印の計算方法を使って解説される。これらはすべて量子電磁力学によって解明された物理現象である。
3)電子とその相互作用
前の章では光の反射の現象を、経路積分を使ったマクロな視点から解説したが、この章ではこの現象を光子と電子の相互作用という素粒子の視点、ファインマン図を紹介しなから解説する。経路積分の考え方はファインマン図に活かされているのだ。
光子とは若干方法が異なるが、電子も同じように矢印を使って計算することができる。(詳細は本書で解説される。)
実をいうとガラスによる光子の部分反射は、鏡の表面と裏面だけでなく、ガラスの中全体でおきているのだ。このような図になる。矢印の足し算をして確率振幅の合計を求めると、不思議なことに表面と裏面だけで反射するときの結果と一致するのである。
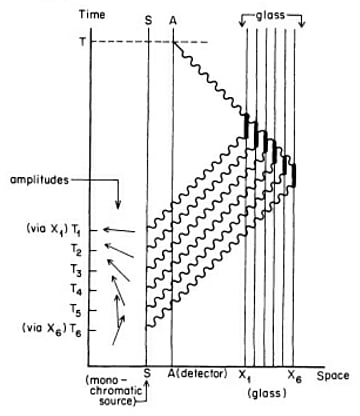
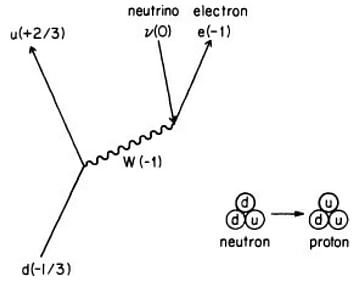
そして、次に紹介されるのは光子が壁に衝突するボールのように反射しているのではないということなのだ。ガラス中の電子が入射してきた光子を吸収し、その後で電子が光子を放出する。つまり入射した光子と反射した光子は違う光子なのである。したがって電子と光子の相互作用を考えるのが反射、屈折、吸収などの光学現象を解き明かすカギとなる。たとえば、ファインマン図を使うと入射した光子が電子に吸収される現象はこの図のようにあらわされる。1と2を結ぶ直線が電子の経路、波線が光子の経路である。
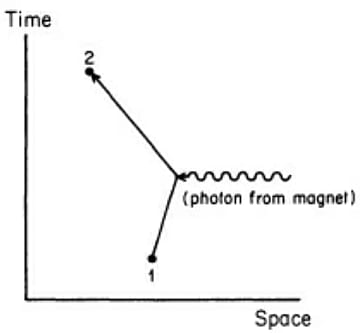
ファインマン図では空間座標を横軸に、時間座標を縦軸にとっている。つまり特殊相対論の4次元時空内にあらわした素粒子の相互作用の図なのだ。ファインマン図では線と点の結びつき方が同じものを同一視する。マクロな世界の光子の経路のように曲線を描いたりすることは考慮しない。
4次元時空内で可能な経路というものを考えてみよう。これは時刻0にS(Start)の位置にある電子が、時刻7にG(Goal)の位置に達するという状況だ。可能な経路は無数あるのだが、ここには赤、青、緑の3つの経路だけ描いておいた。
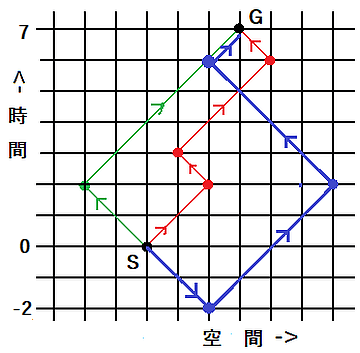
ここで青の経路に注目してほしい。Sから右下に伸びている矢印は、空間座標は増えているものの、時刻は0からマイナス2に減っている。電子が時間を逆行しているのだ。特殊相対論を満たしている経路積分では時間をさかのぼる経路も「可能な経路」のうちに含めて考える。
けれども、物理法則は時間をさかのぼるタイムトラベルを禁じている。物事の因果関係が崩壊してしまうからだ。物事の原因は結果よりも必ず先に起きなければならない。因果関係が逆転すると入学試験を受ける前に合格通知が届くようなことになってしまう。
ファインマン図、量子電磁力学ではこの矛盾を、反粒子を使って解決している。理論上「時間を逆行する電子」は「時間を順行する陽電子」に同一視されるからだ。電子の反粒子は陽電子、そして光子の反粒子は光子である。
左側の図は、未来からやってきた光子が過去から来た電子とぶつかり、電子が向きを変えて未来から過去へとさかのぼっていく様子ともとらえることができる。同様に右側の図は光子から、未来へ飛んでいく電子と過去へ飛んでい電子が対生成される様子である。
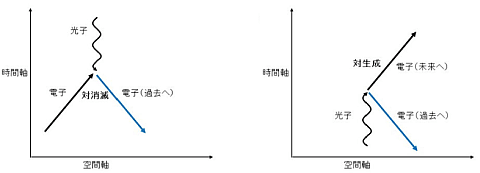
この考え方に従えば、未来からやってきた光子を「未来へ飛んでいく光子」、過去へさかのぼる電子を「未来へ飛んでいく陽電子」と考え、つじつまが合って因果関係が保たれる。
次にファインマン図を使った量子電磁力学の最大の成果、つまり電子の磁気モーメントの値を極めて正確に計算できたことが解説される。理論値と実験値がとてつもなく高い精度で一致したことが、量子電磁力学の正しさを裏付けることになった。
再掲するが、ディラックが電子の磁気モーメントを1だと計算したときのファインマン図はこのようなものである。

この4次元時空で可能なあらゆる経路というのは、ファインマン図で電子のスタート地点とゴール地点が一致しているという条件だけでなく、電子の放出や吸収など可能なあらゆる事象も考慮されることになるのだ。つまり、上の図を1次の相互作用の図とすれば、2次、3次、3次...と段階的に複雑な事象を描いたファインマン図を使って近似の計算精度を上げていく。たとえば上と同じ事象であっても、次のような図であらわされることになる。
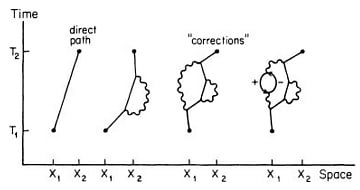
電子の場合、この段階的な近似計算は、驚くほど速く数値が収束していく。計算方法は本書で詳しく解説している。このような計算を経て電子の磁気モーメントの値が高い精度で求められていったのだ。その結果、磁気モーメントの値は1ではなく、理論値は1.00115965246、実験値は1.00115965221となった。末尾の桁には±4くらいの誤差がある。
確率振幅を意味する「矢印」は光子や電子ひとつひとつに紐づいているのではないことを強調しておこう。粒子が複数あれば、複数の粒子の状態に対して1本の矢印が紐づいている。複数の初期状態から最終状態に至る矢印の長さの2乗がその物理現象が起きる確率であると考えるのだ。
確率振幅(矢印)は向きと長さをもったベクトルである。それは複素平面上にある矢印とみなすことができる。つまり確率振幅は複素数の値をとる。電子についてのシュレディンガー方程式に含まれる波動関数も複素数の値をとり、これは確率振幅とみなされている。波動関数の2乗が電子の存在確率であるというのが「ボルンの確率解釈」だ。つまりこれまでの説明で、矢印の長さを2乗するということは、その物理現象がこの世界に実体化する確率を求めていたのである。
また、矢印の計算は可能な経路を計算するときは足し算、時間の経過に従った2つの事象を計算するときは掛け算になるということを補足しておこう。
電子はすべての物質に含まれている粒子である。電子と光子の相互作用を解き明かす量子電磁力学は、この世界のほとんどの物質現象の基礎とみなされている。原子や分子の化学結合、化学反応、絶縁体と導電体、物質が透明か不透明か、空が青い理由、なぜテーブルや机が硬いのか、物にさまざまな色があること、燃やすとなぜ炎がでるのかなどは、すべて量子電磁力学がもとになって生じている。
矢印の計算は「光子の作用」、「電子の作用」、「光子と電子の相互作用」の3種類しかない。自然が私たちに見せる多様性のほとんどが、量子電磁力学の3種類の原理がもとになっているのである。
4)未解決の部分
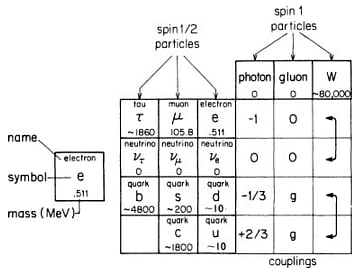
第4章では電子と光子の後に発見された素粒子について解説する。原子核を構成する陽子や中性子は、根源的な素粒子ではなくクォークから構成されていることがわかった。量子電磁力学の矢印の計算による手法は、原子核の中の粒子についても10パーセントという精度で成り立つことが示された。しかし、その誤差は原子核内の物理学が電子や光子の物理学と本質的に違うことを意味している。
ただしファインマン図や経路積分は原子核内の素粒子に対しても有用なツールであり、たとえばクォークを含んだ相互作用では次のような図を使って計算が行われている。経路積分の手法は「シュレーディンガー方程式」や「ハイゼンベルクの運動方程式」と数学的に同等であることがダイソンによって証明された。これは経路積分やファインマン図の手法の有効性を裏付けるものだ。そして量子力学は原子核の中でも成り立っているのである。
ファインマン図については、この動画で理解するとよいだろう。
【3分解説】ファインマン図
そしてこの章では素粒子物理学の発展史が順に解説される。この本が出版された1986年であるから、1995年に発見されたトップクォーク、そして2012年に発見されたヒッグス粒子は言及されていない。1986年の時点では電弱理論、量子色力学(強い相互作用)までである。あとニュートリノの質量もゼロだとされていた。(実際にはわずかながら質量があることがその後確認された。)繰り込み理論は軽く紹介されていた。
本書の一部だけをかいつまんで紹介させていただいた。ファインマン先生の著書、講義はどれをとってもエキサイティングだ。読む者、聴く者の心をつかみ、理路整然と続ける話の中で先入観や誤解を溶かし、まったく思いがけない世界へ私たちを導いてくれる。このようなスタイルで物理学や数学を語れるような人になりたいと、つくづく思ってしまうのだ。
英語版と日本語版について
科学英語の読解トレーニングにはうってつけの本だと思った。主題は光子と電子、その他の素粒子だけであること、計算の方法も一貫しているから、英文のパターンも限られている。読んでいくうちに慣れてくるからスピードも上がる。
日本語版は薄い文庫本だが、英語で読むと4日かかった。英語だと一字一句精読することになるから書かれていることをすべて吸収できる。僕がどれだけ熱中していたかは「この連投ツイート」をご覧になればおわかりになると思う。
英語版はファインマン先生の姿が載っている2006年版をKindle端末で読んだ。1988年に亡くなったファインマン先生が手にしたのは1986年版である。そしていちばん新しいのが2014年に刊行されている。
「QED: The Strange Theory of Light and Matter (2006): Richard P. Feynman」
(Kindle版)(2014)(1986)



日本語版はこの2冊。1986年の英語版が刊行されてすぐ、ファインマン先生が大貫昌子さんを翻訳者に指名したという。大貫さんは「ご冗談でしょう、ファインマンさん」を訳して先生の信頼を得ていたからだ。先生は1987年に刊行された日本語訳(単行本)を手にしてお喜びになったに違いない。
「光と物質のふしぎな理論―私の量子電磁力学 (文庫、2007): R.P.ファインマン」(紹介記事)
「光と物質のふしぎな理論―私の量子電磁力学 (単行本、1987): R.P.ファインマン」


講義の動画、リスニングのトレーニング
この本の元になった講義は1979年と1983年に行われたようだ。1979年に行われた講義は、こちらからご覧いただける。本を読んでからだと講義がわかりやすい。(動画を検索)
QED: Photons-Corpuscles of Light (Richard Feynman 1/ 4)
第1回 第2回 第3回 第4回 プレイリスト The Vega Science Trustの公開動画
各回の講義の後に行われた質疑応答が素晴らしい。本には書かれていないことについて、興味深い話を先生はたくさんお話しになっている。
1983年に行われた講義もYouTubeでご覧いただける。こちらのほうが画質がよい。本書の内容は第2回から始まる。
Richard Feynman: Quantum Mechanical View of Reality 1
第1回 第2回 第3回 第4回
NHKにはファインマン先生をCGで蘇らせて、この4回にわたる名講義を再現した科学番組を作ってもらいたいと思うのだ。また、ニュートンプレス社には本書の内容を「別冊ニュートン」として刊行してもらいたいとも思った。テーマがテーマだけにビジュアルなイラストで魅力的な紙面が満載の本になると思う。
次の動画は本書の内容に沿っているのでお勧めだ。光のガラスによる部分反射の実験と鏡による反射の実験、ファインマン図を使って光子と電子の相互作用を解説している。英語字幕付きなのでリスニングの練習用に使ってもよいだろう。英語がわからなくても見ているだけで楽しめると思う。
Quantum Electrodynamics
経路積分とファインマン図は、次の動画で学ぶとよい。とても詳しく解説している。
Feynman's Infinite Quantum Paths | Space Time(経路積分の解説動画)
The Secrets of Feynman Diagrams | Space Time(ファインマン図の解説動画)
この2つの動画は「量子力学の再生リスト」の一部である。
ファインマン先生による量子電磁力学の教科書
ファインマン先生は量子電磁力学の教科書をお書きになっている。アマゾンから販売されているほか、著作権切れであるため無料で読むこともできる。
「Quantum Electrodynamics: Richard P. Feynman」(Kindle版)

無料版(1961年刊行):
Quantum Electrodynamics - R.P. Feynman (PDF)
https://archive.org/details/QuantumElectrodynamics/page/n49
フランス語版とドイツ語版
熱が入ってフランス語版を注文してしまった。届いたら通読してみたい。(通読中の連投ツイート)(紹介記事)
「Lumière et matière - Une étrange histoire: Richard P. Feynman」(Amazon.fr)
「QED: Die seltsame Theorie des Lichts und der Materie: Richard P. Feynman」(Kindle版)


フランス語の内容紹介:
" Et maintenant, attachez vos ceintures. Non pas que ce soit particulièrement difficile à comprendre, mais tout simplement parce que ça va vous sembler le comble du ridicule. Jugez-en : nous dessinons des petites flèches sur une feuille de papier ! C'est tout. "
L'électrodynamique quantique, qui décrit les interactions entre lumière et matière, prototype des théories de la physique moderne, devient un jeu d'enfant quand elle est expliquée par un de ses créateurs. Richard Feynman montre que les notions les plus difficiles sont explicables sans formalisme mathématique et que leur sens profond est à la portée de tous.
Un sommet de la vulgarisation scientifique.
ドイツ語の内容紹介:
Der amerikanische Physiker Richard P. Feynman galt als einer der größten theoretischen Physiker dieses Jahrhunderts. Für seine Beiträge zur Theorie der Quantenelektrodynamik erhielt er 1965 (mit zwei Kollegen) den Nobelpreis für Physik. Mit dieser Quantenelektrodynamik – kurz QED – befasst sich dieses Buch, in dem er erklärt: "Mein Hauptanliegen ist, die seltsame Theorie des Lichts und der Materie, oder richtiger die Wechselwirkung zwischen Licht und Elektronen, so genau wie möglich zu beschreiben." Der Leser wird Feynmans lebendige und unterhaltsame Art der Darstellung genießen, wenn ihm der berühmte Physiker und begabte Lehrer eine des maßgeblichen physikalischen Theorien dieses Jahrhunderts erklärt.
関連記事:
光と物質のふしぎな理論―私の量子電磁力学: R.P.ファインマン
https://blog.goo.ne.jp/ktonegaw/e/4b34cd4e7d077d037022e62734d1ee76
Lumière et matière - Une étrange histoire: Richard P. Feynman(光と物質のふしぎな理論)
https://blog.goo.ne.jp/ktonegaw/e/625073adb96b546870720092abd5158d
ファインマンの経路積分に入門しよう!
https://blog.goo.ne.jp/ktonegaw/e/0f47de5854daf4eb38339a73791544a8
ファインマン先生の自伝本と講演本
https://blog.goo.ne.jp/ktonegaw/e/9bf47cf51085c74caf34a11068a17285
ファインマン物理学(英語版)が全巻ネット公開されました。
https://blog.goo.ne.jp/ktonegaw/e/e94dd49d7d8cc395e29d37927e30173d
万有引力の法則(逆2乗則)の逆問題を解説する本と動画(ファインマンによる解法)
https://blog.goo.ne.jp/ktonegaw/e/2cd381bca4546d23968b31cfad4a9be9
開平と開立(第5回): ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb
#Feynman100: ファインマン先生、生誕100周年セレモニー&シンポジウム
https://blog.goo.ne.jp/ktonegaw/e/11dd9238ebcbc37915920a2dab553c82
強い力と弱い力:大栗博司(標準模型について学べる科学教養書)
https://blog.goo.ne.jp/ktonegaw/e/06c3fdc3ed4e0908c75e3d7f20dd7177
メルマガを書いています。(目次一覧)

応援クリックをお願いします。








(Kindle版)(2014)(1986)
内容紹介:
Celebrated for his brilliantly quirky insights into the physical world, Nobel laureate Richard Feynman also possessed an extraordinary talent for explaining difficult concepts to the general public. Here Feynman provides a classic and definitive introduction to QED (namely, quantum electrodynamics), that part of quantum field theory describing the interactions of light with charged particles. Using everyday language, spatial concepts, visualizations, and his renowned "Feynman diagrams" instead of advanced mathematics, Feynman clearly and humorously communicates both the substance and spirit of QED to the layperson. A. Zee's introduction places Feynman's book and his seminal contribution to QED in historical context and further highlights Feynman's uniquely appealing and illuminating style.
2006年刊行、158ページ。初版は1986年刊行
著者について:
Richard P. Feynman (1918-1988): Wikipedia ウィキペディア
Professor of Physics at the California Institute of Technology, known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics for which he proposed the parton model. For contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
理数系書籍のレビュー記事は本書で424冊目。
このタイミングで本書を読んだのは、僕の虫歯がきっかけだった。これはファインマン先生の著作の中でも人気が高い「光と物質のふしぎな理論―私の量子電磁力学 (文庫、2007): R.P.ファインマン」の原書英語版である。
8月上旬から左下の奥歯が痛み出していたのだが、お盆休みでかかりつけの歯科医院がお休みだったので鎮痛剤でしのいでいた。お盆が明けてようやく歯科に通い出した。子供の頃からお世話になっているその医院の先生は科学好きで、科学雑誌Newtonや科学教養書をときどき読んでいる。前回の通院時には読み終えていた「素数に憑かれた人たち ~リーマン予想への挑戦~:ジョン・ダービーシャー」を先生にプレゼントしていた。
いま先生は「『超ひも理論と宇宙のすべてを支配する数式』 (ニュートン別冊)」(詳細)をお読みになっている。治療の合間にこの本をもっていらっしゃり、式のいちばん左の「S」って何?と質問された。これは「作用」というもので日常用語でいう作用とは違い、物理学固有の意味ですよと説明した。残念ながらこの本には説明が書かれていないから、わからないのは無理もない。正しく説明するためには「解析力学」を学ばないといけないし、数式を使わないで解析力学を学ぶのは無理だ。
「作用」を理解してもらうために良い本はないかと考えて思いついたのが「光と物質のふしぎな理論―私の量子電磁力学 (文庫、2007): R.P.ファインマン」(紹介記事)だった。読み終えていた本を2回目の治療のときに持っていって、先生に差し上げた。数式を使わない科学教養書だが少々難しめの本だ。この本の中に「作用」に至る考え方が解説されている。
僕が読んで紹介記事を書いたのは9年前。大好きな本だからもう一度読んでみようと思ったわけだ。ちょうど今は、日本の英語教育の問題に関心が高まり本も2冊読んでいる。英語は繰り返しで学ぶのが良いし、とにかく文章をたくさん読むのが大事だ。ということで英語で読むことにしたわけである。
9年前に書いた日本語版の紹介記事と重複するが、本書の概要をもう少し詳しく説明しておこう。
本書は、ファインマン先生が研究を続けてきた「量子電磁力学(QED: Quantum Electrodynamics)がテーマだ。主な研究対象は光子と電子、そしてその相互作用である。先生が1965年に受賞したノーベル物理学賞も電子についての「繰り込み理論」であり、ファインマン先生が考案した「経路積分」そして「ファインマン図による計算」という手法を含めて量子電磁力学に含まれる。

図を拡大
電子は物質を構成するすべての原子に含まれている基本的な素粒子だ。本書のタイトルが「光子と電子の~」ではなく「光と物質の~」であるのはそのためである。
重力を除けば、この世界の物質現象の99パーセントは量子電磁力学がその基礎となっている。残りの1パーセントは原子核の中でおきている原子核物理学、量子色力学と呼ばれる研究領域で、これらも含めて量子電磁力学は素粒子の標準模型という理論の一部である。(標準模型を知るための科学教養書は「強い力と弱い力:大栗博司」がお勧め。)
ファインマン先生が科学者になるまでにわかっていたこと
19世紀末までに古典電磁気学はマックスウェルの方程式として完成し、光が波動であることが確認されていた。また、トムソンの実験により電子が発見されたのも19世紀末のことである。電流は多数の電子の流れであることも受け入れられていた。
20世紀に入り、1905年に光が粒子性をもつ「光量子」であることがアインシュタインにより発見される。また電子のほうもド・ブロイによって波動としての振る舞いが提唱され、光も電子も「粒子性」と「波動性」を兼ね備えた「量子」というくくりで考えられることになった。そして1925年に誕生した量子力学は量子の物理的性質を研究する新しい学問領域として急速に進展することになる。その波動力学としての基礎となるのが「シュレーディンガー方程式」だ。また量子の粒子性をあらわすのが「ハイゼンベルクの運動方程式」と呼ばれている基礎方程式である。
この2つの基礎方程式は見かけはまったく違うが、1932年までにフォン・ノイマンによって数学的には同じであることが証明された。その証明は「量子力学の数学的基礎: J.v.ノイマン」という本として出版されている。
1905年は「奇跡の年」と呼ばれている。この年にアインシュタインが発表した特殊相対性理論は、この世界が4次元の「時空」として存在していることを示した。量子力学はもともと3次元空間と1次元の時間を舞台として記述されているため、4次元の時空を舞台とする形に書き直す必要がでてきた。
量子力学と特殊相対性理論を統合するのが「相対論的量子力学」である。これを成し遂げたのがポール・ディラックであり、1928年に「ディラック方程式」として発表した。この方程式から導かれる予言によると「電子はスピンしていて、そのために磁気モーメントをもつ」ということ、そして「プラスの電荷を帯びた電子(陽電子と名付けられた)」があるということである。そしてディラックは磁気モーメントの値をちょうど1だと計算し、陽電子のほうはアンダーソンによる実験で1932年に検出された。陽電子は電子にとっての反粒子である。(参考:「ディラックによる陽電子の予言(1928年)」)
そして粒子と反粒子が真空中で対消滅したり、真空から粒子と反粒子が対消滅する現象も理論的、実験的に示された。
ファインマン先生が科学者としてのスタートを切るまでに、ここまでのことがわかっていた。
本書の内容
ここからが相対論的量子力学の後に続く量子電磁力学の話である。章立てを日本語で書けば、このようになる。
ファインマンの挨拶
1)はじめに
2)光の粒子
3)電子とその相互作用
4)未解決の部分
1)はじめに
量子電磁力学のあらましについての解説の後、ファインマン先生は光(光子)がガラスに部分反射する現象を取り上げる。図の左側のように、左上の光源からガラスに向けて光を照射すると、4パーセントが反射して検出器Aに達し、残りの96パーセントはガラスを通過して検出器Bに達する。

ガラスにとって光は一様のはずだ。反射させる光と通過させる光を、どのようにしてより分けているのだろうか?ここで、先生はひとつの「矢印」を提案する。量子電磁力学で強力な道具となる光の波長に比例して超高速回転するストップウォッチの針のような矢印だ。青い単色光の矢印は赤い単色光の2倍速く回転する。光子の進みにあわせてこの矢印は一定速度で回転するのだと考える。
矢印の長さはその物理事象がおきる確率に結びついている。すなわち右の図で矢印の長さを0.2としているのは、その2乗が反射する確率0.04(4パーセント)であることを意味している。そしての矢印のことを「確率振幅(probability amplitude)」または省略して「振幅(amplitude)」と呼ぶことにした。つまり確率振幅は長さと方向をもつ「回転するベクトル」なのである。
ところで、光はガラスの表面だけでなくガラスの中を通過し、光源から見て裏面でも反射するはずだ。もし裏面でも4パーセント反射すると、表面の4パーセントの反射と合わせて合計8パーセント反射するはずだから、おかしなことになる。では表面と裏面でそれぞれ2パーセントずつ反射しているのだろうか?合わせて4パーセントになるからつじつまが合う。
そこで、実際にどうなるか実験をしてみた。ところが不思議なことがおきたのだ。ガラスの厚さを少しずつ変えながら赤と青の単色光で部分反射の実験をしてみると、次のような結果が得られた。横軸がガラスの厚さ、縦軸が反射率である。

ガラスの厚さが増えるにしたがい、反射率は0パーセントから16パーセントまでの間を周期的に変化する。赤色と青色ではその周期が2倍異なっている。いったい何がおきているのだろうか?この章では「矢印の計算」を紹介しながら、この不思議な現象のからくりを解き明かしている。ガラスによる光の反射と透過という日常みられる現象が、私たちが理解しているのとはまったく違うものであることがこの章で明らかにされるのだ。
2)光の粒子
この章では鏡による光の反射(光子の反射)が取り上げられる。Sから放出された光子は鏡の中央で反射してPに達する。このとき鏡の中央では入射角と反射角は等しくなる。だから光子の飛ぶ経路は、この図のようになるはずだ。

「入射角と反射角は等しい」ことは中学の理科で習うし、高校では幾何光学として習う。「ホイヘンスの原理」や「スネルの法則」のことである。
けれども、ここに重大な謎が潜んでいる。光子の経路がどのようにして決まったのかということだ。Sを出発した光子は鏡の中央を目指して飛んで行ったのだろうか?Sを出発したときに光子は鏡の中央を目指して飛びなさいと命令されていたのだろうか?または反射地点を知っていたのだろうか?中学と高校の理科では学んでいないはずである。
「ホイヘンスの原理」を一般化すると「フェルマーの原理(最小作用の原理)」が得られる。これは光は「目的地に最小時間で着くような経路を選ぶ」という原理だ。これで解決するだろうか?最小時間になるような経路を見つけるためには、目的地が決まっていなければならない。光子がSを出発したときに経由地(鏡の中央)や目的地Pを知っていたはずがない。
ファインマン先生も高校生のとき、この問題にとても興味を持っていた。そして先生がたどり着いたのが「光子は目的地に到達するために可能なあらゆる経路をとる」という結論だった。それはこのような図であらわされる。

この考えによればSから飛び出し、Aで反射してPに達する経路(SAP)や、同様にSBP、SCP、SDP、...、SMPの経路も「可能性として」考えられる。これらの経路を光子は「すべて」通っているのだと先生は考えた。たった1つの光子についてのことである。
そしてファインマン先生は、この現象を「矢印の足し算」として次のようにあらわした。

反射点が変わるとSからPまでの経路の長さ、すなわち光子がPに到達するまでの所要時間が変わる。SからPに到達するまでの所要時間を真ん中のグラフの縦軸にとると、図のようにU字型のグラフとなる。Pに向かって光子が進む間に「光の矢印」は回転しているから、Pに着いたときの矢印の向きは、グラフの縦の長さ(所要時間)によって違っている。
それぞれの反射点の下に光子ががPに到達したときの矢印を書く。そして最後にこれらの矢印のすべてを「ベクトルの足し算」として計算するのだ。するとその合計はいちばん下の太くて長い「最終矢印」となる。この最終矢印の長さの2乗が、この事象(光子がSからでて鏡で反射してPに到達する事象)が起きる確率とみなされる。光子は1つであっても鏡のAからMのすべての場所で反射しているのだ。
さて、この最終矢印の方向を決めるにあたって貢献度が高い小さな矢印はどれだろうか?小さい矢印をひとつずつ見てみると、鏡の中央に近い矢印が最終矢印と同じような向きであることがわかる。つまり、鏡の中央で反射するという現象がおきる確率を高めているのは、これら中央の矢印(確率振幅)たちなのである。
では、中央以外の矢印を考えなくてもよいのでは?と思うかもしれない。でもそれは違うのだ。実際に鏡の端に近い部分でも光子の反射がおきていることを、ファインマン先生は次の実験で示している。(この記事には書かないでおく。)ともかく、光子は鏡のあらゆるところで反射しているのだ。そして本書には書かれていないが、このような「可能なすべての経路の矢印を足し合わせる」ことを物理学では「経路積分」と呼んでいる。
この実験で考える「可能なすべての経路」とは、このようにぐにゃぐにゃ曲がった経路も合わせて計算するのだ。

私たちは、このように現象が起きる確率を通してしか自然の姿を見ることができない。これが量子電磁力学、量子力学が私たちに教えてくれることだ。
この章では鏡による反射の例に続いて、水中やガラスの中で光が遅くなるしくみ、水面やガラスの表面で光が屈折するしくみ、平行に入射した光がレンズで屈折して一点に集まるしくみ、光の回折がおきるしくみなどが矢印の計算方法を使って解説される。これらはすべて量子電磁力学によって解明された物理現象である。
3)電子とその相互作用
前の章では光の反射の現象を、経路積分を使ったマクロな視点から解説したが、この章ではこの現象を光子と電子の相互作用という素粒子の視点、ファインマン図を紹介しなから解説する。経路積分の考え方はファインマン図に活かされているのだ。
光子とは若干方法が異なるが、電子も同じように矢印を使って計算することができる。(詳細は本書で解説される。)
実をいうとガラスによる光子の部分反射は、鏡の表面と裏面だけでなく、ガラスの中全体でおきているのだ。このような図になる。矢印の足し算をして確率振幅の合計を求めると、不思議なことに表面と裏面だけで反射するときの結果と一致するのである。

そして、次に紹介されるのは光子が壁に衝突するボールのように反射しているのではないということなのだ。ガラス中の電子が入射してきた光子を吸収し、その後で電子が光子を放出する。つまり入射した光子と反射した光子は違う光子なのである。したがって電子と光子の相互作用を考えるのが反射、屈折、吸収などの光学現象を解き明かすカギとなる。たとえば、ファインマン図を使うと入射した光子が電子に吸収される現象はこの図のようにあらわされる。1と2を結ぶ直線が電子の経路、波線が光子の経路である。

ファインマン図では空間座標を横軸に、時間座標を縦軸にとっている。つまり特殊相対論の4次元時空内にあらわした素粒子の相互作用の図なのだ。ファインマン図では線と点の結びつき方が同じものを同一視する。マクロな世界の光子の経路のように曲線を描いたりすることは考慮しない。
4次元時空内で可能な経路というものを考えてみよう。これは時刻0にS(Start)の位置にある電子が、時刻7にG(Goal)の位置に達するという状況だ。可能な経路は無数あるのだが、ここには赤、青、緑の3つの経路だけ描いておいた。

ここで青の経路に注目してほしい。Sから右下に伸びている矢印は、空間座標は増えているものの、時刻は0からマイナス2に減っている。電子が時間を逆行しているのだ。特殊相対論を満たしている経路積分では時間をさかのぼる経路も「可能な経路」のうちに含めて考える。
けれども、物理法則は時間をさかのぼるタイムトラベルを禁じている。物事の因果関係が崩壊してしまうからだ。物事の原因は結果よりも必ず先に起きなければならない。因果関係が逆転すると入学試験を受ける前に合格通知が届くようなことになってしまう。
ファインマン図、量子電磁力学ではこの矛盾を、反粒子を使って解決している。理論上「時間を逆行する電子」は「時間を順行する陽電子」に同一視されるからだ。電子の反粒子は陽電子、そして光子の反粒子は光子である。
左側の図は、未来からやってきた光子が過去から来た電子とぶつかり、電子が向きを変えて未来から過去へとさかのぼっていく様子ともとらえることができる。同様に右側の図は光子から、未来へ飛んでいく電子と過去へ飛んでい電子が対生成される様子である。

この考え方に従えば、未来からやってきた光子を「未来へ飛んでいく光子」、過去へさかのぼる電子を「未来へ飛んでいく陽電子」と考え、つじつまが合って因果関係が保たれる。
次にファインマン図を使った量子電磁力学の最大の成果、つまり電子の磁気モーメントの値を極めて正確に計算できたことが解説される。理論値と実験値がとてつもなく高い精度で一致したことが、量子電磁力学の正しさを裏付けることになった。
再掲するが、ディラックが電子の磁気モーメントを1だと計算したときのファインマン図はこのようなものである。

この4次元時空で可能なあらゆる経路というのは、ファインマン図で電子のスタート地点とゴール地点が一致しているという条件だけでなく、電子の放出や吸収など可能なあらゆる事象も考慮されることになるのだ。つまり、上の図を1次の相互作用の図とすれば、2次、3次、3次...と段階的に複雑な事象を描いたファインマン図を使って近似の計算精度を上げていく。たとえば上と同じ事象であっても、次のような図であらわされることになる。

電子の場合、この段階的な近似計算は、驚くほど速く数値が収束していく。計算方法は本書で詳しく解説している。このような計算を経て電子の磁気モーメントの値が高い精度で求められていったのだ。その結果、磁気モーメントの値は1ではなく、理論値は1.00115965246、実験値は1.00115965221となった。末尾の桁には±4くらいの誤差がある。
確率振幅を意味する「矢印」は光子や電子ひとつひとつに紐づいているのではないことを強調しておこう。粒子が複数あれば、複数の粒子の状態に対して1本の矢印が紐づいている。複数の初期状態から最終状態に至る矢印の長さの2乗がその物理現象が起きる確率であると考えるのだ。
確率振幅(矢印)は向きと長さをもったベクトルである。それは複素平面上にある矢印とみなすことができる。つまり確率振幅は複素数の値をとる。電子についてのシュレディンガー方程式に含まれる波動関数も複素数の値をとり、これは確率振幅とみなされている。波動関数の2乗が電子の存在確率であるというのが「ボルンの確率解釈」だ。つまりこれまでの説明で、矢印の長さを2乗するということは、その物理現象がこの世界に実体化する確率を求めていたのである。
また、矢印の計算は可能な経路を計算するときは足し算、時間の経過に従った2つの事象を計算するときは掛け算になるということを補足しておこう。
電子はすべての物質に含まれている粒子である。電子と光子の相互作用を解き明かす量子電磁力学は、この世界のほとんどの物質現象の基礎とみなされている。原子や分子の化学結合、化学反応、絶縁体と導電体、物質が透明か不透明か、空が青い理由、なぜテーブルや机が硬いのか、物にさまざまな色があること、燃やすとなぜ炎がでるのかなどは、すべて量子電磁力学がもとになって生じている。
矢印の計算は「光子の作用」、「電子の作用」、「光子と電子の相互作用」の3種類しかない。自然が私たちに見せる多様性のほとんどが、量子電磁力学の3種類の原理がもとになっているのである。
4)未解決の部分
第4章では電子と光子の後に発見された素粒子について解説する。原子核を構成する陽子や中性子は、根源的な素粒子ではなくクォークから構成されていることがわかった。量子電磁力学の矢印の計算による手法は、原子核の中の粒子についても10パーセントという精度で成り立つことが示された。しかし、その誤差は原子核内の物理学が電子や光子の物理学と本質的に違うことを意味している。
ただしファインマン図や経路積分は原子核内の素粒子に対しても有用なツールであり、たとえばクォークを含んだ相互作用では次のような図を使って計算が行われている。経路積分の手法は「シュレーディンガー方程式」や「ハイゼンベルクの運動方程式」と数学的に同等であることがダイソンによって証明された。これは経路積分やファインマン図の手法の有効性を裏付けるものだ。そして量子力学は原子核の中でも成り立っているのである。

ファインマン図については、この動画で理解するとよいだろう。
【3分解説】ファインマン図
そしてこの章では素粒子物理学の発展史が順に解説される。この本が出版された1986年であるから、1995年に発見されたトップクォーク、そして2012年に発見されたヒッグス粒子は言及されていない。1986年の時点では電弱理論、量子色力学(強い相互作用)までである。あとニュートリノの質量もゼロだとされていた。(実際にはわずかながら質量があることがその後確認された。)繰り込み理論は軽く紹介されていた。

本書の一部だけをかいつまんで紹介させていただいた。ファインマン先生の著書、講義はどれをとってもエキサイティングだ。読む者、聴く者の心をつかみ、理路整然と続ける話の中で先入観や誤解を溶かし、まったく思いがけない世界へ私たちを導いてくれる。このようなスタイルで物理学や数学を語れるような人になりたいと、つくづく思ってしまうのだ。
英語版と日本語版について
科学英語の読解トレーニングにはうってつけの本だと思った。主題は光子と電子、その他の素粒子だけであること、計算の方法も一貫しているから、英文のパターンも限られている。読んでいくうちに慣れてくるからスピードも上がる。
日本語版は薄い文庫本だが、英語で読むと4日かかった。英語だと一字一句精読することになるから書かれていることをすべて吸収できる。僕がどれだけ熱中していたかは「この連投ツイート」をご覧になればおわかりになると思う。
英語版はファインマン先生の姿が載っている2006年版をKindle端末で読んだ。1988年に亡くなったファインマン先生が手にしたのは1986年版である。そしていちばん新しいのが2014年に刊行されている。
「QED: The Strange Theory of Light and Matter (2006): Richard P. Feynman」
(Kindle版)(2014)(1986)



日本語版はこの2冊。1986年の英語版が刊行されてすぐ、ファインマン先生が大貫昌子さんを翻訳者に指名したという。大貫さんは「ご冗談でしょう、ファインマンさん」を訳して先生の信頼を得ていたからだ。先生は1987年に刊行された日本語訳(単行本)を手にしてお喜びになったに違いない。
「光と物質のふしぎな理論―私の量子電磁力学 (文庫、2007): R.P.ファインマン」(紹介記事)
「光と物質のふしぎな理論―私の量子電磁力学 (単行本、1987): R.P.ファインマン」


講義の動画、リスニングのトレーニング
この本の元になった講義は1979年と1983年に行われたようだ。1979年に行われた講義は、こちらからご覧いただける。本を読んでからだと講義がわかりやすい。(動画を検索)
QED: Photons-Corpuscles of Light (Richard Feynman 1/ 4)
第1回 第2回 第3回 第4回 プレイリスト The Vega Science Trustの公開動画
各回の講義の後に行われた質疑応答が素晴らしい。本には書かれていないことについて、興味深い話を先生はたくさんお話しになっている。
1983年に行われた講義もYouTubeでご覧いただける。こちらのほうが画質がよい。本書の内容は第2回から始まる。
Richard Feynman: Quantum Mechanical View of Reality 1
第1回 第2回 第3回 第4回
NHKにはファインマン先生をCGで蘇らせて、この4回にわたる名講義を再現した科学番組を作ってもらいたいと思うのだ。また、ニュートンプレス社には本書の内容を「別冊ニュートン」として刊行してもらいたいとも思った。テーマがテーマだけにビジュアルなイラストで魅力的な紙面が満載の本になると思う。
次の動画は本書の内容に沿っているのでお勧めだ。光のガラスによる部分反射の実験と鏡による反射の実験、ファインマン図を使って光子と電子の相互作用を解説している。英語字幕付きなのでリスニングの練習用に使ってもよいだろう。英語がわからなくても見ているだけで楽しめると思う。
Quantum Electrodynamics
経路積分とファインマン図は、次の動画で学ぶとよい。とても詳しく解説している。
Feynman's Infinite Quantum Paths | Space Time(経路積分の解説動画)
The Secrets of Feynman Diagrams | Space Time(ファインマン図の解説動画)
この2つの動画は「量子力学の再生リスト」の一部である。
ファインマン先生による量子電磁力学の教科書
ファインマン先生は量子電磁力学の教科書をお書きになっている。アマゾンから販売されているほか、著作権切れであるため無料で読むこともできる。
「Quantum Electrodynamics: Richard P. Feynman」(Kindle版)

無料版(1961年刊行):
Quantum Electrodynamics - R.P. Feynman (PDF)
https://archive.org/details/QuantumElectrodynamics/page/n49
フランス語版とドイツ語版
熱が入ってフランス語版を注文してしまった。届いたら通読してみたい。(通読中の連投ツイート)(紹介記事)
「Lumière et matière - Une étrange histoire: Richard P. Feynman」(Amazon.fr)
「QED: Die seltsame Theorie des Lichts und der Materie: Richard P. Feynman」(Kindle版)


フランス語の内容紹介:
" Et maintenant, attachez vos ceintures. Non pas que ce soit particulièrement difficile à comprendre, mais tout simplement parce que ça va vous sembler le comble du ridicule. Jugez-en : nous dessinons des petites flèches sur une feuille de papier ! C'est tout. "
L'électrodynamique quantique, qui décrit les interactions entre lumière et matière, prototype des théories de la physique moderne, devient un jeu d'enfant quand elle est expliquée par un de ses créateurs. Richard Feynman montre que les notions les plus difficiles sont explicables sans formalisme mathématique et que leur sens profond est à la portée de tous.
Un sommet de la vulgarisation scientifique.
ドイツ語の内容紹介:
Der amerikanische Physiker Richard P. Feynman galt als einer der größten theoretischen Physiker dieses Jahrhunderts. Für seine Beiträge zur Theorie der Quantenelektrodynamik erhielt er 1965 (mit zwei Kollegen) den Nobelpreis für Physik. Mit dieser Quantenelektrodynamik – kurz QED – befasst sich dieses Buch, in dem er erklärt: "Mein Hauptanliegen ist, die seltsame Theorie des Lichts und der Materie, oder richtiger die Wechselwirkung zwischen Licht und Elektronen, so genau wie möglich zu beschreiben." Der Leser wird Feynmans lebendige und unterhaltsame Art der Darstellung genießen, wenn ihm der berühmte Physiker und begabte Lehrer eine des maßgeblichen physikalischen Theorien dieses Jahrhunderts erklärt.
関連記事:
光と物質のふしぎな理論―私の量子電磁力学: R.P.ファインマン
https://blog.goo.ne.jp/ktonegaw/e/4b34cd4e7d077d037022e62734d1ee76
Lumière et matière - Une étrange histoire: Richard P. Feynman(光と物質のふしぎな理論)
https://blog.goo.ne.jp/ktonegaw/e/625073adb96b546870720092abd5158d
ファインマンの経路積分に入門しよう!
https://blog.goo.ne.jp/ktonegaw/e/0f47de5854daf4eb38339a73791544a8
ファインマン先生の自伝本と講演本
https://blog.goo.ne.jp/ktonegaw/e/9bf47cf51085c74caf34a11068a17285
ファインマン物理学(英語版)が全巻ネット公開されました。
https://blog.goo.ne.jp/ktonegaw/e/e94dd49d7d8cc395e29d37927e30173d
万有引力の法則(逆2乗則)の逆問題を解説する本と動画(ファインマンによる解法)
https://blog.goo.ne.jp/ktonegaw/e/2cd381bca4546d23968b31cfad4a9be9
開平と開立(第5回): ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb
#Feynman100: ファインマン先生、生誕100周年セレモニー&シンポジウム
https://blog.goo.ne.jp/ktonegaw/e/11dd9238ebcbc37915920a2dab553c82
強い力と弱い力:大栗博司(標準模型について学べる科学教養書)
https://blog.goo.ne.jp/ktonegaw/e/06c3fdc3ed4e0908c75e3d7f20dd7177
メルマガを書いています。(目次一覧)

応援クリックをお願いします。


























