
「ポアンカレ 常微分方程式 -天体力学の新しい方法-」
内容紹介:
ポアンカレの名著『天体力学の新しい方法』の第3巻の全訳。
積分不変式・積分不変式の形成・積分不変式の用法・積分不変式と漸近解・後継点の理論・第二種周期解他。1975年以降「カオス」と呼ばれるようになった力学系の複雑極まる現象を、世界で初めて数学的に発見したことが書かれている。
1970年9月10日刊行、438ページ。
著者について:
ジュール=アンリ・ポアンカレ(Jules-Henri Poincaré、1854年4月29日 – 1912年7月17日):ウィキペディア
ナンシー生まれのフランスの数学者、理論物理学者、科学哲学者。数学、数理物理学、天体力学などの重要な基本原理を確立し、功績を残した。フランス第三共和制大統領・レーモン・ポアンカレはアンリの従弟(いとこ)。
ポアンカレの著書、ポアンカレ関連の本: Amazonで検索
理数系書籍のレビュー記事は本書で395冊目。
中身を確認しないで注文した。数分ながめただけで、すべて解読できる本ではないことがわかった。けれども文章が多いようだから何について書いているか、ポアンカレの思考の流れはつかめるかもしれないと思い、時間をかけて通読してみた。
「天体力学のパイオニアたち 上: F.ディアク、R.ホームズ」という先日紹介した本の第1章で解説されていたのが『天体力学の新しい方法(Les Méthodes Nouvelles de la Mécanique Céleste)』である。
微分方程式の新しい解法を論じ、これを天体力学に応用する中で、1975年以降「カオス」と呼ばれるようになった力学系の複雑極まる現象を、世界で初めて数学的に発見したことが書かれている本だ。
スウェーデン王、オスカー3世は、1889年に満60歳になる機会に数学解析の領域における重要な発見に授賞するために論文を募集した。ワイエルシュトラス、エルミート、ミッタグ-レフラーからなる審査員は4つの問題を提出し、応募者はそのうちのひとつを選ぶことができた。
提案された4つの問題はどれもポアンカレにとっては興味あるものだったが、彼はその中で最も困難と思われる第1の問題(N体問題の一般解を求める方法)を選び、彼はこの論文によって1889年に受賞した。それは「三体問題と力学の方程式について」である。彼は1890年ごろから天体力学の研究を展開していたが、その成果は1892年、1893年、1899年に『天体力学の新しい方法』の第1巻、第2巻、第3巻として出版された。
日本語版は「現代数学の系譜(Amazonで検索)」シリーズの1冊として1970年に刊行された。この日本語版はフランス語版の第3巻の翻訳に第1巻の抄訳を補遺として付けたものである。補遺は第3巻を理解するのに必要な最低限のことを第1巻から抜粋したものだ。フランス語版第1巻、第1章のn°8-n°13、すなわち「ケプラー運動」、「制限3体問題」、「一般3体問題」、「力学の一般的な問題」のハミルトン系の正準方程式による立式、ベキ級数展開が解説されている。フランス語版の第1巻と第2巻の全訳の日本語版は刊行されていない。
『天体力学の新しい方法』の3巻が数学理論であるのに対して、彼は次にもっと実用的な『天体力学講義(Leçons de Mécanique Céleste)』を執筆。第1巻を1905年、第2巻は2冊で1907年と1908年に、第3巻は1910年に出版された。(ポアンカレの没年は1912年である。)
『天体力学の新しい方法』は、1889年に受賞した研究を発展させたものである。『天体力学講義』のほうはより実用的で、その第1巻と第2巻は特に摂動論を展開し、第2巻2節で月の運動を論じている。第3巻では数学的な取り扱いがさらに困難な潮汐が天体の回転に及ぼす影響について論じている。
『天体力学の新しい方法』には図版がほんのわずかしかない。天体の軌道や方程式があらわす曲線図形はポアンカレの頭の中に描かれている。これが文章で表現されたものを読者は理解しなければならないから、とても読みにくい。エコール・ポリテクニクに入学する時、ポアンカレは図画の試験で0点を取り、入学許可のための特例措置がとられたという。これは本書に図版が少ないことの理由のひとつかもしれない。図版不足を補うために、この記事では「天体力学のパイオニアたち 上: F.ディアク、R.ホームズ」から図版を拝借して載せることにしよう。
ポアンカレの学位論文は、1878年にパリ大学に提出された『微分方程式によって定義される関数の性質について』である。審査員の一人、G.ダルブーの言葉をかりれば「彼は直観派である。一度頂上に達すると決して二度と下には戻ってこない。」ということ。そして本書を翻訳した数学者の福原満洲雄先生は「彼の証明はときにはなはだ不十分である。計算にも誤りが多い。それにもかかわらず、結果の見通しを誤らない。そこに彼の非凡な洞察力を見ることができる。」とお書きになっている。手取り足取り教えてくれる教科書ではないのだ。
『天体力学の新しい方法』の第3巻、すなわち「ポアンカレ 常微分方程式 -天体力学の新しい方法-」の目次は次のとおり。第22章から始まる。フランス語の原書のほうには目次はない。当時の製版、製本の手順で目次や索引をつくるのは難しいためだと思われる。
第22章:積分不変式
第23章:積分不変式の形成
第24章:積分不変式の用法
第25章:積分不変式と漸近解
第26章:ポアソン安定
第27章:後継点の理論
第28章:第二種周期解
第29章:最小作用原理の諸形式
第30章:第二種解の作り方
第31章:第二種周期解の性質
第32章:第二部類の周期解
第33章:二重漸近解
補遺
1.ケプラー運動
2.制限三体問題
3.ケプラー変数の用法
4.一般三体問題
5.力学の一般的な問題
微分方程式の解法には、まず有限回の不定積分を使って厳密に解ける「求積法」があり、これは大学1、2年で学ぶ。(参考記事:「ちょっと気になる常微分方程式の本」)求積法で解けない問題は近似的に解く「摂動法」と呼ばれる級数を使う解法が知られている。しかし、3体問題は摂動法でも解けず、新たな概念を導入する必要があった。それが「積分不変式」や「偏差方程式」、「特性指数」である。本書の第22章から第25章まではこの解説にあてられる。ポアンカレは常微分方程式の周期解の一般論の研究から始めて、3体問題への応用を試みた。
一般の3体問題は求積法や摂動法では解くのが不可能であるだけでなく、ポアンカレのアイデアを使っても計算が難しすぎる。解きやすくするために彼は条件に制限をつけた。彼が設定した「制限3体問題」は、平面上で楕円軌道(ケプラー軌道)を描いて運動する大質量の2つの惑星と微小質量の3つめの惑星が繰り広げる運動のことである。

ポアンカレの計算は、この系のある平衡解のまわりで「2重漸近解」を発生し得ることを示した。この図のように平衡点を離れて、時間の増大とともに再び漸近的に平衡点に戻る曲線で、同一の極限から発してふたたび平衡点に向かう軌道には「ホモクリニック軌道」、2つの異なる平衡点を結ぶ軌道には「ヘテロクリニック軌道」という名前をつけた。

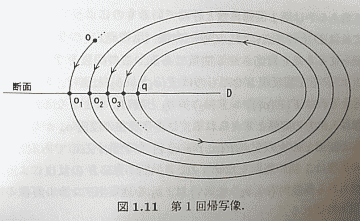
また、3つめの「周期軌道」のグループには渦巻きのように中心に向かう軌道と渦巻きながら外側に向かう軌道がある。この軌道を数学的に取り扱いやすくするために「第1回帰写像(ポアンカレ写像)」というアイデアを用いた。解曲線の全体は断面を横切る点列であらわされることになる。こうすることで2次元の問題が1次元の問題に帰着される。この点集合は「不変曲線」と呼ばれる。
物理学では現実の空間を離れた数学の世界の「相空間」を使って計算することが多い、周期的な相空間は下の左図のようなもので、t=0からt=Tで繰り返す平面を同一視すれば右図のようにあらわされ、これがポアンカレ写像ということになる。

説明を端折らせていただくが、この図の中の写像は点列を番号の順に写し、2次元の「安定多様体」と「不安定多様体」はポアンカレ写像に対する2つの不変曲線(SとU)になる。不安定な周期運動は、正確に周期Tで繰り返すので、写像に対する不動点として現れる。曲線SとUはこの周期運動の安定および不安定多様体に属する。SとUは、単一の滑らかな曲線とは違い、2つの異なる曲線として断面上に現れ、ある特殊な軌道に対しては2つの曲線が交わることになる。点列はnが無限に大きくなるとき不動点に接近する。ホモクリニックな交点はSにもUにも属するので、それが1つあると、無限に多くホモクリニック点を生み出す。これがポアンカレの「2重漸近」である。ホモクリニック点列から1次のホモクリニック軌道が生じ(説明省略)、2次、3次、4次...のホモクリニック軌道が生成される。
安定多様体Sと不安定多様体Uの1つの交点から出発して、そのような無限個の族が構成され、これらの点は曲線をホモクリニック・タングル(絡み)という一種の網、格子のようなものに貼り付けてしまう。網のすべての糸はSまたはUに属する弧であり、これらの糸は未来において最終的に鞍点(図のp)の左か右を通過する軌道を分離する。相空間の有限の領域に無限の「分離」が詰め込まれた状態だ。この状況はどのように与えられた初期条件から出発した軌道であっても、その未来を予測することは現実的に不可能になる。このホモクリニック・タングルは、今日カオスと呼ばれる現象の、最初の数学的な出現だったのだ。

このカオスの存在にに気がついたポアンカレの驚きは、本書の次のような記述でうかがい知ることができる。
拡大

拡大

「三体問題がいかに複雑なものか、またこの問題を解くためには、われわれの既知のすべての知識とは異なった超越的な知識が、いかに必要であるかもわかってくる。」
「その複雑さは驚くべきもので、私自身もこの図形を引いてみせようとは思わない。三体問題の複雑さに、もっと一般には、一価の積分をもたず、ボーリン(Bohlin)の級数が収束しないような、すべての力学の問題の複雑さに、なにかの概念を与えてくれるもの、またはそれに適したものは、これ以上なにもない。」
なお、本書の補遺は第3巻を理解するのに必要な最低限のことを第1巻から抜粋したものだが、実際のところ第1巻の他の章や第2巻の記述を参照せよとしている箇所がいくつも見られ、論理的な整合性を大切にして読むのであれば第1巻と第2巻は必須である。
第1巻では第1種の周期解の研究と、一価正則な積分の不存在の証明、永年項に関すること、そしてリントシテットによる方法の記述と解説にあてられている。第2巻と第3巻は、ギルデンによる方法の議論と、安定性の問題、第2種周期解および漸近解、二重漸近解の研究が解説されている。
ポアンカレは本書を『天体力学の新しい方法』と名付けたが、取り上げている3体問題は実際の惑星の運動ではほぼあり得ず、数学的な研究であるとしているが、正三角形解と直線解を導いた3体問題のラグランジュ解がトロヤ群と呼ばれる小惑星群として発見され安定な正三角形解の存在が裏付けられた。また、一般に3体問題はニュートン力学であるが、近年研究されている天の川銀河の中心のブラックホールSgr A*を周回する恒星の群れなどは、一般相対性理論を使って解くべき多体問題だ。(動画の引用元のページ)3体問題や多体問題(N体問題)はもはや数学の世界だけの話ではない。

この日本語版が刊行されたのは1970年、先日「映画『ファースト・マン(2018)』」として紹介したアポロ11号の翌年、大阪万博や三島事件があった年である。ポアンカレ以降50年経った1960年代からカオスは数学的な発展を再開したのだが、ウィキペディアの「カオス理論」という記事によると「この複雑な軌道の概念は1975年、ジェイムズ・A・ヨークとリー・ティエンイエンによりカオスと呼ばれるようになった。」ということだそうである。本書巻末の「解説」ではポアンカレの微分方程式論やトポロジー分野への功績の記述がほとんどで、彼がカオスを最初に垣間見たことに言及していないのはそのためである。原書タイトルにはない「常微分方程式」を日本語版の主タイトルにしたのも同じ理由だと思われる。
3体問題の動画は見ていて飽きない。3つ紹介しておこう。
非周期的(カオス)で3次元の3体問題
解の初期値鋭敏性が確認できる動画。開始2分あたりから軌道が分岐する。
周期解ばかりを集めたもの。とても面白い。
3体問題の動画: YouTubeで検索
原書のフランス語版は、昨年新装版が発売されたばかりだ。アマゾンジャパンから買うことができる。
「Les Méthodes Nouvelles de la Mécanique Céleste, Vol. 1: Henri Poincaré」(1892)
「Les Méthodes Nouvelles de la Mécanique Céleste, Vol. 2: Henri Poincaré」(1893)
「Les Méthodes Nouvelles de la Mécanique Céleste, Vol. 3: Henri Poincaré」(1899)



このフランス語版は3冊とも無料で公開されている。オンライン、PDFのほか各種フォーマットで閲覧できる。
オンライン閲覧:第1巻、第2巻、第3巻
セピア色のPDF: 第1巻、第2巻、第3巻
白黒のPDF: 第1巻、第2巻、第3巻
もちろん英語版も刊行されているが、高過ぎてお勧めできない。: Amazonで検索
より実用的な『天体力学講義(Leçons de Mécanique Céleste)』のフランス語版も新装版として昨年刊行されている。アマゾンジャパンから買うことができる。1912年に亡くなったポアンカレ最晩年の著作だ。英語や日本語には翻訳されていない。
「Leçons de Mécanique Céleste, Vol. 1: Henri Poincaré」(1905)
「Leçons de Mécanique Céleste, Vol. 2: Henri Poincaré」(1907, 1908)
「Leçons de Mécanique Céleste, Vol. 3: Henri Poincaré」(1910)



このフランス語版も無料で公開されている。オンライン、PDFのほか各種フォーマットで閲覧できる。
オンライン閲覧:第1巻、第2巻、第3巻
セピア色のPDF: 第1巻、第2巻、第3巻
白黒のPDF: 第1巻、第2巻、第3巻
今回の記事の続きは「ポアンカレによるカオスの発見と先見性」として補足している。合わせてお読みいただきたい。
関連記事:
ポアンカレによるカオスの発見と先見性
https://blog.goo.ne.jp/ktonegaw/e/daf1e56d0751c928592e75282d69835e
天体力学のパイオニアたち 上: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/5c51d50e2141c8ae58c9323ad49b65a1
天体力学のパイオニアたち 下: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/88846fbb12ed1f8b11a49f0659b93c75
数理解析のパイオニアたち: V.I.アーノルド
https://blog.goo.ne.jp/ktonegaw/e/165c894d023b1174fd519522935cdeeb
Hirsch・Smale・Devaney 力学系入門 ―微分方程式からカオスまで― 第3版
https://blog.goo.ne.jp/ktonegaw/e/98d451af90b7efc63aacbe4efdb330fa
力学系カオス: 松葉育雄
https://blog.goo.ne.jp/ktonegaw/e/12392ac282d10deed28914d8182c2286
古典力学の形成―ニュートンからラグランジュへ:山本義隆
https://blog.goo.ne.jp/ktonegaw/e/e808487b7e9d668967f703396e32d80a
全5巻完結!:ラプラスの天体力学論(日本語版)
https://blog.goo.ne.jp/ktonegaw/e/a720b0cfb775d00625763f87a56b2414
発売情報: 惑星探査機の軌道計算入門: 半揚稔雄
https://blog.goo.ne.jp/ktonegaw/e/a3aba0b87bff8a8ae54fb37ad1b04504


「ポアンカレ 常微分方程式 -天体力学の新しい方法-」

第22章:積分不変式
- 定常状態にある流体の運動
- 積分不変式の定義
- 不変式と積分の関係
- 相対不変式
- 不変式と偏差方程式の関係
- 不変式の変換
- 不変式と積分との間の他の関係
- 変数変換
- 諸注意
第23章:積分不変式の形成
- 積分因子の用法
- 力学の方程式
- 積分不変式と特性指数
- ケプラー変数の用法
- n°256の不変式に関する注意
- 縮減三体問題の場合
第24章:積分不変式の用法
- 検算法
- ヤコビの定理との関係
- 二体問題への応用
- 漸近解への応用
第25章:積分不変式と漸近解
- ボーリンの方法(再)
- 積分不変式との関係
- 別の論法
- 2次型不変式
- 制限問題の場合
第26章:ポアソン安定
- 安定性の諸定義
- 液体の運動
- 確率
- 諸結果の拡張
- 制限問題への拡張
- 三体問題への応用
第27章:後継点の理論
- 後継点の理論
- 不変曲線
- 諸結果の拡張
- 力学の方程式への応用
- 制限問題への応用
第28章:第二種周期解
- 第二種周期解
- 時間が陽に現われない場合
- 力学の方程式への応用
- 力学の方程式の第二種解
- 極大に関する諸定理
- 第二種解の存在
- 注意
- 特別の場合
第29章:最小作用原理の諸形式
- 最小作用原理の諸形式
- 運動学的焦点
- モーペルチュイ焦点
- 周期解への応用
- 安定解の場合
- 不安定解
第30章:第二種解の作り方
- 第二種解の作り方
- 解の効果的な作り方
- ディスカッション
- 特別な場合のディスカッション
- n°13の方程式への応用
第31章:第二種周期解の性質
- 第二周期解と最小作用の原理
- 安定と不安定
- ダーウィン軌道への応用
第32章:第二部類の周期解
- 第二部類の周期解
第33章:二重漸近解
- 種々の幾何学的表現法
- ホモクリーヌな解
- ヘテロクリーヌな解
- n°225(第2巻)との比較
- ヘテロクリーヌな解の例
補遺
1.ケプラー運動
2.制限三体問題
3.ケプラー変数の用法
4.一般三体問題
5.力学の一般的な問題
解説
1.Henri Poincaré について
2.常微分方程式論について
3.三体問題と常微分方程式論
年表
内容紹介:
ポアンカレの名著『天体力学の新しい方法』の第3巻の全訳。
積分不変式・積分不変式の形成・積分不変式の用法・積分不変式と漸近解・後継点の理論・第二種周期解他。1975年以降「カオス」と呼ばれるようになった力学系の複雑極まる現象を、世界で初めて数学的に発見したことが書かれている。
1970年9月10日刊行、438ページ。
著者について:
ジュール=アンリ・ポアンカレ(Jules-Henri Poincaré、1854年4月29日 – 1912年7月17日):ウィキペディア
ナンシー生まれのフランスの数学者、理論物理学者、科学哲学者。数学、数理物理学、天体力学などの重要な基本原理を確立し、功績を残した。フランス第三共和制大統領・レーモン・ポアンカレはアンリの従弟(いとこ)。
ポアンカレの著書、ポアンカレ関連の本: Amazonで検索
理数系書籍のレビュー記事は本書で395冊目。
中身を確認しないで注文した。数分ながめただけで、すべて解読できる本ではないことがわかった。けれども文章が多いようだから何について書いているか、ポアンカレの思考の流れはつかめるかもしれないと思い、時間をかけて通読してみた。
「天体力学のパイオニアたち 上: F.ディアク、R.ホームズ」という先日紹介した本の第1章で解説されていたのが『天体力学の新しい方法(Les Méthodes Nouvelles de la Mécanique Céleste)』である。
微分方程式の新しい解法を論じ、これを天体力学に応用する中で、1975年以降「カオス」と呼ばれるようになった力学系の複雑極まる現象を、世界で初めて数学的に発見したことが書かれている本だ。
スウェーデン王、オスカー3世は、1889年に満60歳になる機会に数学解析の領域における重要な発見に授賞するために論文を募集した。ワイエルシュトラス、エルミート、ミッタグ-レフラーからなる審査員は4つの問題を提出し、応募者はそのうちのひとつを選ぶことができた。
提案された4つの問題はどれもポアンカレにとっては興味あるものだったが、彼はその中で最も困難と思われる第1の問題(N体問題の一般解を求める方法)を選び、彼はこの論文によって1889年に受賞した。それは「三体問題と力学の方程式について」である。彼は1890年ごろから天体力学の研究を展開していたが、その成果は1892年、1893年、1899年に『天体力学の新しい方法』の第1巻、第2巻、第3巻として出版された。
日本語版は「現代数学の系譜(Amazonで検索)」シリーズの1冊として1970年に刊行された。この日本語版はフランス語版の第3巻の翻訳に第1巻の抄訳を補遺として付けたものである。補遺は第3巻を理解するのに必要な最低限のことを第1巻から抜粋したものだ。フランス語版第1巻、第1章のn°8-n°13、すなわち「ケプラー運動」、「制限3体問題」、「一般3体問題」、「力学の一般的な問題」のハミルトン系の正準方程式による立式、ベキ級数展開が解説されている。フランス語版の第1巻と第2巻の全訳の日本語版は刊行されていない。
『天体力学の新しい方法』の3巻が数学理論であるのに対して、彼は次にもっと実用的な『天体力学講義(Leçons de Mécanique Céleste)』を執筆。第1巻を1905年、第2巻は2冊で1907年と1908年に、第3巻は1910年に出版された。(ポアンカレの没年は1912年である。)
『天体力学の新しい方法』は、1889年に受賞した研究を発展させたものである。『天体力学講義』のほうはより実用的で、その第1巻と第2巻は特に摂動論を展開し、第2巻2節で月の運動を論じている。第3巻では数学的な取り扱いがさらに困難な潮汐が天体の回転に及ぼす影響について論じている。
『天体力学の新しい方法』には図版がほんのわずかしかない。天体の軌道や方程式があらわす曲線図形はポアンカレの頭の中に描かれている。これが文章で表現されたものを読者は理解しなければならないから、とても読みにくい。エコール・ポリテクニクに入学する時、ポアンカレは図画の試験で0点を取り、入学許可のための特例措置がとられたという。これは本書に図版が少ないことの理由のひとつかもしれない。図版不足を補うために、この記事では「天体力学のパイオニアたち 上: F.ディアク、R.ホームズ」から図版を拝借して載せることにしよう。
ポアンカレの学位論文は、1878年にパリ大学に提出された『微分方程式によって定義される関数の性質について』である。審査員の一人、G.ダルブーの言葉をかりれば「彼は直観派である。一度頂上に達すると決して二度と下には戻ってこない。」ということ。そして本書を翻訳した数学者の福原満洲雄先生は「彼の証明はときにはなはだ不十分である。計算にも誤りが多い。それにもかかわらず、結果の見通しを誤らない。そこに彼の非凡な洞察力を見ることができる。」とお書きになっている。手取り足取り教えてくれる教科書ではないのだ。
『天体力学の新しい方法』の第3巻、すなわち「ポアンカレ 常微分方程式 -天体力学の新しい方法-」の目次は次のとおり。第22章から始まる。フランス語の原書のほうには目次はない。当時の製版、製本の手順で目次や索引をつくるのは難しいためだと思われる。
第22章:積分不変式
第23章:積分不変式の形成
第24章:積分不変式の用法
第25章:積分不変式と漸近解
第26章:ポアソン安定
第27章:後継点の理論
第28章:第二種周期解
第29章:最小作用原理の諸形式
第30章:第二種解の作り方
第31章:第二種周期解の性質
第32章:第二部類の周期解
第33章:二重漸近解
補遺
1.ケプラー運動
2.制限三体問題
3.ケプラー変数の用法
4.一般三体問題
5.力学の一般的な問題
微分方程式の解法には、まず有限回の不定積分を使って厳密に解ける「求積法」があり、これは大学1、2年で学ぶ。(参考記事:「ちょっと気になる常微分方程式の本」)求積法で解けない問題は近似的に解く「摂動法」と呼ばれる級数を使う解法が知られている。しかし、3体問題は摂動法でも解けず、新たな概念を導入する必要があった。それが「積分不変式」や「偏差方程式」、「特性指数」である。本書の第22章から第25章まではこの解説にあてられる。ポアンカレは常微分方程式の周期解の一般論の研究から始めて、3体問題への応用を試みた。
一般の3体問題は求積法や摂動法では解くのが不可能であるだけでなく、ポアンカレのアイデアを使っても計算が難しすぎる。解きやすくするために彼は条件に制限をつけた。彼が設定した「制限3体問題」は、平面上で楕円軌道(ケプラー軌道)を描いて運動する大質量の2つの惑星と微小質量の3つめの惑星が繰り広げる運動のことである。

ポアンカレの計算は、この系のある平衡解のまわりで「2重漸近解」を発生し得ることを示した。この図のように平衡点を離れて、時間の増大とともに再び漸近的に平衡点に戻る曲線で、同一の極限から発してふたたび平衡点に向かう軌道には「ホモクリニック軌道」、2つの異なる平衡点を結ぶ軌道には「ヘテロクリニック軌道」という名前をつけた。

また、3つめの「周期軌道」のグループには渦巻きのように中心に向かう軌道と渦巻きながら外側に向かう軌道がある。この軌道を数学的に取り扱いやすくするために「第1回帰写像(ポアンカレ写像)」というアイデアを用いた。解曲線の全体は断面を横切る点列であらわされることになる。こうすることで2次元の問題が1次元の問題に帰着される。この点集合は「不変曲線」と呼ばれる。

物理学では現実の空間を離れた数学の世界の「相空間」を使って計算することが多い、周期的な相空間は下の左図のようなもので、t=0からt=Tで繰り返す平面を同一視すれば右図のようにあらわされ、これがポアンカレ写像ということになる。

説明を端折らせていただくが、この図の中の写像は点列を番号の順に写し、2次元の「安定多様体」と「不安定多様体」はポアンカレ写像に対する2つの不変曲線(SとU)になる。不安定な周期運動は、正確に周期Tで繰り返すので、写像に対する不動点として現れる。曲線SとUはこの周期運動の安定および不安定多様体に属する。SとUは、単一の滑らかな曲線とは違い、2つの異なる曲線として断面上に現れ、ある特殊な軌道に対しては2つの曲線が交わることになる。点列はnが無限に大きくなるとき不動点に接近する。ホモクリニックな交点はSにもUにも属するので、それが1つあると、無限に多くホモクリニック点を生み出す。これがポアンカレの「2重漸近」である。ホモクリニック点列から1次のホモクリニック軌道が生じ(説明省略)、2次、3次、4次...のホモクリニック軌道が生成される。
安定多様体Sと不安定多様体Uの1つの交点から出発して、そのような無限個の族が構成され、これらの点は曲線をホモクリニック・タングル(絡み)という一種の網、格子のようなものに貼り付けてしまう。網のすべての糸はSまたはUに属する弧であり、これらの糸は未来において最終的に鞍点(図のp)の左か右を通過する軌道を分離する。相空間の有限の領域に無限の「分離」が詰め込まれた状態だ。この状況はどのように与えられた初期条件から出発した軌道であっても、その未来を予測することは現実的に不可能になる。このホモクリニック・タングルは、今日カオスと呼ばれる現象の、最初の数学的な出現だったのだ。

このカオスの存在にに気がついたポアンカレの驚きは、本書の次のような記述でうかがい知ることができる。
拡大

拡大

「三体問題がいかに複雑なものか、またこの問題を解くためには、われわれの既知のすべての知識とは異なった超越的な知識が、いかに必要であるかもわかってくる。」
「その複雑さは驚くべきもので、私自身もこの図形を引いてみせようとは思わない。三体問題の複雑さに、もっと一般には、一価の積分をもたず、ボーリン(Bohlin)の級数が収束しないような、すべての力学の問題の複雑さに、なにかの概念を与えてくれるもの、またはそれに適したものは、これ以上なにもない。」
なお、本書の補遺は第3巻を理解するのに必要な最低限のことを第1巻から抜粋したものだが、実際のところ第1巻の他の章や第2巻の記述を参照せよとしている箇所がいくつも見られ、論理的な整合性を大切にして読むのであれば第1巻と第2巻は必須である。
第1巻では第1種の周期解の研究と、一価正則な積分の不存在の証明、永年項に関すること、そしてリントシテットによる方法の記述と解説にあてられている。第2巻と第3巻は、ギルデンによる方法の議論と、安定性の問題、第2種周期解および漸近解、二重漸近解の研究が解説されている。
ポアンカレは本書を『天体力学の新しい方法』と名付けたが、取り上げている3体問題は実際の惑星の運動ではほぼあり得ず、数学的な研究であるとしているが、正三角形解と直線解を導いた3体問題のラグランジュ解がトロヤ群と呼ばれる小惑星群として発見され安定な正三角形解の存在が裏付けられた。また、一般に3体問題はニュートン力学であるが、近年研究されている天の川銀河の中心のブラックホールSgr A*を周回する恒星の群れなどは、一般相対性理論を使って解くべき多体問題だ。(動画の引用元のページ)3体問題や多体問題(N体問題)はもはや数学の世界だけの話ではない。

この日本語版が刊行されたのは1970年、先日「映画『ファースト・マン(2018)』」として紹介したアポロ11号の翌年、大阪万博や三島事件があった年である。ポアンカレ以降50年経った1960年代からカオスは数学的な発展を再開したのだが、ウィキペディアの「カオス理論」という記事によると「この複雑な軌道の概念は1975年、ジェイムズ・A・ヨークとリー・ティエンイエンによりカオスと呼ばれるようになった。」ということだそうである。本書巻末の「解説」ではポアンカレの微分方程式論やトポロジー分野への功績の記述がほとんどで、彼がカオスを最初に垣間見たことに言及していないのはそのためである。原書タイトルにはない「常微分方程式」を日本語版の主タイトルにしたのも同じ理由だと思われる。
3体問題の動画は見ていて飽きない。3つ紹介しておこう。
非周期的(カオス)で3次元の3体問題
解の初期値鋭敏性が確認できる動画。開始2分あたりから軌道が分岐する。
周期解ばかりを集めたもの。とても面白い。
3体問題の動画: YouTubeで検索
原書のフランス語版は、昨年新装版が発売されたばかりだ。アマゾンジャパンから買うことができる。
「Les Méthodes Nouvelles de la Mécanique Céleste, Vol. 1: Henri Poincaré」(1892)
「Les Méthodes Nouvelles de la Mécanique Céleste, Vol. 2: Henri Poincaré」(1893)
「Les Méthodes Nouvelles de la Mécanique Céleste, Vol. 3: Henri Poincaré」(1899)



このフランス語版は3冊とも無料で公開されている。オンライン、PDFのほか各種フォーマットで閲覧できる。
オンライン閲覧:第1巻、第2巻、第3巻
セピア色のPDF: 第1巻、第2巻、第3巻
白黒のPDF: 第1巻、第2巻、第3巻
もちろん英語版も刊行されているが、高過ぎてお勧めできない。: Amazonで検索
より実用的な『天体力学講義(Leçons de Mécanique Céleste)』のフランス語版も新装版として昨年刊行されている。アマゾンジャパンから買うことができる。1912年に亡くなったポアンカレ最晩年の著作だ。英語や日本語には翻訳されていない。
「Leçons de Mécanique Céleste, Vol. 1: Henri Poincaré」(1905)
「Leçons de Mécanique Céleste, Vol. 2: Henri Poincaré」(1907, 1908)
「Leçons de Mécanique Céleste, Vol. 3: Henri Poincaré」(1910)



このフランス語版も無料で公開されている。オンライン、PDFのほか各種フォーマットで閲覧できる。
オンライン閲覧:第1巻、第2巻、第3巻
セピア色のPDF: 第1巻、第2巻、第3巻
白黒のPDF: 第1巻、第2巻、第3巻
今回の記事の続きは「ポアンカレによるカオスの発見と先見性」として補足している。合わせてお読みいただきたい。
関連記事:
ポアンカレによるカオスの発見と先見性
https://blog.goo.ne.jp/ktonegaw/e/daf1e56d0751c928592e75282d69835e
天体力学のパイオニアたち 上: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/5c51d50e2141c8ae58c9323ad49b65a1
天体力学のパイオニアたち 下: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/88846fbb12ed1f8b11a49f0659b93c75
数理解析のパイオニアたち: V.I.アーノルド
https://blog.goo.ne.jp/ktonegaw/e/165c894d023b1174fd519522935cdeeb
Hirsch・Smale・Devaney 力学系入門 ―微分方程式からカオスまで― 第3版
https://blog.goo.ne.jp/ktonegaw/e/98d451af90b7efc63aacbe4efdb330fa
力学系カオス: 松葉育雄
https://blog.goo.ne.jp/ktonegaw/e/12392ac282d10deed28914d8182c2286
古典力学の形成―ニュートンからラグランジュへ:山本義隆
https://blog.goo.ne.jp/ktonegaw/e/e808487b7e9d668967f703396e32d80a
全5巻完結!:ラプラスの天体力学論(日本語版)
https://blog.goo.ne.jp/ktonegaw/e/a720b0cfb775d00625763f87a56b2414
発売情報: 惑星探査機の軌道計算入門: 半揚稔雄
https://blog.goo.ne.jp/ktonegaw/e/a3aba0b87bff8a8ae54fb37ad1b04504


「ポアンカレ 常微分方程式 -天体力学の新しい方法-」

第22章:積分不変式
- 定常状態にある流体の運動
- 積分不変式の定義
- 不変式と積分の関係
- 相対不変式
- 不変式と偏差方程式の関係
- 不変式の変換
- 不変式と積分との間の他の関係
- 変数変換
- 諸注意
第23章:積分不変式の形成
- 積分因子の用法
- 力学の方程式
- 積分不変式と特性指数
- ケプラー変数の用法
- n°256の不変式に関する注意
- 縮減三体問題の場合
第24章:積分不変式の用法
- 検算法
- ヤコビの定理との関係
- 二体問題への応用
- 漸近解への応用
第25章:積分不変式と漸近解
- ボーリンの方法(再)
- 積分不変式との関係
- 別の論法
- 2次型不変式
- 制限問題の場合
第26章:ポアソン安定
- 安定性の諸定義
- 液体の運動
- 確率
- 諸結果の拡張
- 制限問題への拡張
- 三体問題への応用
第27章:後継点の理論
- 後継点の理論
- 不変曲線
- 諸結果の拡張
- 力学の方程式への応用
- 制限問題への応用
第28章:第二種周期解
- 第二種周期解
- 時間が陽に現われない場合
- 力学の方程式への応用
- 力学の方程式の第二種解
- 極大に関する諸定理
- 第二種解の存在
- 注意
- 特別の場合
第29章:最小作用原理の諸形式
- 最小作用原理の諸形式
- 運動学的焦点
- モーペルチュイ焦点
- 周期解への応用
- 安定解の場合
- 不安定解
第30章:第二種解の作り方
- 第二種解の作り方
- 解の効果的な作り方
- ディスカッション
- 特別な場合のディスカッション
- n°13の方程式への応用
第31章:第二種周期解の性質
- 第二周期解と最小作用の原理
- 安定と不安定
- ダーウィン軌道への応用
第32章:第二部類の周期解
- 第二部類の周期解
第33章:二重漸近解
- 種々の幾何学的表現法
- ホモクリーヌな解
- ヘテロクリーヌな解
- n°225(第2巻)との比較
- ヘテロクリーヌな解の例
補遺
1.ケプラー運動
2.制限三体問題
3.ケプラー変数の用法
4.一般三体問題
5.力学の一般的な問題
解説
1.Henri Poincaré について
2.常微分方程式論について
3.三体問題と常微分方程式論
年表






















すごい力作のブログですね。力学系、カオス好きで卒論で若干絡んでいたみとしてはとても興味をそそられます。
ポアンカレは、科学哲学の教科書として「科学と方法」他3部作で勉強したりオプション理論の元祖ともいえるバシェリエの先生だったり、数学以外でもとてもなじみがある大天才なので、とても楽しくブログを読ませていただきました。頑張ってそのうち読みたいと思います^^。
コメントありがとう。今週はウォーキングをサボってこの本を読んでいました。
卒論でも絡んでいたのですね。よしさんが専門の金融系の「相場の変動」は確率微分方程式が基礎だと思いますが、相場の振る舞いが時折見せる急激な変化はカオス的なものを感じさせますね。力学ではないけれど相場は多体問題です。
第1巻、第2巻や『天体力学講義(Leçons de Mécanique Céleste)』も原書で読んでみたいと思うようになりました。(それより「科学と方法」他3部作のほうが先かな?)
僕は絵的イメージで理解するタイプで分かりやすい説明図も得意なので、図の苦手な直感派って想像できない。
いろんな直感があるだろうとは思っていたけど。
僕も驚きました。絵的イメージはできたのかもしれませんが、描く能力が欠如していたのでしょう。そのような彼がトポロジーというモノのつながり方の研究者だったことも興味深いです。
「図画の試験で0点」の逸話は「天体力学のパイオニアたち 上: F.ディアク、R.ホームズ」のほうに書かれていました。
この解法は、さまざまなカオス分野でも応用されているのでしょうか?
また、100年以上前の原作・翻訳が今でも読まれているのも凄いことだと思いますが、この解法に関して近年の新しい著作や編集物はないのでしょうか?
的外れな質問かも知れませんが、アドバイス下されば幸いです。
こんにちは。コメントありがとうございます。
> この解法は、さまざまなカオス分野でも応用されているのでしょうか?
はい、カオス理論のその後の発展の基礎づけがこの本に書かれている数学的手法です。
その後の発展については次の本の第2章と第3章に書かれています。
天体力学のパイオニアたち 上: F.ディアク、R.ホームズ
また微分方程式の解の研究もポアンカレの業績です。その後の発展は次の本の第4章に書かれています。
天体力学のパイオニアたち 下: F.ディアク、R.ホームズ
上下巻とも、すでに紹介記事を書いていますので、よろしければお読みください。
> この解法に関して近年の新しい著作や編集物はないのでしょうか?
残念ながら日本語書籍では見つかりませんでした。「力学系カオス:松葉育雄」や「Hirsch・Smale・Devaney 力学系入門 ―微分方程式からカオスまで― 第3版」をお読みなるとその後の発展も含めて学べます。
一般向けの本では「カオス的世界像―非定形の理論から複雑系の科学へ:イアン・スチュアート」や「カオスとフラクタル (ちくま学芸庫):山口 昌哉」あたりがお勧めです。
「カオス的世界像―非定形の理論から複雑系の科学へ」と「カオスとフラクタル (ちくま学芸庫)」は読んだことがありました。
この先のポアンカレ解法を読みたいのですが、次のステップはなかなか敷居が高そうです。(値段も高そう)
一般向けと専門分野向けの中間ぐらいのレベルがよいのですが、そんな都合のよい書はなさそうですね。それでもいつかチャレンジしたいです。
両方ともお読みでしたか。(僕は未読ですので、読みたいと思っています。)
ポアンカレの解法は、常微分方程式の求積による解法、つまり大学1、2年で学ぶ解法をマスターしていることが前提ですから、一般向けと専門分野向けの中間ぐらいのレベルというのはなさそうですね。それにポアンカレの時代にはコンピュータがなく、それでも三体問題を解かなければという情熱で、ごりごり計算していたわけですから、コンピュータであっという間に計算できる今の時代には必要ないと思われます。ただし、学問的な興味としてはあり得ますね。
強いてあげれば(学部の3、4年レベルですが)次のような本があります。これもいずれ読んでみたいと思います。
常微分方程式:坂井秀隆
https://www.amazon.co.jp/&tonejiten-22/dp/4130629603