分子軌道法： 物理学と化学の境界

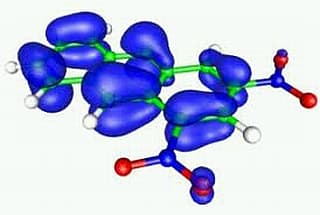
芳香族分子の構造と電子分布

「よくわかる量子力学：前野昌弘」という記事で書いたように、量子力学の教科書では３次元空間におけるシュレディンガーの波動方程式を極座標形式に変換してから「水素原子の電子雲（電子軌道）」といういちばん単純なケースで解を計算し、その後は多粒子系や場の量子化などの話に進んでしまう。

水素原子の電子雲（電子軌道）：画像クリックでJavaアプレットが開く。



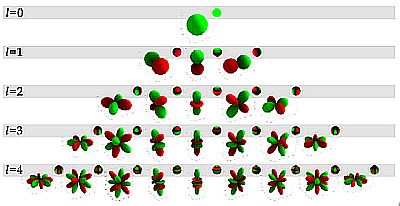
それでは水素原子よりも複雑な原子、分子のときはどうやって計算すればいいのだろう？水素原子でさえ計算はこんなに複雑なのだから、きっとものすごく難しいに違いないが計算の複雑さが増すだけなのだろうか？

このような疑問を解決してくれるのが「分子軌道法」だ。

分子の立体的な構造は電子の分布（軌道）によって決まってくるし、分子の構造や最外殻電子の分布は化学結合のしかたを決定する。スパコンを使ったマッチングの計算で抗癌剤など新薬が研究開発されるが、これは分子構造がわかってはじめて実現するものだ。分子軌道法は量子化学という分野の中核をなし、物理学と化学の境界に位置している。量子力学の応用例であり、化学反応の原理の出発点である。

今ではこの動画のように簡単に分子軌道を計算し、視覚化することできる。Winmostarはパソコンで動作するフリーウェアなのだ。



Winmostar（フリーウェア）のページ
http://winmostar.com/


水素原子だけでは飽き足らず、もっと複雑な原子、分子の電子軌道の計算方法を知りたい方のために、教科書を２つお勧めしておこう。どちらも森永茂先生がお書きになったもので入門書と専門書である。


「入門分子軌道法：藤永茂」（1990年刊行）、200ページ


ミクロの世界の法則－量子力学に基づく分子軌道法とはどのようなものかを、豊富な図表を用いて解説し、その発展する姿と分子計算の基本的考え方を示す入門書。量子力学の苦手な化学者や学部学生には好適の書。

難易度：「よくわかる量子力学：前野昌弘」が理解できた方ならば読めると思う。

第１章：電子と化学者
第２章：量子力学事始め
第３章：1中心1電子系
第４章：1中心2電子系
第５章：Pauliの原理
第６章：多電子原子
第７章：2中心1電子系
第８章：水素分子H2
第９章：等核2原子分子
第１０章：異核2原子分子
第１１章：多原子分子
第１２章：定性的MO法
第１３章：化学を計算で


「分子軌道法：藤永茂」（1980年刊行、2011年復刊）、430ページ


量子化学計算の基礎となる分子軌道法の専門書で、一度絶版を経て復刊した名著。
比較的古い本でもあるにもかかわらず、化学計算を専門にする人の多くに読まれているほど、内容は濃く使える。著者は物理学科出身でもあり、現在分子物理学などの発展もあることから、分子軌道法の知識は化学の分野に限定されず、物理学の分野の方にも多く必要とされている。
Hatree-Fock理論を中心に内容が展開されているが、群論が始めの章に表れてきたりと、非常に高度な内容となっているが、化学計算をする人は是非手にいれておくべき本である。

難易度：「現代の量子力学<上><下>：J.J.サクライ」や「量子力学 I、II：猪木慶治、川合光」など中級レベルの量子力学の教科書を理解できた方ならば読めると思う。

第１章：基礎方程式
第２章：変分法
第３章：分子の対称性と群論
第４章：ハミルトニアンと波動関数
第５章：Hartree-Fockの方法I
第６章：Hartree-Fockの方法II
第７章：軌道関数の実際的計算法
第８章：原子の電子構造
第９章：簡単な分子の電子構造 - ２原子分子
第１０章：簡単な分子の電子構造 - 多原子分子
第１１章：Hartree-Fock-Roothaan SCF法の簡単化
第１２章：Huckel近似の分子軌道法
第１３章：分子の形と反応
第１４章：Hartree-Fock近似をこえて
第１５章：今後の展望


著者：藤永茂先生の略歴
1948年　九州大学理学部卒業
現在　アルバータ大学化学教室教授
　　　（Professor、Department of Chemistry、Faculty of Science、University of Alberta、Canada）
主要著書　アメリカ・インディアン悲史（朝日新聞社）、分子軌道法（岩波書店）など

藤永茂先生のブログ：
https://blog.goo.ne.jp/goo1818sigeru


余談：来月末にNintendo 3DS LLが18,900円で発売されるそうだが、「世界で一番美しい元素図鑑：セオドア・グレイ」のような図鑑の素材が3Dで撮りなおされ、立体元素図鑑や3D分子モデリングもできる立体分子図鑑が3DS、3DS LLのソフトになればいいのにと思った。きっと売れると思う。


応援クリックをお願いします！このブログのランキングはこれらのサイトで確認できます。
　　




関連ページ：

分子軌道法
http://akrmys.com/InCh2001/sect6.html

第４章：分子軌道法（裳華房）のサンプルページ（PDF)
http://www.shokabo.co.jp/sample/3225s.pdf

混成軌道と多重結合、分子軌道法（PDF）
http://www.ml.seikei.ac.jp/tsubomura/education/muki1/muki1-5.pdf