おみやげ算の続きです。
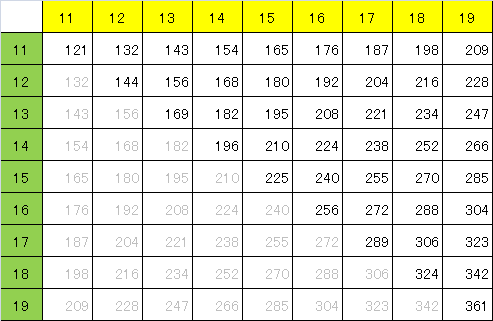
インドの子どものように、19x19までを暗記しようかと思い、表にしました。
これを、家のあちこちに貼ったり、手帳に挟んだりして、いつも見ていれば覚えられるような気がします。
17の二乗=289 この289の数字。
2でも3でも4でも割れないなあと考えているうち、17でしか割れないことに気づいた。
そこで、wikipediaで見ると、いろんな事が書いてある。
●289は、90番目の半素数である。
素数というのは、約数が1と自分自身のみの数字。つまり、3は素数、4は2で割れるので素数ではない。
半素数とは?半素数とは、2つの素数の積で表わされる自然数とのことだそうだ。知らなかった。
つまり、4(2x2)、6(2x3)、9(3x3)、10(2X5)、14(2x7)・・・・・・287(41x7)、289(17x17)、291(97x3)・・・・
●289は9番目のフリードマン数。
フリードマン数というのは、その数に使われている数字を全て用いて数式を作って元の数に一致させることができる数のこと。
289=(8+9)の2乗 2と8と9を使って、289を表せることができるということだ。
他には、153=51x3 とか 126=21x6とか 1255=251X5とか。
凄く面白い。
数学専攻の学生って、こんなことを習っているんだろうか。


























教えていただいてありがとう。
う~ん、覚えられるかなぁ、45だからいけるかな。
孫が2年生になるから、かけ算が始まります。
ばあちゃんも頭の体操と思ってチャレンジするかな?
11×13の欄、隣と同じ数字になってますよ。
間違いを教えていただいて、ありがとうございます。
エクセルの計算式を間違えてしまって・・・
お孫ちゃんと一緒にやると、いいですよね。
ぜひぜひ、お孫ちゃんにも九九から19x19まで、
挑戦して欲しいです。
それから、セミダブルについても、また教えて下さい。
どの部分をもって、セミダブルというのかが、よくわからないのです。
深く見ていなっかた、いろんな専門用語あるのね
半素数、フリードマンとか奥が深いんですね
認知症の防止によいかも・・・あまり近寄りたくない
また投稿しまーす
確かに、今となっては…という気がしないでもないですが、
「わぁー、面白い」と感じられるのもいいかなとも思います。
みたいな式で横にオートフィル
そのまま縦にオートフィルで式をコピー
一つの式だけでできますよね。
まったくの老婆心ですが...。(^^ゞ
おっしゃるとおりです。
今、試してみました。
何べんも、教えてもらいましたよね。
Excel基礎編とか中級編とか、、、
あの頃は楽しかったなあと懐かしいです。
ますたあさんは、過去を懐かしむより、常に前進あるのみでしょうか。
過去を懐かしんだり、あの時はとか思うこともありますが
基本的に、超ポジティブシンキングですね。
この先にきっと面白いことが待ってるとか
良い局面に巡り合えるとか。
でも、自分で打開していくって感じかな~。
それと、年を取ったのであまり細かいことを
気にしなくなりました。