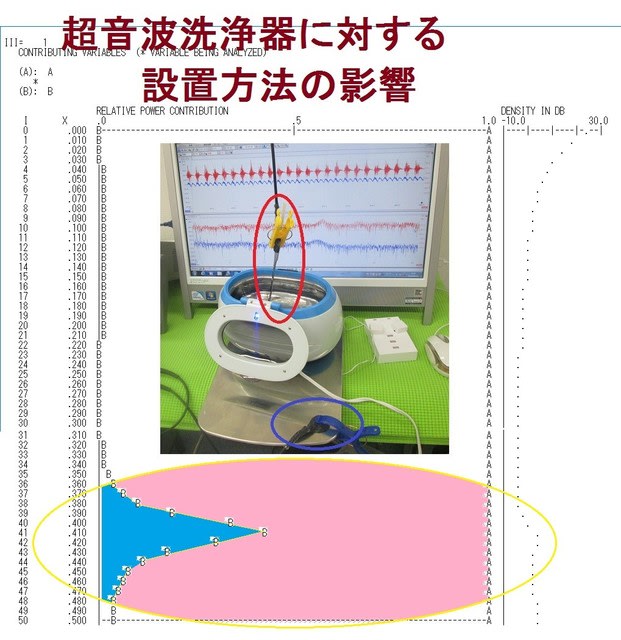
超音波発振による相互作用を考慮した「超音波制御技術」
変化する要因とともに
水槽が、大きく変化している場合があります
この場合の制御は難しく
対応すればするほど様々な状態になります
やはりしっかりした水槽を利用することが大切です
水槽が決まっている場合は
水槽に合わせた利用を考える必要があります
参考写真を紹介します
赤池弘次会員の京都賞受賞に寄せて
北川 源四郎 http://wwwsoc.nii.ac.jp/msj6/sugakutu/1103/kitagawa.pdf より
現役時代の赤池氏は，
私たちに統計科学の研究者は人の3 倍勉強しなければならないと説いていた．
数理的な研究，
応用対象領域の研究
そしてデータ解析・計算法の研究である．
純粋数学に徹するならばともかく，応用を目指すからには，その覚悟が必要であり，それを成し遂げた先に，次世代を牽引する新しい科学的方法が見えてくることを，赤池氏の成功は物語っているように思える．これは統計科学に限らず，広く数理科学の研究者が心すべきことであろう．
現役時代の赤池氏は，
私たちに統計科学の研究者は人の3 倍勉強しなければならないと説いていた．
数理的な研究，
応用対象領域の研究
そしてデータ解析・計算法の研究である．
純粋数学に徹するならばともかく，応用を目指すからには，その覚悟が必要であり，それを成し遂げた先に，次世代を牽引する新しい科学的方法が見えてくることを，赤池氏の成功は物語っているように思える．これは統計科学に限らず，広く数理科学の研究者が心すべきことであろう．
＜超音波のダイナミックシステム＞ Ultrasonic-Laboratory
超音波水槽内の液循環を
システムとしてとらえ、解析と制御を行う
多くの超音波（水槽）利用の目的は、
水槽内の液体の音圧変化の予測
あるいは制御にあります。
しかし、多くの実施例で
理論と実際の違いによる問題が
多数指摘されています。
この様な事例に対して
１）障害を除去するものは
統計的データの解析方法の利用である
＜超音波伝搬状態の計測・解析技術＞
２）対象に関するデータの解析の結果に基づいて
対象の特性を確認する
＜洗浄対象物、攪拌対象物、治工具・・・の
音響特性を検出する技術＞
３）特性の確認により
制御の実現に進む
＜キャビテーションのコントロール技術＞
といった方法により
超音波を効率的な利用状態に改善し
目的とする超音波の利用を実現した
液循環効果の利用例が多数あります
参考
ダイナミックシステムの統計的解析と制御
：赤池弘次/共著 中川東一郎/共著：サイエンス社
超音波システム研究に関する動画 ultrasonic-labo
音と超音波の組み合わせを利用した超音波制御技術 ultrasonic-labo
超音波の発振制御技術
超音波システム研究所は、
シャノンのジャグリング定理を応用した「超音波制御」方法について
超音波データのバイスペクトル解析による、
超音波伝搬現象に関する分類方法に基づいた
制御設定を行う方法を開発しました
この技術を、コンサルティング提案・実施対応しています。
超音波伝搬現象を、安定して効率よく利用するためには
超音波の伝搬特性として、発振機や振動子以外の条件に関する
応答特性・相互作用の検討や
専用治工具の開発も必要です
発振波形や制御条件を検討することで
新しい超音波の効果（注１：オリジナル非線形共振現象）を発見できます
非線形現象を主要因とした、超音波現象を目的に合わせて利用することで
効率の高い超音波利用が実現します
特に、ナノレベルの超音波技術での実績が増えています
注１：オリジナル非線形共振現象
オリジナル発振制御により発生する高調波の発生を
共振現象により高い振幅に実現させたことで起こる
超音波振動の共振現象
＜制御について＞
各種データの時系列変化の様子を解析・評価して、
時間で移動するボールのジャグリング状態に相当する
超音波伝搬現象の「サイクル」と、「影響範囲」について
超音波の分類から
線形型、非線形型、ミックス型、変動型として
論理モデルを構成します
この論理モデルからボールＮ個のジャグリング状態を設定して制御を行い、
音圧測定解析により、モデルの調整を行うと、
システムの状態に適した制御が実現し、
効率の高い超音波システムとなります
＜＜ シャノンのジャグリング定理の応用 ＞＞
注：JUGGLING THEOREM proposed by Claude E. Shannon
シャノンのジャグリング定理
( F + D ) ＊ H = ( V + D ) ＊ N
F ： ボールの滞空時間（Flight time）
D ： 手中にある時間（Dwelling time）
H ： 手の数（Hands）
V ： 手が空っぽの時間（Vacant time）
N ： ボールの数（Number of balls）
＜＜ 応用 ＞＞
F ： 超音波１の発振制御
D ： ベースとなる超音波２の発振制御
H ： 基本サイクル
（音圧データの解析結果：バイスペクトルを数値化したパラメータ）
V ： 振動（固有振動・・）装置・・の運転制御
N ： 超音波（発振）機器の数
ポイント（ノウハウ）は、非線形現象の発生状態を
対象物による相互作用を考慮した
測定解析評価に基づいて、コントロールすることです。
