超音波による<表面改質>技術
ものの表面を伝搬する弾性波に関しての
実験・検討を行っています
<<超音波システム研究所>>
ものの表面を伝搬する弾性波に関しての
実験・検討を行っています
<<超音波システム研究所>>
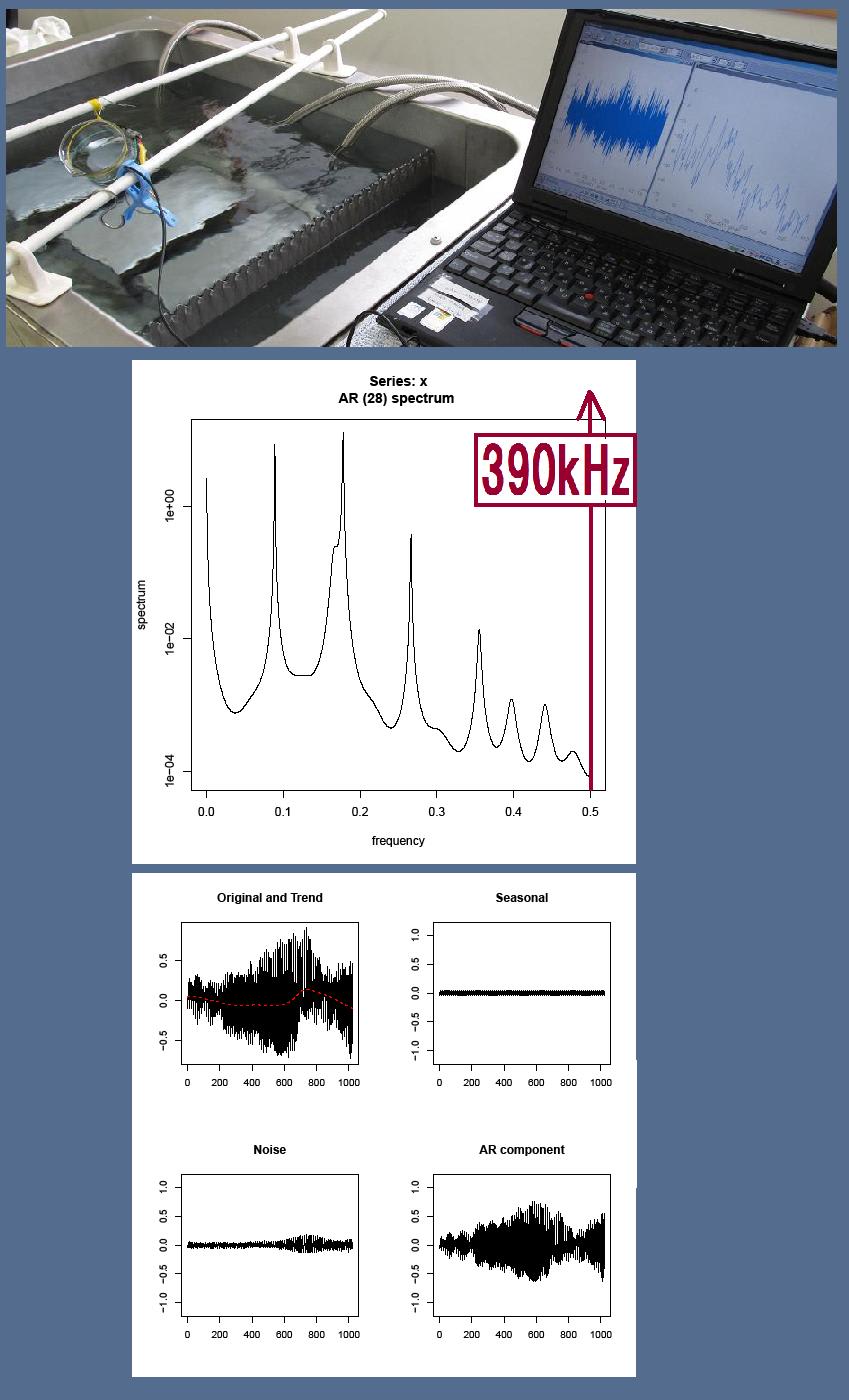
超音波振動子を利用した振動測定no.20
超音波振動子を利用した振動測定
超音波振動子を利用した測定
超音波計測システムの実験外観です。
測定データを解析することで状態の特徴を検出します。
< 超音波システム研究所 >
湯川秀樹 「創造への飛躍」より
...かくして得られた結論は、
「これほどの研究があるからには
東洋人でもこれに専念すれば
終に欧米に遜色なきに至らんと
確信を得るに至りました。
これが私をして物理学に
執着するに至らしめた根源であります」
長岡先生の出発点が、このようであったればこそ、
果たして明治三十七年(一九〇四年)には
世界の物理学者に先駆けて
原子模型に関する論文を発表するに至ったのである。
今にして思えば、
このような大先輩を日本人の中に見出していたことが、
大正末期の高校生であった私をして、迷うことなく、
物理学研究の道を選ばしめる要因の一つとして
大きく作用していたのではなかろうか。
学問は勝負事ではない。
しかし、やはり気合が大切である。
学問は芸術とも違う。
しかし、気塊が肝要なことに変わりは無い。
要するに学問することそれ自身が執念です。
コメント
物事を深め、探求していくときには
「執念・気合」といったものが
その人間に意識されていることを考えさせられます
もっと、もっと、「執念・気合」の追及が必要な気がします
超音波振動子を利用した振動測定
超音波振動子を利用した測定
超音波計測システムの実験外観です。
測定データを解析することで状態の特徴を検出します。
< 超音波システム研究所 >
湯川秀樹 「創造への飛躍」より
...かくして得られた結論は、
「これほどの研究があるからには
東洋人でもこれに専念すれば
終に欧米に遜色なきに至らんと
確信を得るに至りました。
これが私をして物理学に
執着するに至らしめた根源であります」
長岡先生の出発点が、このようであったればこそ、
果たして明治三十七年(一九〇四年)には
世界の物理学者に先駆けて
原子模型に関する論文を発表するに至ったのである。
今にして思えば、
このような大先輩を日本人の中に見出していたことが、
大正末期の高校生であった私をして、迷うことなく、
物理学研究の道を選ばしめる要因の一つとして
大きく作用していたのではなかろうか。
学問は勝負事ではない。
しかし、やはり気合が大切である。
学問は芸術とも違う。
しかし、気塊が肝要なことに変わりは無い。
要するに学問することそれ自身が執念です。
コメント
物事を深め、探求していくときには
「執念・気合」といったものが
その人間に意識されていることを考えさせられます
もっと、もっと、「執念・気合」の追及が必要な気がします
<<超音波測定技術>>No.5
超音波測定技術
オシロスコープに圧電素子を接続しています
オシロスコープの電圧変化をモニターで観察しています
データの解析
(自己回帰モデルによるフィードバック解析)により、
特徴を検出します
超音波測定技術
オシロスコープに圧電素子を接続しています
オシロスコープの電圧変化をモニターで観察しています
データの解析
(自己回帰モデルによるフィードバック解析)により、
特徴を検出します
超音波計測制御技術no.18
新しい超音波計測システムの測定状態です。
測定データを弾性波動を考慮した解析で、
各種振動状態の特徴を検出します。
< 超音波システム研究所 >
新しい超音波計測システムの測定状態です。
測定データを弾性波動を考慮した解析で、
各種振動状態の特徴を検出します。
< 超音波システム研究所 >
超音波測定技術NO.41
複雑に変化する超音波の利用状態を、
音圧や周波数だけで評価しないで
「音色」を考慮するために、
時系列データの自己回帰モデルにより解析して
評価・応用しています
<<超音波システム研究所>>
複雑に変化する超音波の利用状態を、
音圧や周波数だけで評価しないで
「音色」を考慮するために、
時系列データの自己回帰モデルにより解析して
評価・応用しています
<<超音波システム研究所>>
超音波照射実験 no.19
Ultrasonic Cavitation Control.
超音波の非線形性現象を利用しています。
Ultrasonic Sound Flow water effect.
<<超音波システム研究所>>
Ultrasonic Cavitation Control.
超音波の非線形性現象を利用しています。
Ultrasonic Sound Flow water effect.
<<超音波システム研究所>>
超音波計測技術no.33
超音波計測技術
(振動子 1.6MHz 、2.5MHzを利用した振動計測)
新しい超音波計測システムの測定状態です。
測定データを弾性波動を考慮した解析で、
各種の振動状態を検出します。
< 超音波システム研究所 >
関係各位
2011年4月24日
超音波システム研究所
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
超音波測定・解析システム no.2
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
超音波システム研究所は、
以下の通り、展示会に出展します。
2011年6月29日(水)~7月1日(金)
第24回 インターフェックス ジャパン
会場:東京ビッグサイト
主催:リード エグジビション ジャパン株式会社
**出展概要**
http://ipj2011.tems-tem.com/exhiSearch/IPJ/jp/searchResult_detail1.aspx?id=61bc5bcf-ee63-4763-adbe-cd2e12fac659
超音波測定・解析システム
2009.10.1より販売中の
「測定システム」を改良しました
解析システムを追加して
2011.6.1より販売します
振動子 1.6MHz 、2.5MHzを利用した振動計測
新しい超音波計測システムの測定です。
測定したデータについて、弾性波動を考慮した解析で、
各種の振動状態(モード)として検出します。
複雑に変化する超音波の利用状態を、
音圧や周波数だけで評価しないで
「音色」を考慮するために、
時系列データの自己回帰モデルにより解析して
評価・応用しています
目的に応じた利用方法が可能です
例1:超音波水槽内の音圧管理
例2:超音波洗浄機の超音波周波数の確認
例3:洗浄対象物(材質、数量、治工具・・)
による超音波の伝搬状態の確認
例4:超音波攪拌における超音波条件の設定
・・・・・・・・・
http://youtu.be/BCPtjxBJT2s
http://youtu.be/shwI_gkPtVA
http://youtu.be/cOXo-R8pggs
http://youtu.be/aqKifmWGmE0
http://youtu.be/prrpId1vTBU
http://youtu.be/2SL5SkZoPzs
ご希望の方はメールでお問い合わせください
超音波システム研究所
URL:http://www.green.dti.ne.jp/aabccdx/
超音波計測技術
(振動子 1.6MHz 、2.5MHzを利用した振動計測)
新しい超音波計測システムの測定状態です。
測定データを弾性波動を考慮した解析で、
各種の振動状態を検出します。
< 超音波システム研究所 >
関係各位
2011年4月24日
超音波システム研究所
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
超音波測定・解析システム no.2
━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━
超音波システム研究所は、
以下の通り、展示会に出展します。
2011年6月29日(水)~7月1日(金)
第24回 インターフェックス ジャパン
会場:東京ビッグサイト
主催:リード エグジビション ジャパン株式会社
**出展概要**
http://ipj2011.tems-tem.com/exhiSearch/IPJ/jp/searchResult_detail1.aspx?id=61bc5bcf-ee63-4763-adbe-cd2e12fac659
超音波測定・解析システム
2009.10.1より販売中の
「測定システム」を改良しました
解析システムを追加して
2011.6.1より販売します
振動子 1.6MHz 、2.5MHzを利用した振動計測
新しい超音波計測システムの測定です。
測定したデータについて、弾性波動を考慮した解析で、
各種の振動状態(モード)として検出します。
複雑に変化する超音波の利用状態を、
音圧や周波数だけで評価しないで
「音色」を考慮するために、
時系列データの自己回帰モデルにより解析して
評価・応用しています
目的に応じた利用方法が可能です
例1:超音波水槽内の音圧管理
例2:超音波洗浄機の超音波周波数の確認
例3:洗浄対象物(材質、数量、治工具・・)
による超音波の伝搬状態の確認
例4:超音波攪拌における超音波条件の設定
・・・・・・・・・
http://youtu.be/BCPtjxBJT2s
http://youtu.be/shwI_gkPtVA
http://youtu.be/cOXo-R8pggs
http://youtu.be/aqKifmWGmE0
http://youtu.be/prrpId1vTBU
http://youtu.be/2SL5SkZoPzs
ご希望の方はメールでお問い合わせください
超音波システム研究所
URL:http://www.green.dti.ne.jp/aabccdx/
超音波測定技術
超音波の周波数について
超音波の周波数について
各種の構造や反応に対して、適切な周波数があります
的確に検討するためには、沢山の周波数が必要ですが
現状では出来ません
電圧素子の量産からくる制限が大きな理由ですが
周波数の違いは大変な違いを生み出します
5-20kHzの違いで
全く異なる結果になることも珍しくありません
周波数を効率的に考えるヒント
物事を波として捉えるために
参考
波として考えた時、
「空中に放たれたボールが放物線を描いて曲がる」
ような現象はどう考えればよいか?
1:古典力学的に考える
位置エネルギーの高い方から
低い方へ「力」が働くことで「落ちる」。
2:シュレーディンガー方程式から考える
位置エネルギーが大きいところでは
運動エネルギーが小さくなる。
つまり「高いところでは波長が長くなる」
従って、波が進むと、「落ちる」方向へ曲がって行く。
コメント
どうしても、日常の物事は古典力学的に考える習慣が
身についてしまっているように感じますが
もっと(正確にと言う意味を含めて)
「重力で考えるのではなく」、
「物質の波長」で考える
ようにして、思考の新たな展開をすると、
水中の音波と洗浄対象物の
波長に関する問題や応用が見えてきます
補足
シュレディンガーの波動方程式は、
"物質波”という考えに基づいて構成されています。
その波動とは通常の波動ではなく、確率波です。
(規格化をして、
波動関数の絶対値の2乗が確率密度となる。
連続関数となる。発散しない。 等 )
そして、その自乗は粒子の確率分布を表し、量子はそのどこかに
“点”として存在していることになります。
以上により、シュレディンガーの波動方程式は確率微分方程式です。
確率微分方程式を解くことは難しいのですが、
(伊藤型として書き下すことで)
伊藤の公式により解けるようになっています
この公式は、
デリバティブ、
殊にオプション金融商品の開発・普及・改良に必要不可欠な、
大変に重要な公式です。
Excelを利用して簡単に解くことが出来ます。
ここで私が補足したかったことは、
量子力学と金融商品が
確率微分方程式でつながっているように、
量子力学と超音波が
波動方程式でつながっているので
積極的に量子力学や金融工学に対しても関心を持ち、
微分方程式や考え方を
具体的・工学的に応用・利用していくことが大切だと言うことです
超音波の周波数について
超音波の周波数について
各種の構造や反応に対して、適切な周波数があります
的確に検討するためには、沢山の周波数が必要ですが
現状では出来ません
電圧素子の量産からくる制限が大きな理由ですが
周波数の違いは大変な違いを生み出します
5-20kHzの違いで
全く異なる結果になることも珍しくありません
周波数を効率的に考えるヒント
物事を波として捉えるために
参考
波として考えた時、
「空中に放たれたボールが放物線を描いて曲がる」
ような現象はどう考えればよいか?
1:古典力学的に考える
位置エネルギーの高い方から
低い方へ「力」が働くことで「落ちる」。
2:シュレーディンガー方程式から考える
位置エネルギーが大きいところでは
運動エネルギーが小さくなる。
つまり「高いところでは波長が長くなる」
従って、波が進むと、「落ちる」方向へ曲がって行く。
コメント
どうしても、日常の物事は古典力学的に考える習慣が
身についてしまっているように感じますが
もっと(正確にと言う意味を含めて)
「重力で考えるのではなく」、
「物質の波長」で考える
ようにして、思考の新たな展開をすると、
水中の音波と洗浄対象物の
波長に関する問題や応用が見えてきます
補足
シュレディンガーの波動方程式は、
"物質波”という考えに基づいて構成されています。
その波動とは通常の波動ではなく、確率波です。
(規格化をして、
波動関数の絶対値の2乗が確率密度となる。
連続関数となる。発散しない。 等 )
そして、その自乗は粒子の確率分布を表し、量子はそのどこかに
“点”として存在していることになります。
以上により、シュレディンガーの波動方程式は確率微分方程式です。
確率微分方程式を解くことは難しいのですが、
(伊藤型として書き下すことで)
伊藤の公式により解けるようになっています
この公式は、
デリバティブ、
殊にオプション金融商品の開発・普及・改良に必要不可欠な、
大変に重要な公式です。
Excelを利用して簡単に解くことが出来ます。
ここで私が補足したかったことは、
量子力学と金融商品が
確率微分方程式でつながっているように、
量子力学と超音波が
波動方程式でつながっているので
積極的に量子力学や金融工学に対しても関心を持ち、
微分方程式や考え方を
具体的・工学的に応用・利用していくことが大切だと言うことです