最近の小学生は速度を計算するのに「はじきの法則」なるものを使うらしい。
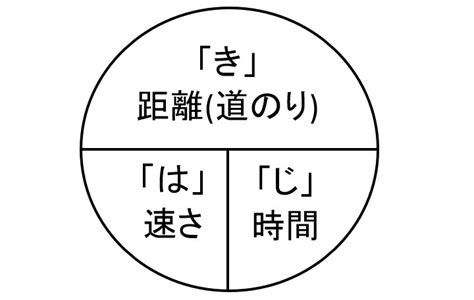
「速さ」と「時間」をかけると「距離」になり、「距離」を「速さ」で割ると「時間」になり、「距離」を「時間」割ると「速さ」になる、と。
なるほど。
中学生辺りになると、もうちょっとつや〜な書き方になるわけだな。

高校生くらいのレベルでもっとつや〜に表現するとこうなる。
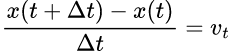
小学生で習う(らしい)「はじきの法則」と同じ事を表現してても随分と見た目は変わるもんだ(笑)。「移動距離」は、例えば地点Aを午前8:00に出発して地点Bに午前8:15に着いたとすると、地点Bの位置情報から地点Aの位置情報を引いたモノ、となる。
そして「かかった時間」は8:15 - 8:00なら15分、となってΔtは15分、って事になるよな。
ここで重要なのは「位置情報」ってのは「恐らく」時間の関数だろう、と「仮定」してる事だ。本当にそうなのか、は分からん。一応汎用性がある、って事でそういう前提になってて、唯一小学生の「はじきの法則」と違うトコがあるとすればその辺だ。
「地点Aから地点Bへの移動時間」が15分だとしても、途中でおっぱいが大きな女を見かけて立ち止まったり(笑)、あるいは小便したくて立ちションすっかもしんない。
いずれにせよ15分内で「常に同じ歩数で歩いてる」たぁ限らないんで、要は数理的には定数、つまり一定だとは限らないわけだ。「変動はあり得るよ」と言う前提だと位置情報は「時間の関数」だと「仮定」してた方がイイ、っつーわけだ。
さて、上の式をこう書き換える。
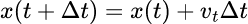
これは「B地点にいる」っつー事は「A地点にいる」と言う位置情報に速さと「移動にかかった時間」をかけたモノを足した、っつー事だ。それは数式の書き換えでそのまんまだろう。
しかし、ちょっと考えてみると、例えば地点Aに午前8:00にいて、地点Bに午前8:15にいたとする。これが「t」の情報なんだけど、「8時いらなくね?」とならないか(笑)?必要な情報は「どこにいたのか」と「何分かかったか」と言う事だけ、だ。
そこで次のように書き換えてみよう。
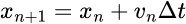
位置を計算するにはそれ以前に「いた」位置に速さと「移動にかかった時間」を掛けたものを足す・・・。まあ当たり前なんだけど、n + 1番目の「位置」を計算するにはn番目にいた「位置」が必要だ、って事だな。
実はこの変換で厄介な事が1つ出てくる。「速さ」が何を表すのかよく分からなくなってしまった・・・と言うのも「はじきの法則」から言うと移動距離をかかった時間で割ったものが「速さ」の定義だった筈なのに、ここではまるで別の量のように見えるから、だ。
しかしその辺は後回しにして目をつぶると、これは数学的には数列の問題に見える。そしてこの形式の問題を差分方程式と呼ぶ。
差分方程式、とはこれまた厳つい名称なんだけど、n + 1番目を計算するのにn番目の情報が必要・・・とくれば、これはプログラミング的には単に再帰の問題だ。そう、名称は厳つい差分方程式だけど、単に再帰の事を言ってる。「現時点いる位置を知る」のは再帰的な問題なんだ(※1)。
ここで僕らは既知の「プログラミングテクニック」の問題にすり替えられるわけだ。
でも困るのは「速さ」の問題だ。これは一体どうすればいいんだろう。「はじきの法則」をそのまま当てはめると全部の項が消えてしまう。これはマズい。
しかし、さっき、「おっぱいの大きい女を見て」振り返って「単位時間内の歩数」が減る可能性がある、と論じた。言い換えると「歩く速さ」も一定じゃない可能性がある・・・と言うか、僕らの日常を鑑みると、毎分何歩、って決まった速さで移動してるたぁ限らない。これも当然だよな。
って事は、「速さ」も時間の関数と「仮定」してもバチは当たらないんじゃないか、と言う話になる。
そこで、「はじきの法則」を真似して次のような数式をでっち上げる。
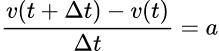
先程の「移動距離」の数式の変形も真似して次のように書き換えよう。
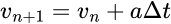
そうすると、これも形式的には先程と同じように差分方程式・・・つまり再帰になる。aが何なんだかサッパリ分からないが(笑)。
まぁ、ハッキリ言っちゃって、問題を先送りしただけ、なんだけど(笑)、実は差分方程式に変換する前のaの定義式(に見えるブツ)は中学校2年か3年の数学で習うトコの平均の傾きだ。もうちょっとカッコよく言うと平均変化率と言う。
つまり、速さは距離と時間に於いての平均変化率で、同様に、速さと時間に於いての平均変化率をaとしたわけだ。このaを一般に加速度と呼ぶ。
しかし、ここまで読んできた人は、
「距離は時間の関数と仮定したんでしょ?速さも時間の関数と仮定したんでしょ?加速度も時間の関数と仮定出来るんじゃない?つまり、問題は解決せずに先送りでしょ?」
と思うかもしんない。正しいわ(※2)。
でもここでは地球の地表から適当にボールを投げる「斜方投射」を扱う。この時出てくる加速度が重力加速度と呼ばれるもので、幸い、地表付近だと定数である事が知られている。その値は9.8m/s^2。
と言うわけで、今回、パソコン上で扱う重力加速度gは定数なんでここで打ち止め、だ。
めでたし、めでたし。安心して欲しい。
ところで、今までの議論で言うと、速度も加速度も中学校の数学で言う平均の傾き、とか平均変化率、と呼ばれるモノだった。
数学的に言うと、関数上の適当な二点間で定義される「傾き」なわけだな。
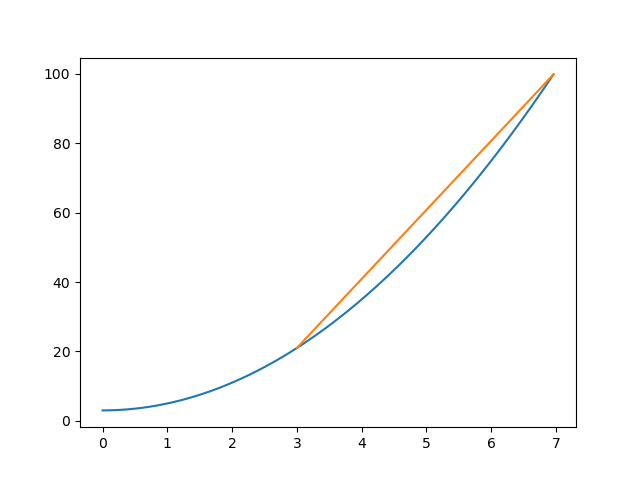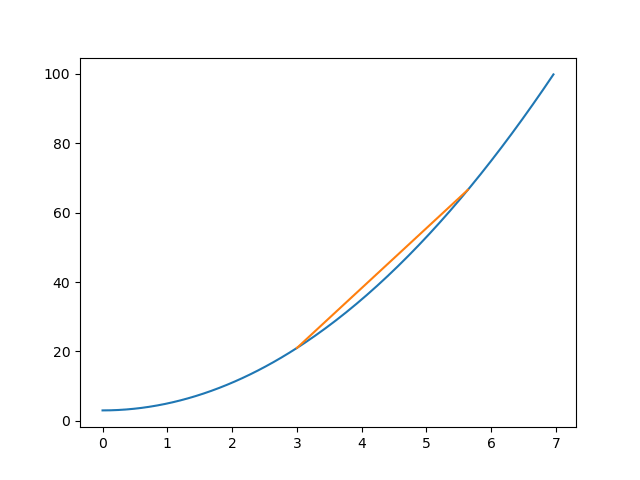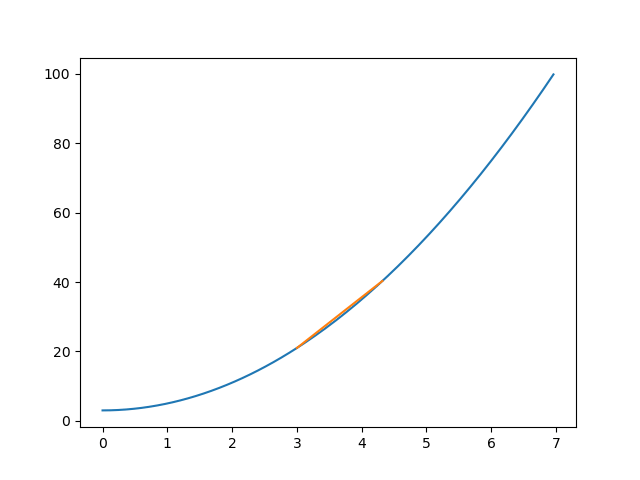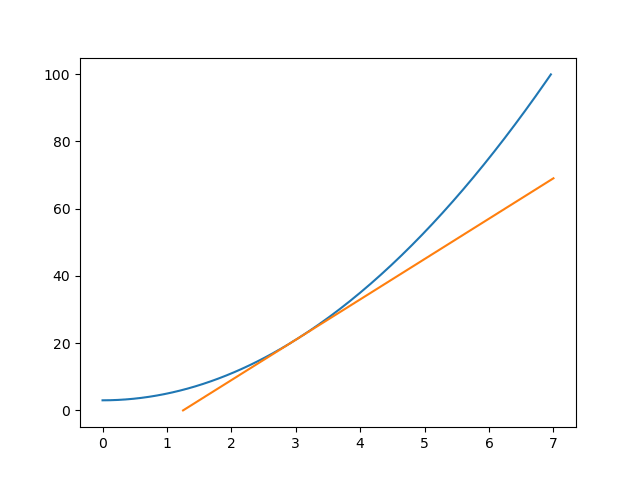
上のgifアニメを見て欲しいんだけど、仮に二点間の距離をどんどん縮めて行くと当然一点に行き着くんだけど、この時、「平均」変化率だったものが単なる「変化率」に変わる。具体的に言うと「平均の傾き」がその1点で接する直線(接線と呼ぶが)の「傾き」に一致する。
この議論で見ると、速度に関してもある地点からある地点に行く移動距離とそれにかかる「時間」が短くなれば「平均の速さ」はある時点での「速さ」に近づいていく。
この操作を微分と呼ぶわけだ。
ところが、上はgifアニメとして作ったが、要は「作画すると明らか」なんだけど、これを数学的に論じようとすると凄い厄介なんだよな。なんせ計算上は「平均変化率」の定義によりΔtは0となり、移動距離(そして速度の変化)を0で割る事になる。
現実的には「作図」は出来るのに、計算が破綻しちまうわけだ(※3)。
まぁ、微分の話はおいておく。その辺は数学者に任せりゃエエ話だ。
しかし、知っておいて欲しいのは、実は現実でもプログラミングでも平均の速さは得られても単なる速さは得られないと言う辺りだ(※4)。移動距離を算出するのに速さを利用する以上、ここは押さえておかないとならない。
ここでは斜方投射、と呼ばれる現象をアニメーションさせてみようと思ってるが、例えばボールをポーンと投げて、Δtを1時間とか取ってもあまり現実とそぐわない結果になるだろう、ってのはなんとなく分かる?
一方、Δtを一秒よりも小さく取っておけば、僕らの「現実世界を見る目」をなんとなく誤魔化せるだろうな、ってのも予想がつくと思う。そして小さい時間を利用して計算した「平均の速さ」を使って、細かくボールの挙動を追っていけばまぁまぁの完成度のアニメーションになるんじゃないか、と期待が持てる。
そしてそのための差分方程式なんだ。
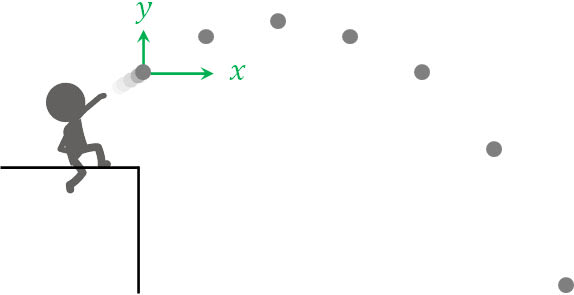
さて、「斜方投射」は二次元平面上での「運動」になる。必要なのは地表に対して垂直の位置情報yと並行な位置情報xの2つだ。
そして垂直軸yでは負の方向に重力加速度が生じる。一方、水平方向には何も加速度がない。
この「水平方向に加速度がない」運動を、中学校理科では「等速直線運動」と教える。現実には空気抵抗があったりするが、それが無い場合、水平にボールを投げた(つまり初速を与えた)場合、どこまでもその「最初の速さ」のままで突き進んでいく。それが理論的な「結果」だ。
一方、垂直方向は等速直線運動じゃない。これも広く知られているだろう。
もし、垂直方向が等速直線運動だったら僕らがジャンプすると、そのまま進んでいって宇宙の彼方まで「ジャンプした時と同じ速さで」突き進んでしまう。
言い換えると「死ぬ」(笑)。現実はそうじゃないんで、良かった、と言いたいトコだ(笑)。
ジャンプしても元の地点へ「落ちて」くるのは重力加速度の仕業だ。重力加速度は常に地球の中心に向かって働いてくれる。
さて、ここで初速v0、地表からの角度θでボールを投げる事をする。
これだけの情報でx軸方向の初速、y軸方向の初速が決まる。
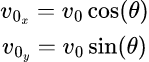
この時点で、「速さ」がx方向とy方向に分けられる。「速さ」は大きさだが、この時点で「方向」が出てくる。数学的には「ベクトル」と呼び、ベクトルになった「速さ」を「速度」と呼ぶ(※5)。
そして、前出の差分方程式を使って、x方向、y方向にそれぞれ式を設定しよう。
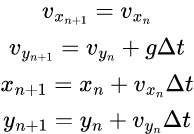
これで準備は整った。
もう一度繰り返すが、差分方程式とは再帰の事だ。
Lispなんかだと上記の式を見ただけで華麗にそのまま再帰を書き下したくなるだろう。
一方、この問題特有の問題点やPythonならではの問題がある。それはちょっと後で論じよう。
なお、通常上のような式を見たら、C言語脳ならループをしながら速さや位置情報を書き換える手段を取るだろう。
しかし、何度も言うけど、C言語のようにPythonを使うのは間違っている。PythonならPythonらしいコードを書くべきなんだよ。
そりゃそうだろ、C言語のように書きたければC言語を使えばいい話だ。わざわざPythonを使う必要はない。
よってここでは、C言語やPascal、Javaのような書き方はしない。そして最悪な事に、このテの数値計算アルゴリズム関連の書籍ではC言語やPascal、Javaのような「組み立て方」しか教えんのだ。
だからそれらの記述法は無視する。言っちゃえばC言語やPascal、Javaで書くようなダセェコードは書かない。
しかし、そう言うと、「数値計算のアルゴリズムは速度が必要で・・・」とか世迷い事を言う層が現れるかもしんない。こういうのも無視しとく。何故なら計算速度が本当に必要なら、Pythonを選択する事自体が間違ってるんだよ(笑)。C言語かFortranで書いとけ(笑)。わざわざ遅い言語を選択しといて「速度が〜」とか言うのは単なる戯言だ。
前者はPythonでのプログラミング初学者でも、forループを覚える前に教えても良いくらいの機能だ。いや、教えるべきだ。
そして、Pythonには全部を把握するのが困難なくらいのライブラリ関数があるが、何が何でもまずは使いこなさなければならないのがfunctools.reduceだ。
ハッキリ言おう。Python初心者を脱却出来るか否か、ってのはこのたった2つのポイントを押さえてるか否かで決まる。言い換えると、リスト内包表記やfunctools.reduceを使いこなせないヤツはPythonを「分かってない」ので人に教える以前の問題となる。
ここではまず、このfunctools.reduceを取り上げる。
例えば冒頭の差分方程式を見ると、n = 5の時、
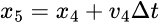
となる。そしてn = 4でのxを計算するには n = 3の時のxが必要となり、n = 3
でのxを計算するには・・・と初期位置まで計算する。
これをC言語やPascal、Java等ではforループを使って逐一代入計算で処理していくんだが、Pythonだとfunctools.reduceを使って次のように記述可能だ。
reduce(lambda x, y: x + v * dt, [1, 2, 3, 4, 5], x0)
ここでは、x0やv、dtの値は何か既に定義されてるものとし、Δtをdtとしている。
functools.reduceはギョッとするスタイルに見えるかもしんない。ラムダ式も入ってるし。
しかし良く見て欲しいのは、ラムダ式が指定している「計算」自体は全く差分方程式そのものだろう。
そう、functools.reduceの強み、ってのはわざわざ数式を分解してforループで回す、なんつーダサいことをせんで済むトコなんだ。ダサい計算法はC言語、PascalやJavaにさせとけばいい。一方、Pythonのfunctools.reduceを使えば計算式そのものを使って記述出来る。
ところで、[1, 2, 3, 4, 5]と言うリストは何なのか、っつーとコイツはカウンター代わりだ。そしてラムダ式は2引数関数になってるが、注意深い人はリストの中身が全く使われてない、と言う事に気づくだろう。
そう、nを表すカウンターは「計算式自体には何も影響を与えていない」。これは元々の差分方程式を見ても分かる筈だ。添字番号nは単に順序を示してるだけで計算の中身には介入していない。
なお、このケースでは、functools.reduceが返してるのは次の式だ。
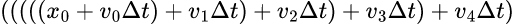
不安なら検算してみればいい。確かにn = 5のxの値(っつーか式)になってるだろう。
さて、functools.reduceの数値計算上の使い方は以上だが、ここで1つ問題がある。
上の議論から言うとn項目目までの計算はなるほど、functools.reduceを用いれば求まるだろう。
問題は、だ。そのnは一体何項目目まで、として計算すりゃあエエのか、って事だ。
最終的には斜方投射のアニメーションを作りたいんだが、初速幾らで角度幾らで投げて、一体何枚「原画」が必要なのか、と(笑)。
また、描画領域から出る、出ないの問題もある。これらも初速と角度から言うと変わるんで、結果到達距離とnとの関係が一般的には「全く分からない」わけだ。
さて、どうしたもんだろ、と。
結論から言うと「決めなくていい」。と言うか「決定を後回しにして」いいんだ。
僕らは既にその技術を知ってる。そう、遅延評価だ。
遅延評価だったらnは無限大でもいいわけだ。必要な部分だけ「あとで」切り取って持ってくればいい。
モダンな高級言語の一般的な旨味、っつーのは設計段階で「今は良く分からん事」を全て後回しに出来る事だ。言っちゃえば「最初に仕様を決めなくていい」。
取り敢えず計算だけはさせておいて、あとで、そこから必要な情報だけ抜いてくればいいわけだ。
ラクだろ(笑)?
ただし、そういう方針ならfunctools.reduceは使えない。代替手段としてfunctools.reduceの遅延評価版、itertools.accumulateを使う。
ここでもう一回、今回使う差分方程式を見てみよう。
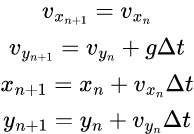
速度2つと二次元平面の位置情報2つがある。位置情報を計算するには速度の情報が必要だ。速度の情報を計算するには加速度情報が必要だが、今回は重力加速度gを使う。そして重力加速度は常に地球の中心に向かってるが、y軸は上向きを正にするんで、下向きにの重力加速度は負の数となる。その値は-9.8だ。
いずれにせよ、位置情報を計算するには速度の情報が必要になる。
よって最初に速度をitertools.accumulateを使って定義してしまおう。
vx = repeat(v0 * cos(degree))vy = accumulate(
count(),
func = lambda v, n: v + g * dt,
initial = v0 * sin(degree) + 0.5 * g * dt
)
degreeは角度を弧度法に直したものだ。具体的にはdegree = theta * pi /180 とする。また、piやcosやsinはimport mathすれば使える。
itertools.repeatは定数の無限長シーケンスを作る。水平方向には加速度がない。従ってx方向の速度は初速度の値を保ったまま、だ。要は、初速度の無限長シーケンスを作れば事足りるわけだ。
itertools.countは無限長シーケンスを生成する言い訳の為だけに入ってる。実際は数列の添字nを生成するが、かと言って速度算出の計算で使われてるわけでもない。ホント単なる「言い訳」だ。
もうひと工夫ふた工夫加えよう。速度はベクトルだった。ベクトルはPythonではリストないしはタプルで表現される。vxもvyも「速度ベクトルの成分」なんでタプルで纏めても構わない。これを実行するのがzipだ。
v = zip(
repeat(v0 * cos(degree)),
accumulate(
count(),
func = lambda v, n: v + g * dt,
initial = v0 * sin(degree) + 0.5 * g * dt
)
),
zipはイテラブルを受け取りイテラブルを返す。従って、無限長シーケンスを受け取り無限長シーケンスを返す。
もうひと工夫の方はy方向の速度の初期値の計算に於いてdtの値をその半分だけズラシている事だ。真っ向勝負だとここは v0 * sin(degree) だけでイイが、1/2 * dt分だけ先の計算結果にしておき、そうする事で全部の計算を1/2 * dt分だけズラす事が出来る。位置情報の計算でそれを使えば描画が格段に良くなるそうだ。 => 参考 : 計算機シミュレーション - sec10
無限長シーケンスvから値を取り出して検算するのならnextを使えばいい。
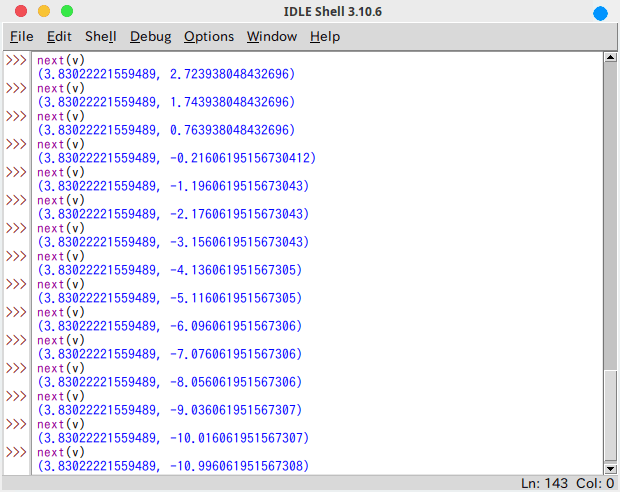
初速5、投射角40度、Δt = 0.1 での速度ベクトルの変化の例
キチンと速度ベクトルになってるだろう。
同様の方法で、位置情報は次のように算出出来る。
r = accumulate(v,
func = lambda r, v: (r[0] + v[0] * dt, r[1] + v[1] * dt),
initial = (0, 0)
)
ラムダ式内が一見ややこしいが、惑わされないように。位置ベクトルとしてタプルを返すようにしているが、各成分の計算式は上に挙げた差分方程式そのまま、だ。また位置情報の初期値(inital)はタプルで(x0, y0) = (0, 0)を意味してる。
vに直接速度の計算をぶっこみたかったらこうなる。
r = accumulate(
zip(
repeat(v0 * cos(degree)),accumulate(count(),
func = lambda v, n: v + g * dt,
initial = v0 * sin(degree) + 0.5 * g * dt
)
),
func = lambda r, v: (r[0] + v[0] * dt, r[1] + v[1] * dt),
initial = (0, 0)
)
まぁこの辺は好みだが(Lisp使いは不要な代入をしないので)、いずれにせよPythonでの数値計算自体はこれで終了、だ。
慣れない人は面食らうだろうが、遅延評価とreduceと言う考え方に従えば、何らかの物理量を分解して加算するのをforで回す、と言うようなかったるい事をせんでいい。数式のまま入力していけば自然と結果が得られる、と。
ダサいプログラミングはC言語(かFortran)に任せよう。Pythonなら、例えば数学的に差分方程式を得ればそれをそのままプログラミング出来て結果を見る事が出来るんだ。
ダッセぇ事やって回り道する必要もないわけだ。
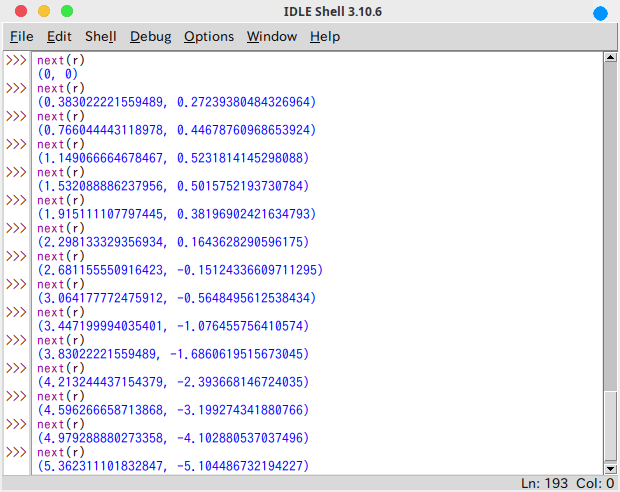
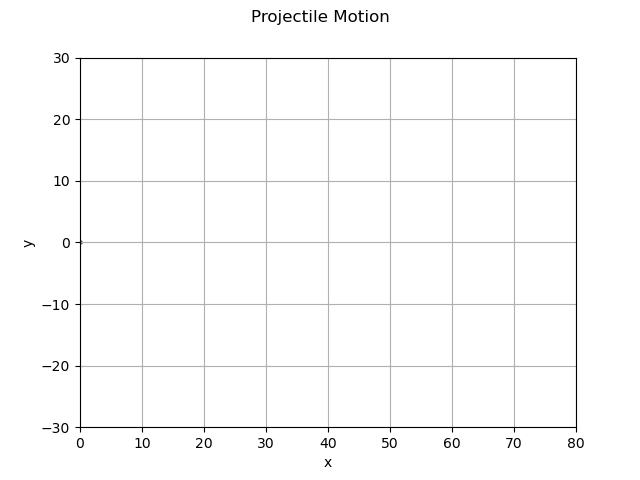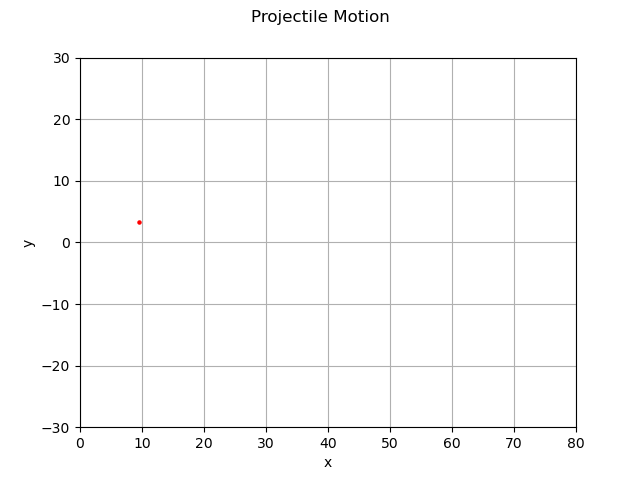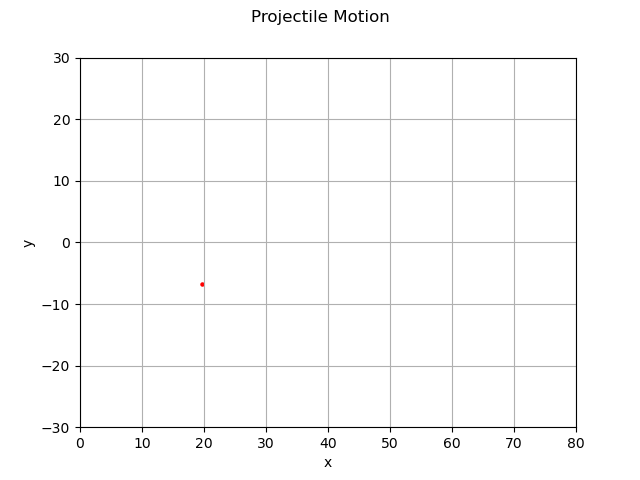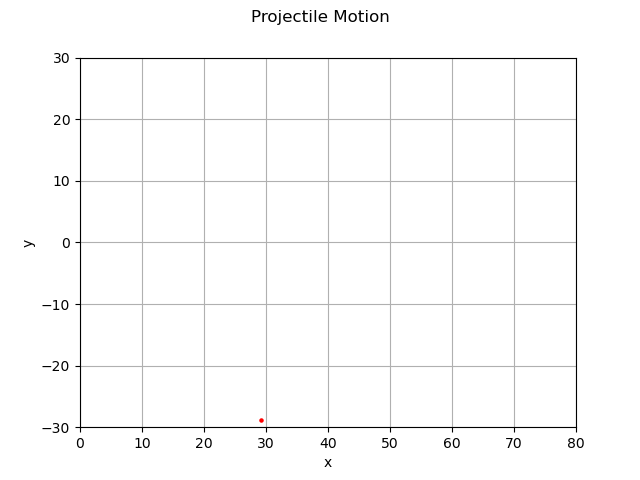
初速5、投射角40度、Δt = 0.1 での位置ベクトルの変化の例
さて、あとは基本的にはグラフ描画/アニメーション作成だけ、だ。
それはマニュアルの通りにやれば出来る。
が、ここでは英語が出来ない人の為に概要だけ書いておく。細かいとこは、日本語資料としてQiita辺りを見れば(役立つか立たないかはさておき)簡単に見つかるだろう。
今回使うのはmatplotlibと言う外部ライブラリのFuncAnimationと言う機能だ。
正直言うと、matplotlibはかなりクセのあるライブラリで、ハッキリ言って「使いやすさ」を主眼に置いては開発されていない。
「使いやすさを主眼に置いてない」と言うのは随分ヘンな開発方針に思えるだろう。実際問題、matplotlibは、科学技術計算用の商用製品、MATLABの描画機能の移植が目的のライブラリだ(※6)。
つまり、言っちゃえば「使いやすくする/しない」はMATLABの開発会社の責任であって、matplotlibは単純にその機能をせっせとコピーしてるだけ、だ(※7)。
FuncAnimationで描くアニメーションは大まかには次の4つで構成される。
- 静止画部分。x軸、y軸や格子等の描画部分作成。
- 動画用オブジェクト部分。動かしたいモノの定義。今回の例では「ボール」がそれに当たる。
- update関数。動画部分。この例だと「ボールの動き」を1フレーム1フレーム作成する。
- FuncAnimationで動画オブジェクトを作る。
1番は、このケースだと例えば、width、 heightの値を適当に定義して、次のように書く。
# Figure と Axes
fig, ax = plt.subplots() # 静止画部分生成
ax.grid() # 格子描画
ax.set(xlim = [0, width], ylim = [-height//2, height//2], xlabel = 'x', ylabel = 'y')
3行目でグラフの大きさやラベルを設定している。

1番だけでこういう「背景」をまずは得る。
2番は、このケースだと、「動く物体」ボールを作る。
# ボールの作成
ball = ax.scatter(*next(positions), 5, color = "r", label = f'v0 = {v0} m/s')
matplotlibで丸を描画する時にはscatterメソッドを用いる。初期位置x、 y、大きさ、そして色をここで指定する。
3番は2番で作成した「オブジェクト」を動画として処理するupdate関数を作る。具体的には2番で作ったオブジェクトの「位置情報」を破壊的変更で更新した後、そのオブジェクトを返すように書けばいい。
# ボールの更新関数
def update(frame):
ball.set_offsets(frame)
return (ball,)
実はマニュアルがかなり書き方としてマズい例になっている。
この更新関数の引数、frameと言うのは実は「描画したいデータ」、要は今回の場合「ボールの位置情報」のデータでいい。
しかし、マニュアルではそれを大域変数にしてて、それを利用する、と言う悪例になってるんだ。
4番目でこの辺、ちょっと説明しよう。いずれにせよ、元ネタになったMATLABは言っちゃえば「マトモなプログラミング言語実装」を目指して作られたモノじゃない。「数値計算スクリプト」を意図してるだけ、なんで、「計算さえできれば良い」と言う割り切った設計になっていて、Pythonのように「オブジェクト指向プログラミングをサポートする」とか「関数型プログラミングをサポートする」と言うような意図はない。
だから唐突に「大域変数を利用する」と言ったような手段を取り、このマニュアルもそういう「MATLAB流儀」から来てるんだろう。
ちなみに、update関数は「必ず」タプルで値を返す。
と言うのも、今回は違うが、複数の物体を同時に動かすのもこのupdate関数1つで行う為、更新した複数の物体を同時にタプルで返す必要があるから、だ。
4番目がアニメーションオブジェクト生成だ。具体的にはFuncAnimation関数を引数付きで呼び出す。この例だと例えばこんなカンジになる。
# アニメーション作成
anim = FuncAnimation(
fig,
update,
frames = positions,
interval = 1000 * dt,
blit = True
)
第一引数はバックグラウンドを含めた静止画指定で、1番で作ったfigを入れる。
第二引数は3番で作ったupdate関数をクロージャとして指定する。
キーワード引数「frames」ってのがまた紛らわしい名前なんだけど、事実上、これはupdate関数に与える引数だ。引数のスタイルとしてはコンテナ(つまり、リスト、タプル、遅延シーケンス、NumpyのArray)なら何でもいい。
重要なのは、FuncAnimationはそれらコンテナの先頭から1つ1つ要素を取り出してはupdate関数に手渡していく事、だ。従って、ここに「数値計算」で作成した遅延シーケンスを渡せばいい。
intervalはややこしいが、いわゆる「動画」に於ける、こっちの方が「フレーム」だ。1枚目の「フレーム」から2枚めの「フレーム」までの待機時間を指定する。
matplotlibもそんなに速くないので、上限は1秒で25フレームから30フレーム辺りなんだけど、それを結果ミリセカンド単位で指定する。大体、25フレームで40msってトコなんで、それ以下にしたトコでmatplotlibの「性能上限値」を超えてしまって無駄となる。
blitは高速描画のオマジナイで、Trueを与えておこう。
さて、最後に、これは「数学的スクリプト」なんだけど、初速度や投射角度をどうやって与えるか考えてみよう。
良くあるテとしてはinput関数で初速度や投射角度を入力させる、って方法がある。
が、ここでは「スクリプト」なんで、端末からこのスクリプトを引数付きで呼び出し、そしてその「スクリプト」のコマンドライン引数として初速度と投射角の2つを与える、って事にしよう。
また、グラフの横軸と縦軸にどれだけ目盛を出すか、とか高さの初期値をどうするか、なんつーのも、Pythonの関数での「キーワード引数」みたいに、デフォルト値はこれこれ、なんだけど、キーワード引数を与えたら「変更可能」みたいにしてみよう。
そういう「コマンドライン引数の一種キーワード引数化」に役立つライブラリがargparseだ。
argparseの使い方はチュートリアルに書いてるんでさほど難しくはないだろう。
ここでは次のように書いてみる。
parser = argparse.ArgumentParser()
parser.add_argument('v0', help = '初速度', type = float)
parser.add_argument('theta', help = '入射角', type = float)
parser.add_argument('-w', '--width', help = '横軸', type = int, default = 8)
parser.add_argument('--height', help = '縦軸', type = int, default = 6)
parser.add_argument('-dt', help = '微小時間', type = float, default = 0.04)
parser.add_argument('-y0', help = '初期位置(高さ)', type = float, default = 0)
parser.add_argument('-s', '--scale', help = '倍率', type = int, default = 10)
if __name__ == '__main__':
args = parser.parse_args()
width, height = args.width * args.scale, args.height * args.scale
ここでは初速度と入射角の2つだけ、が必須の引数で、他はいわゆるデフォルト引数として設定されてる。そして、widthとheightの2つが目盛の下限と上限を決めるが、同時にここでの決定が、無限長シーケンスから「どの範囲」を切り取ってくるのか、のヒントとなる。具体的には0 ≦ x ≦ width、-height/2 ≦ y ≦ height/2が切り取ってくる範囲だ。
# x, y 座標計算
positions = takewhile(
lambda r: r[0] >= 0 and r[0] <= width and
r[1] >= - height/2 and r[1] <= height / 2,
accumulate(
zip(
repeat(v0 * cos(degree)),
accumulate(
count(),
func = lambda v, n: v + g * dt,
initial = v0 * sin(degree) + 0.5 * g * dt
)
),
func = lambda r, v: (r[0] + v[0] * dt, r[1] + v[1] * dt),
initial = (0, y0)
)
)
数値計算の結果である無限長シーケンスからitertools.takewhileで必要範囲を切り取ってくる。これが「後回し」の部分だ。
微小時間Δtによって必要なシーケンスの「長さ」も違うし、「描画範囲」も変わってくる。そして「描画範囲」さえもユーザーの都合で変更になる。
結果、「どういった長さのシーケンスを」FuncAnimationに手渡さなければならないのか、ハッキリ言っちゃえば「プログラム実行時」まで分かんない。
一方、遅延評価なら「決定は全て後回し」なんで、長さを最初に決めなくても「何とかなる」わけだ。
これがいわゆる「グラフ描画込みの数値計算」に於ける遅延評価使用の強み、だ。決定したくない部分は全て後回しで構わんわけだ。
あとは、同じくargparseで定義したデフォルト値で必要となる変数を設定しておけばいい。
# 初期条件設定
dt = args.dt # 微小時間
y0 = args.y0 # 初期 y 座標
v0 = args.v0 # 初速度
degree = args.theta * pi / 180 # 入射角
g = -9.8 # 重力加速度
これで完成、だ。ソースコード全体はここに置いておこう。
繰り返すが、「C言語のように書く」ならPythonは必要ない。「C言語のように書く」なら当然C言語を使うべきだろう。
言い換えると「Pythonと言う武器を使う」と言う事は、必然的に「数値計算」のスタイルも変わる、って事だ。
また、「遅延評価」と言う武器も一般的なプログラミングでは使いどころが分かりづらい。慣れる慣れない以前に「使えない」んだ。
一方、数値計算は、実はやってる事自体はさほど高級でもなく、プログラミングとしては目的もハッキリしてるし「機能」の実験がしやすい。
そしてC言語脳は全く把握してないけど、「数値計算」と「遅延評価」は実はかなり相性がいいんだ。遅延評価を実験するなら数値計算でテストすべきだ、ってのは以前にも指摘した。
今回もその単純な一例だ。
数値計算を通じて遅延評価に慣れる人が増える事を望む。
※1: ここでもこのテの問題に対して論じてる。
※2: 当然予想通り、加速度が時間の関数の場合もある。
※3: 自然科学と違い、数学、と言うジャンルでは実は「発見」は極めて少ない。
と言うのも、数学は自分で何かを定義して、自分でそれを使った定理を見出し、無矛盾な体系を作り上げれたら良し、と言う学問で、極論全ては人の手のひらの上にある。
言い換えると偉大なるマッチポンプと言うのが数学の本質的なトコで、結果「人間が知らない何かを発見した」と言う例は極めて少ない。
そんな中で珍しい「数学上での発見」が微分だったわけだ。
アイザック・ニュートン(1643〜1727)は17世紀に微分法を発見したが、数学的に見ると「0で割る」微分法は極めて怪しい手法で、19世紀に決着が付くまで、「数学的に見て怪しいのは分かっちゃいるけど」状態で発展してきた。言い換えると、100年以上「怪しいままで」使われてきたわけだ。
これは数学史上、かなり珍しい発展方法だ。
有名な俺らのオイラーさんも18世紀の人で、この人も微分法に多大な貢献をした人なんだけれども、「微分法の根本は怪しいけど」状態で色々と研究してくれたわけだ。
18世紀だと微分法は「根本が怪しいけど、どうやら多分正しそう」状態なわけで、そんな中で微分法に「賭けた」オイラー氏はとんだ博打打ちだ(笑)。だって、根本が間違ってたら業績がパーになる可能性が常にあったわけだからな。賭けに勝ったから良かったんだけれども。
なお、ニュートンが微分法を世に問うたのは書籍「プリンキピア」だが、採用したのは幾何学的な手法で、根本的には件のgifアニメと丸っきり同じだ。
「作図で描ける以上そうならざるを得ないでしょ?」
と言って逃げている(笑)。
※4: 単に速さ、と言った場合はそれは理論上の値、と言う事で実測上の値じゃない。理論上の話、と言うのは要は数学上の話であり、速さ自体は基本的には現実的には直接得られるナニカじゃないんだ。
「あれ、でも車とかにスピードメーターとか付いてるじゃない?」
と思うかもしれないが、実はあれで得られるのも「平均の速さ」だ。
Δtを人間が感知出来る1秒以下の短い秒数にしておき、車輪が「どのくらい回転したか」、つまりやはり二点間の移動とΔtを使って「はじきの法則」で割り算して求める、と言うのが原理だ。
要はこの記事で扱ってるような方策と原理的には同じだ。
なお、野球で使うスピードガンなんかは別の方法を使って「間接的に」大谷が投げたボールのスピードを得ている。
※5: 実は数理的には議論が逆で、ベクトルである速度が基準で、速度の「大きさ」を速さと呼ぶ。
ただ、「はじきの法則」は小学生向けのアンチョコであり、小学生はベクトルの概念を知らない。
※6: 科学技術計算ではFortranとMATLABが二大デファクトスタンダード言語だと考えていい。ただし、Fortranは基本的にプリミティヴな計算用で、一方、MATLABは行列演算をベースにしている辺りが設計思想として違う。
MATLABのフリーソフトとしてのクローンは、GNU OctaveとScilabが有名だったが、ここに来て、Pythonが(外部ライブラリの力を借りて)台頭してきてる。
※7: 平たく言うと、Pythonの数値計算用ライブラリ、NumpyもMATLABクローンとして作られている。














