パスカルの三角形とは次のような図で表される数の列・・・って言えばいいのか、とにかく三角形型のダイアグラムだ。

実は何てことはない。頂点と辺を形成してる1はともかくとして他の数は丁度上にある2つの数を足したものとなっている。
たとえば、3は上にある1と2、あるいは2と1を足した数になっていて、10は4と6、あるいは6と4を足したモノとなっている。
これが有用なのかどうか、ってのは一考の余地がある、っつーか、簡単なルールで形成されてる三角形、と言うのは単純におもちゃとして面白い。
もう1つの特徴は、2つの数の和、及び差、のn乗を展開して出てくる式の項それぞれの係数になってる、と言う辺りだ。
例えば、中学校数学でお馴染みの
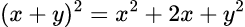
と言う展開に於いて、右辺の各項の係数はパスカルの三角形の(頂点を0段として)2段目の数値の組、(1, 2, 1)と一致してる。
高校数学で習う
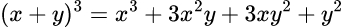
もそうだ。展開形の各項の係数はパスカルの三角形の3段目の数値の組、(1, 3, 3, 1)と一致してる。
つまり、(x + y)のn乗を計算しろ、って言われた時、アンチョコとして効力を発揮するんだな(笑)。必要な段を探してそれらを適用すると、人力でうんうん唸って計算せんでも、答えが一瞬にして分かる。これは便利だ。
また、数学上の要請により
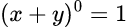
だし、当然
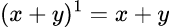
なので矛盾も破綻もしてない。万々歳だ。
さて、このパスカルの三角形を計算するコードを書くとする。
色んな方法があるとは思うが、取り敢えずここでは次のようなコードをまずは書いてみよう。
(define (f lst)
(let loop ((a (car lst)) (b (cadr lst)) (lst (cddr lst)) (acc '()))
(if (null? lst)
(cons (+ a b) acc)
(loop b (car lst) (cdr lst) (cons (+ a b) acc)))))
パスカルの三角形の「段」をリストとして見做した場合、取り敢えず端っこはどう逆立ちしようと1になるんで、その辺は後回しにする。問題は1と1に挟まれた部分だが、これを計算する「エンジン」が上の再帰関数fだ。
しかし内情は難しくない。あるリストを与えられた時、その先頭とその次の要素を足してそれをアキュムレータにconsしていく。あとは2番目の要素を先頭にズラし、残りのリストから2番目の要素として先頭を取り出してくる。その繰り返しだ。
実行結果を見てみよう。
> (f '(1 2 1))
'(3 3)
> (f '(1 3 3 1))
'(4 6 4)
> (f '(1 4 6 4 1))
'(5 10 10 5)
>
計算結果は別にパスカルの三角形そのものじゃあない。ただし、重要部分のリストを作り出してるのは分かるだろう。言い換えると先頭とケツに1を付け加えればそのままパスカルの三角形の「段」となる。
これさえ書いちまえばパスカルの三角形を丁稚上げるのは簡単だ。
次のように書く。
(define (pascal n)
(let loop ((n n) (acc '((1) (1 1))))
(cond ((zero? n) `(,(car acc)))
((= n 1) acc)
(else (loop (- n 1) `(,@acc (1 ,@(f (last acc)) 1)))))))
名前付きletで再帰するが、アキュムレータの初期値でインチキをする。ここに最初の二段を仕込んでおく。言わば、計算上、こいつらはちと例外っぽいんで、最初っから定数っぽい扱いにしてた方がいい。
実際の停止条件、ベースケースは1段目、って事になる。nが0のケースは単に、外部から引数に0が与えられた場合、帳尻を合わす為に置いてるに過ぎない。
実際の再帰は言わばお馴染みなんだけど、これで準クオート及びコンマ@の威力が分かるだろう。先程書いた関数fは除くにせよ、パスカルの三角形の「段」を構成する為に地味ながら威力を発揮してる。ここだよな。
(1 ,@(f (last acc)) 1)
これにより、fで計算した結果のリストの「カッコを外し」、そして先頭と末尾に同時に1を付け加え、パスカルの三角形の「段」を製造してるんだ。
ここを準クオートとコンマ@ナシで書こうとすると、物凄く煩わしくなるのは想像に難くないだろう。
これで、10段目までのパスカルの三角形を計算すると次のようになる。
> (pascal 10)
'((1)
(1 1)
(1 2 1)
(1 3 3 1)
(1 4 6 4 1)
(1 5 10 10 5 1)
(1 6 15 20 15 6 1)
(1 7 21 35 35 21 7 1)
(1 8 28 56 70 56 28 8 1)
(1 9 36 84 126 126 84 36 9 1)
(1 10 45 120 210 252 210 120 45 10 1))
>
繰り返し自体が両者ともに「末尾再帰」で書かれてる為、大して計算負荷はかからず、一瞬で計算が終わるだろう。
また、僕流に言わせてもらうと、このテの計算に「出力」がどーの、なんつーのは考えなくても良い。仮に整形出力が必要だとしたら、そういうのは「全て後回しで構わない」んだ。
必要なのは作成した「データ」だ。データさえあればどう出力しようが、後回しでも思いのまま、なんだ。
参考: ソースコード例














