星田さんの記事に対するコメント。
ラジアン。大昔にBasicの本で見た記憶があるなぁ・・ふうむ・・計算の都合上便利な(事がある?)ので使う進法の違いみたいなものか?

それはドリアンだ(謎
ラジアンは単純に角度の事。
小中学校だと180度、とか言ってたけど、180度をπと言う数値に対応させようぜ、ってそれだけの話。つまり、360度は2πになる。それだけ。
ちなみに、最近の高校生だとラジアンやってないかもね。今は大学入ってから学ぶのかもしれない。
ところで、こういう風に簡単に単位を「変えちゃって」いいのか、って話があるんだけど、実はやって良い。っつーか本当の話をすると、角度はどんな数値を当てはめても実はいいんだ。大きさは勝手に自分が定義しても構わない。
ただし、「共通言語」で話したい場合、自分が考えてる「オレサマ単位」と他人が考えてる「オレサマ単位」が違ったら困るでしょ、ってだけの話って言えば話(※1)。
そして実のこと言うと「角度」ってのは突き詰めると「比」なのね。比率の「比」だ。それで言っちゃえば「比」ってのは単位を持たないんだよ(笑)。単位のフリしてる単位なんだ(笑)。こういうのを無次元数と呼ぶ。
例えば速度の場合、定義は「距離/時間」だ。「距離」も「時間」も別々のもの(量)なんで、割ってもキャンセルされない。同様に、面積は「距離×距離」なんでこれも単位としては「そこにある」わけだな。
ところが、角度ってのは比率、つまり「距離/距離」なんだ。距離を距離で割ると「距離」ってものは消えてしまう。つまり何らかの物理的な「量」ってのはキャンセルされちゃうわけ。こういうのを「無次元数」って呼ぶんだな。
一般に、例えば百分率で、食塩水の問題、とかあるでしょ?水xグラムに塩yグラム混ぜてzグラムの食塩水を作れ、と。で、計算問題としてはそれでいいんだけど、ここで言うトコの「%」が何なのか、と言うとこれも無次元数なわけ。重さを重さで割る以上、単位としては実は「何も無くなっちゃう」んだな。
こういう無次元数の場合、「オレサマ単位」を作ろう、って思ったら、根底的には「別になんでも良い」ので自分で好きに単位を定義する事が出来る。まあそうしたら他人と意思疎通するのが難しくなるんで、まぁ、オフィシャルに従う事にしましょうよ、ってだけの話なわけだ。
繰り返すけど、角度は無次元数だ。それで歴史的には一周回って360度、とかやってきたけど、数学的にちと使いづらいトコがチラホラあるんで、360度を2πとしようぜ、と言う約束を決めた、って言うそれだけの話なんだ。
あ、sinってそういう事か!なるほど・・パッと思いつくのはゲームの当たり判定とかに必要なのかな?
っつーかまずは座標計算かしらん。
慣例的にはx, y座標に於いて
- x = rcosθ
- y = rsinθ
の関係がある(rは原点から座標への距離、θはx軸とrが成す角度)。
お互い変換しながら計算、ってのが良くあるかな。まぁ、ゲームに拠るけどね。
あと、是非とも覚えておいて欲しい式はあまりに有名なこれだ。

「数学史上最も美しい式」と言われてる、通称「オイラーの公式」。ネピア数の虚数乗はcosと虚数×sinの和になる、と。


x = πの時、この漫画で語られてるような式になる。
まぁ、直接プログラミングに出てこないかもしれないけど、教養としては押さえておいた方がいいし、微分方程式なんかのプログラミングをする際にひょっとしたらお世話になるかもしんない。
でtanってのは傾きか・・うーん・・実際に必要になりそうなシチュエーションは・・?うーん・・坂道の移動で加速が必要かどうかの判定とか?応用先を考えたりすると身に付きやすいかもなぁ・・他人事じゃなくなるんで。
うん、まぁ・・・そうね、cosやsinに比べるとイマイチtanは出番はないかもしんない。
tan自体よりもarctan(tanの逆数)の方がプログラミングだとお世話になるかな。例えば、x, y 座標があったとして、この点と原点、そしてx軸で成す角θを求めよ、とか言われた場合、通常プログラミングでは
- θ = arctan(y/x)
で計算する。
他にも、arctanのグラフはもっとも簡単なシグモイド曲線、ってぇんで色々と使える。

こういうS字を横に引き伸ばしたような曲線をシグモイド曲線、っつーんだけど、ちょっと弄って最大値を1、最小値を0にするようにしたら、昔の家電で良く聞いた「ファジー理論」とかで使った「ファジー」を表せる(笑)。
あと、人工知能で有名な「ニューラルネット」もこのテのシグモイド曲線を組み合わせて作ったりする(脳のシナプスが送る「電気信号」をこのシグモイド曲線で表現する、ってのが古く基本的なアイディアだ)。
この一番簡単な例がarctanが形作る曲線で、結果、tanよりも逆数のarctanの方がプログラミングではお世話になるかもしんねぇな、と言うお話(※2)。

ふーむ・・公式3がややこしいかな。log x log x log であって3 x logじゃないんすね。で?
いや、公式③は公式①と実質同じだ。

とMをk回掛けたものなんで、①の公式を適用すると
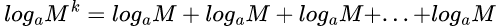
となる。結果logの部分がk個ある、って事なんで③が証明される。
なお、log×log×logだとlogの3乗になるんで、この公式群には含まれません。
でw?

ほぉ〜・・・って、これコンピューターあったら別にいらなくない?計算をしやすくするだけ?しかも元になる表ありきの話だし
ごめん(笑)。Lispが便利過ぎてあまり対数の有り難みってのが分かんないでしょ(笑)。
そう、これはLispが便利過ぎる弊害なの。
まずよ。対数とは。
そもそもこれってルーツは数学じゃねぇんだわ(笑)。誰がこれを使ってたのか。それは商人が使ってたツールなの。
貿易をガンガンやってると信じられない額の金が移動するわな。整数でこれら「大金」を計算するのが厄介になってきた。桁数がとにかくデカい。なんとかこの「桁数」そしてその変動を押さえ込めねぇか、と。
そこで整数を「対数変換」すると小数点数が出てくるんだけど、桁数の変動がガクッと押さえ込める事を商人の連中が発見したんだな。そして対数計算表を使えばアンチョコで計算出来る、と(※3)。

対数を計算する「計算尺」と言われる計算機。17世紀に発明され広く使われた。17世紀はイギリスがインドに東インド会社を設立、またアメリカ大陸に入植が始まり、貿易圏の拡大が行われた時期である。

そう、この「桁数の増加を防ぐ」ってのが対数の大きな効果なんだ。
でだな。
Lispは非常に高性能のプログラミング言語なんで、理論的な話をすれば、「どんなデカい大きさの整数でも」メモリさえ許せば扱えるように設計されている。
ところが世の中には「桁数の上限」とか決められてるプログラミング言語もあるわけよ。C言語とかな(※4)。
再帰の基礎的な練習問題に階乗計算がある。
問題: 整数nの階乗を計算する関数factorialを書け。
まぁ、こんな問題はハナクソだ。
Lispで書けば次のようになる基礎的問題だ。
(define (factorial n)
(let loop ((n n) (acc 1))
(if (zero? n)
acc
(loop (- n 1) (* n acc)))))
これで終わり、だ。
ここで例えばnに10を与えてみよう。
> (factorial 10)
3628800
>
うん、簡単に計算出来るよね。
・・・・・・でもちと待って欲しい。
Lispは高機能だからこれでいいけど、たった10項目目で階乗の計算結果は三百六十二万八千八百だぜ?繰り返そう。三百六十二万八千八百だ。桁数は7桁だ。
「Lispだから」こういうデカい数値を簡単に出してくれる。
でも?仮に整数の上限が決まったプログラミング言語なら?あっという間に「計算不可能」って結果になるだろう。
まぁ、整数に「変換する」ってのはまた別にメンド臭いテクニックが必要にはなるんだけど、それ以前に「階乗」を計算出来ないと画餅になっちまう。整数に厳しい上限があるけど、計算「自体を」なんとかしなきゃなんない場合どうすんだ?
誤差が出るにせよ、ここでやるのが「対数変換」だ。そうすれば、桁数が膨れ上がって計算が不可能になる事はない。
(define (factorial n)
(let loop ((n n) (acc 0)) ;;; log1 = 0 の為
(if (zero? n)
acc
(loop (- n 1) (+ (log n 10) acc))))) ;;; 乗算が対数により加算になる
> (factorial 10)
6.559763032876794
> (factorial 1000)
2567.6046442221323
> (factorial 10000)
35659.45427452077
>
n に 10を与えた時、元のコードだと三百万を突破した数値を返していたが、対数変換されれば1桁+小数点以下で納まる。当然、1000や10000を与えるともっと爆発的に巨大な整数が返ってくる辺りも、対数変換すれば比較的「緩やかな」桁数の範疇に納まるのが分かるだろう。
もちろん、本当の階乗計算の結果は10の6.559763032876794乗とか、10の2567.6046442221323乗とか、10の35659.45427452077乗なんだけど、「底が10」と言う事さえ分かっていれば、この情報だけで充分、って言えば充分なんだ(※5)。
とにかく「巨大な数値を扱う」のがメンド臭い場合、対数に変換する、と言うのが威力を発揮して、それが故に商人が好んで使ってた、と言う背景があるんだ。

ふーむ・・データの中に実行させるコードをぶっ込んでるって事か・・(多分)。全然抵抗は無いな・・特定の機能も果たす関数っぽいのと一緒に統一した書式でデータにして整理して保存してるんで、呼び出し部分も見通しが良くなるってことかな?と、間違ってても一応推理をしてから読むと良いらしいので・・
その通り。
特に目新しくはないでしょ?今までチマチマやってた事に「名前を付けた」程度だし。
で、同時に、どうせラムダ式を扱うならこういうトコに到達せんと意味がないよね、とそういう辺りでもある。
Lispはそういうテクニックにユーザーを簡単に誘うんだ。
> 2022/07/27
例のLambdaを使ったクラスっぽいアレ、Shemeだとどうなるのかな?とやってみたけど、引数の初期値を与えておくってのが出来なかったっぽい?それやめたら動いたかな、と。
あー、ごめんごめん。
そうね、オプショナル引数ってのはSchemeの仕様範囲外だったわ。すっかり忘れてた(笑)。

Gaucheでオプショナル引数を使う場合には、:optionalと言うキーワードを与える。そのキーワード以降は全部オプショナル引数だと解釈される。
Racketの拡張とは方針が違うんだけど、割にGaucheの場合、独自拡張やる際にはこう、ANSI Common Lispっぽい拡張を試みるカンジかな。
なんつったって、川合史朗さん、Scheme実装作ってるけどCLerでもあるからね。CLっぽい便利な機能はガンガン輸入してきます、ってカンジですしおすし。
※1: これで国際単位系、と言う単位を決める必要が出てきたわけだ。無次元数だろうとそうじゃなかろうと、共通規格を決めておかないと何の話をしてるかサッパリ分からなくなるからだ。白人が1ガロン、つってんのに日本人が一升で話するとお互い何の話してるんだかサッパリ分からなくなるから、だ。
なお、長い間イギリスは国際単位系に従わなかったが(決めたのが仲が悪かったフランスだからだ、って話がある・笑)、最近では国際単位系に従うようになってて、今現在、ヤードだマイルだフィートだガロンだポンドだ、とか使ってるのはアメリカだけなんじゃないか。
※2: 他にも整数乱数で出た値をyとして、対応するxを「乱数の結果として返す」と言う使い方も考えられる。正規分布に従う乱数にはならないが、かなり近い結果になるのではなかろうか。
※3: 底が10の対数を常用対数と呼んだりする。一体誰が常用するのか。元々は言外に「商人が常用する」と言う意が含まれている。商人が扱う「お金」は10進法で数えられるからだ。
現代では、数理科学者は底にネピア数eを用いる事が多い。これは微積分がやりやすいから、である。
※4: 最近のPythonもやっと上限値が無くなったが、以前のPythonだと上限値が決められていて、そこを超えると数値の末尾にLが付加されていた。
なお、C言語だと昔懐かしい16ビットPCだと上限値は32,768になる。
「あれ?桁数上限じゃないの?」
と思うかもしれないが、桁数上限だ。と言うのも16ビットPCだと2進数で15桁が上限になるから、だ(残り1ビットは負の符号を表す・・・「符号付き整数」だと、だ)。同様の理由で32ビットPCだと桁数の上限は二進数で31桁、と言う事になり、このようにC言語はハードウェアの能力に整数上限値が左右される。
※5: と言うのも乗数では例えば

となり、右辺の第一項はそのまま1,000,000となり、10の0.559763032876794乗に百万を掛けたもの、と言う事になる。
そうすると、有効数字の問題はあるが、いずれにせよ「どんな数が含まれるのか」は10の「小数点以下の数」乗が握ってる事になる、ってのは明らかだろう。













