【初音ミク】 日立の樹 / この木なんの木 (Quel Type D'arbre Est Cet Arbre?)
この木なんの木、って問われれば、答えは平衡二分探索木、がGLibのGTreeだ。
結果、これをデフォルトで搭載してるプログラミング言語自体が「新しい」プログラミング言語じゃないとなく、僕自身もHaskellくらいしか知らない。しかも、本質的には破壊的操作に頼る事になり、非破壊的なHaskellに於いて、どういう実装になってるのか興味が尽きなかった。
そんなんで僕個人では平衡二分探索木に興味があったわけだが。
GLibを導入すると、この「新しい方のプログラミング言語じゃないと搭載されていない」平衡二分探索木を使いまくれるようになる、ってのはメリット以上のメリットだろう。
また、プログラミング言語に於いての「連想配列」の実装法として見ても、ハッシュテーブルに対抗できる平衡二分探索木は明らかに良い候補だ。
GLibでは平衡二分探索木以外にもフツーの木を扱えるが、平衡二分探索木を中心に取り扱っていこう。

まずGTreeのコンストラクタはg_tree_newだ。こいつで平衡二分探索木を生成する。
以前見たが、原則的に、二分探索木の場合、キーの大小によって値の配置を決めていくんで、二分探索木を生成する時点で、「比較関数」を指定しないとならない。g_tree_newも当然その流儀に従っている。ここでは、ascii文字列(char*)の比較関数g_ascii_strcasecmpをGString用に拡張したg_str_ascii_strcasecmpを作成して、それを比較関数としてGTreeをコンストラクトしてる。
GTreeにデータを挿入する際にはg_tree_insertを使う。
g_tree_insertは木を破壊的変更するプロシージャだ。要は返り値はない(void)。第一引数は挿入対象の木、あとはキーと値を指定する。
木の高さを調べるにはg_tree_heightを使う。
返り値は当然生成してる木の高さ(整数: gint)になる。
木に含まれる節(ノード)の数を数えるにはg_tree_nnodesを使う。
ノード数を数えるのは結構メンド臭い(笑)。以前やった探索技法を使って含まれるノードを数え上げないとならないから、だ。よってビルトインで用意されてると結構嬉しい(笑)。
返り値は当然gint型(整数)となる。
GTreeから要素を削除するにはg_tree_removeを使う。
第一引数に対象となる木を指定、第二引数に削除したいキーを指定する(キーが指定されれば当然、関連付けられた値も削除される)。
返り値は真偽値(gboolean)だ。キーが見つかればTRUEが返されて「キーと値のペアが削除された」事が分かる。仮に「存在しないキーを指定してたら」FALSEが返る。
木に含まれる全てのノード(キーと値のペア)を削除するにはg_tree_destroyを使う。
以上が基本的なGTreeの使い方、だ。
実行結果

ここではもっと細かく設定出来るg_tree_new_fullと言うコンストラクタを用いている。
g_tree_new_fullは比較関数指定の他に、比較関数に渡すデータ(無い場合はNULLを渡す)、そしてキーや値を削除する際に使用するメモリ解放関数(free系)を指定する事が出来る。ここでは敢えて出力関数key_dとvalue_dを作ってそこに登録し、ノードにある操作をした場合、登録された関数が「呼び出されるかどうか」の様を見てもらっている。
g_tree_replaceはg_tree_insertの対になる関数で、ノードを丸ごとキーと値のペアと取り替える。
返り値はなく(void)、また、これが実行された際に、g_tree_new_fullで設定されたキーと値用のfree系関数が呼び出される。
一方、g_tree_stealはキーを指定しただけ、で関連付けられた値も含めて削除されるが、g_tree_new_fullで指定されたキーと値用のfree系関数は呼び出されない。
返り値は真偽値(gboolean)になっているが、指定されたキーが見つからなかった場合、実質的に、この関数は何もしない。
「スティール!!!」(違
次は検索関数だ。
検索関数は二種類ある。
1つ目の検索関数はg_tree_lookupだ。
第一引数は木、で第二引数がキーとなる。返り値はgpointerだが、キーが見つからな方場合、返り値はNULLになる。
もう一つの検索関数がg_tree_lookup_extendedだ。
これは、Lispのように多値を返す「つもりの」意図で設計されている。しかし、Lispのように多値が返せないので、外部的に変数を2つ用意して、それをダブルポインタで指定して結果を「代入」するようになっている。対象は検索対象になったキー、そしてそれと関連付けられた「値」だ。
なお、キーが見つからなかった場合、FALSEが返る辺りがg_tree_lookupと違う辺りだ(結果返り値自体は真偽値だ)。
次はg_tree_for_eachだ。こいつはスゴイ。
Lispなんかでもfor-eachはお馴染みの関数だけど、「木対象」なんつーのはない。
そもそも、Schemeなんかではリスト相手、となると豊富な操作関数が存在するが、一方、「木」と言うテーマだとSRFIをひっくり返して探してみても見つからなかった。
一応、このブログでも探索、と言うテーマは扱った事があるが、木関連でのmap、とかfor-each及びreduce/foldなんつーのは是非とも自作ライブラリを作る際には作っておきたいユーティリティだ(Racketの有志によるライブラリにはそれっぽいものもあるが)。
いずれにせよ、木用のfor_eachが存在する、ってのは痒いトコに手が届くライブラリ構成だ。
g_tree_for_eachは木から順繰りに取ってきたノードと、第三引数に与えられたuser_data対象(必要ない場合はNULL)に、第二引数で与えられたfuncを適用していく。なお、第一引数で指定された「木」を改変する能力はない。
なお、第二引数で与えられたfunc(コールバック関数)次の形式に従う必要がある。
返り値はgboolean、そしてキー、値、(何らかの)データ、の3つの引数を取る関数だ。
ここでは、iter_all、iter_someと言う単なる出力目的の関数を2つ定義している。
また、g_tree_for_eachは「途中で止める」事が可能で、それはコールバック関数が真を返した時、だ。逆に言うと、コールバック関数が偽を返し続ける以上、g_tree_for_eachは木の探索を止める事はない。
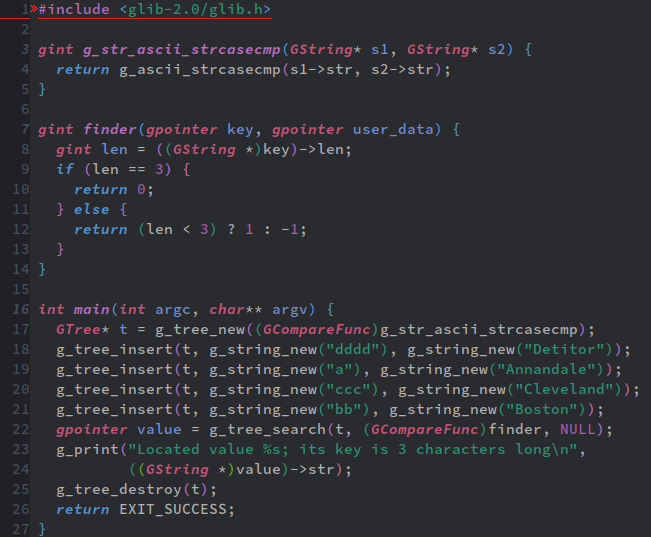
大方の「検索」ではg_tree_lookupで間に合うが、もうちょっと複雑な条件で検索したい、と言う際に使うのが、g_tree_searchだ。
ここではキーの文字列の長さが3である時の値を調べている。
g_tree_searchは三引数関数で、第一引数は検索対象の木、第三引数はオプショナルのデータで両者のデータが第二引数のコールバック関数へと渡される。返り値はgpointerだ。
第二引数のコールバック関数は比較関数で、次の要請に準じる。

返り値は整数(gint)で、引数は2つ。どちらともgconstpointerだ。第一引数が指し示すブツが第二引数が指し示すブツより小さかったら負の数、同じだったら0、大きかったら正の数を返す。それが要請となる(と言う事は、仕様的には正の数が1、負の数が-1である必要は必ずしもない)。
上の例だと、finderと言う関数を書いてるが、実は第二引数自体は無視してて、与えられたキーをGString型と確定させたあと、長さを取り、それが3と比較してどうか、と言うトリックになっている。
さて、ここまでは二分木だったが、最後にN分木を扱う。
厳密に言うと、GTreeは二分木で、N分木はGTreeではなくGNodeと言う別のデータ型を扱う事となる。
また、実装上、「木」と言いながら親子の関係は次のようになってるらしい。
つまり、「親子関係」は一つのエッジしかなく、「複数の子」がいた場合、親が直接認識しているのは「長男」のみで、他の子に関しては「長男」からprev、next等の「リンクを貼ってる」らしい。
また、各子は「親の情報」は持ってるが、親はあくまで「長男」しか知らん、と(笑)。なんか古い家柄みてぇだな(笑)。
いずれにせよ、「木」と言うよりはちょっとしたネットワークが構成されてるようになっている。
なお、GNodeはGTreeに比べると使用頻度は少ないらしく、ここでもアッサリと代表的関数を説明するだけ、でこの項を終わる事とする。
- g_node_new: 一引数関数。GNodeのコンストラクタで、引数に与えられた値をルートとしたGNodeを構築する。なお、引数はNULLでも構わない。
- g_node_append: マクロ。二引数。第一引数は親。第二引数はGNode。親に対しての末子を追加する(当然他に子がいなければ長男になる)。
- g_node_prepend: 二引数関数。第一引数は親、第二引数はGNode。それまでいた長男を廃嫡して(笑)、第二引数のGNodeを長男にする。返り値はGNode型。
- g_node_traverse: GNode用for_eachと考えておいていい。六引数手続き(プロシージャ)。第二引数でノードを辿る経路を指定できる。大雑把には深さ優先探索なのか、幅優先探索なのか、だが深さ優先では順序(In order)、事前順序(Pre order)、事後順序(Post order)を選ぶ事ができる。第三引数ではGNodeの何を辿るかが指定できる。第四引数ではGNodeを探索する「深さ」を指定でき、-1では全GNode、1でルートだけ、他の0以外の数値で「何段階」潜るか指定できる。第五引数はコールバック関数で、GNodeTraverseFuncの形式に従った関数が要り様。コールバック関数は真偽値を返し、真が返された時点でg_node_traverseは停止する。上の例だと関数iterがこのコールバック関数だ。第六引数はコールバック関数にGNodeと共に渡されるデータだが、特に必要がない場合はNULLを指定する。
- g_node_insert_data_before: 子の中で狙ったGNodeの前にデータを挿入するマクロ。第一引数は親、第二引数は狙った子、第三引数は挿入したデータとなる。
- g_node_reverse_children: 狙ったノードの子の順序を入れ替える下剋上手続き(プロシージャ)(笑)。長男が末っ子になり末っ子が長男になる(笑)。ただし、孫は影響を受けない。一引数。
- g_node_get_root: GNodeで構成された木のルート(根)を返す一引数関数。
- g_node_child_index: 指定されたGNodeの子の中から指定されたデータが何番目の子かを返す二引数関数。第一引数がノード、第二引数が第一引数の子の中から探したいデータ、となる。なお、データが存在しない場合-1を返す。
- g_node_destroy: GNodeで作られた木を破棄してメモリを開放する。ただし、木に使われたデータも含めて開放されるわけではない。