AVL Tree モジュール

プログラミングのアルゴリズムの話で、最初にこんがらがるのは木や二分木の話だ。

例えば初心者に説明するのに次のような図が使われる。

8を始点として6を検索してみる。

8は明らかに6じゃないので、8にある2つの子、3と10を見て小さい方の子、3へと進む。何故ならいずれにせよ、6は8より小さいから、だ。

3も明らかに6じゃないので、2つの子、1と6を見て、大きい方の6へと進む。

ここで6が得られたので、これでオシマイ、と。

このように、始点(根)やどの節の数より小さい数の集合は左の子に。逆に大きい数の集合は右の子に「まとまっている」のだが。

で、多分こんな風に考えるだろう。

「で?」

と(笑)。

いや、これは不自然な反応じゃない。よほどのボンクラじゃない限り理屈は理解出来るだろう。「その通りだ」と。

でも最初の印象は「だから何なんだ」なんだよな(笑)。確かに数値の構成見ればその通りにしかならないだろう。

問題は、だ。「だからこれが何に使えるんだ」って話になるんだよな。

ここで混乱する理由はハッキリしてる。単純な整数でのモデルしか出されてない、ってのが困る原因なんだ。

実は初心者向けの説明だと「キーとなる数値の探し方」しか示してないんで、ピンと来ないわけ。そう、初心者用の説明だと、知ってる限りどれ見てもこの「数値」のモデルしか出してないんで、全く何の役に立つんだか分からんわけだ。

実際は、例えば上で使われてる整数データと「検索したいデータ」を組み合わせて使うんだ。

Racketだったら例えばリストで

(1 'left 'right)

みたいな整数と欲しいデータと2つの子を組み合わせたデータ構造を作って、carをキーとした二分探索木を作るわけ。1を探せば欲しいデータである河北彩花の写真が検索出来る、と。

ちなみに河北彩花は例によってFANZAのAV女優ランキング1位のAV女優(2022年9月17日現在)だ。

今まで、Lispでの主要の検索用のデータ構造は連想リストとハッシュテーブルだった。

そして二分探索木、ってのは平たく言うと第三の検索用データ構造だ。ここで我々は3つ目の武器を手にする。

ハッシュテーブルは置いておいて、ここで連想リストを考えてみよう。

例えば次のような連想リストを作る。

(define *data*
　'((1 . )
　(3 . )
　(4 . )
　(6 . )
　(7 . )
　(8 . )
　(10 . )
　(13 . )
　(14 . )))

ちなみに、各写真はFANZA AV女優ランキング(2022年9月17日現在)での

1位: 河北彩花

3位: つぼみ

4位: 小花のん

6位: 日向かえで

7位: 小宵こなん

8位: 楪カレン

10位: 森沢かな

13位: 八蜜凛

14位: 東條なつ

と言う女性たちだ。彼女らをランキング順位通りにデータに置いてある。

んでだな。例えばassvで1を検索すると、

となる。そしてassvで14を検索すると、

となる。まぁ、当たり前だな。

ところで、assvなんかは次のような再帰コードで基本的には設計されている。

(define (assv key lst)
　(unless (null? lst)
　　(if (eqv? key (caar lst))
　　　(car lst)
　　　(assv key (cdr lst)))))

データとして与えられたリストの先頭の先頭を調べて、keyと一致してたらリストの先頭を返す。そうじゃなきゃリストのcdrを取って再帰、と。

んで、今どきのコンピュータは速いんで、あんま気にならんかもしれんけど、このコードを見れば分かるだろう。

データであるリストの先頭を探すような状態なら結果が返ってくるのは速い。しかし、データであるリストのケツに向かえば向かう程検索に時間がかかるんだ。

まぁ、この例のようにたかだか要素数が9個程度ならかかるコストは大した事はない。ただし、データが増えれば増えるほど検索コストが上昇するわけだ。

この検索コストの上昇を抑えたい、と言った要望に応える一つの方策が、二分探索木だ。平たく言うと、

「データの置き方を工夫すれば"平均的には"検索速度が向上すんじゃね?」

と言うのがアイディアだ。

Racketだと、同様のデータを次のように置いてみたら検索速度が上がる筈だ、と言う話だ。

(define *tree*
　'(8
　　(3 (1 #f #f)
　　　(6
　　　　(4 #f #f)
　　　　(7 #f #f)))
　(10 #f (14 (13 #f #f) #f))))

リストの要素を整数、写真、左、右とする。そしてそれぞれ適切な場所に入れ子にデータを組んでいく。

上の*tree*リストはまさしく二分探索木を形成している。

そして二分探索木自体が再帰的構造なので、木を辿る関数を書くのも実は簡単だ。根から子を辿って木は生成されてるが、節から子を辿っていってもそれは木構造になってるからだ。

例えば、上の写真で言うと根は「8」の楪カレンで、彼女から子を辿って木が生えてるが、部分的に、例えば3のつぼみから子を辿っててもやっぱり木になっている。

この辺に二分探索木のポイントがある。

この再帰的データ構造を活かせば、検索関数は単純には次のようになるだろう。

(define (tree-search tree value)
　(if (= value (car tree))
　　(cadr tree)
　　(if (< value (car tree))
　　　(when (third tree)
　　　　(tree-search (third tree) value))
　　　(when (fourth tree)
　　　　(tree-search (fourth tree) value)))))

上の二分探索木で言うと、1の河北彩花を検索する場合、まずは根の楪カレンの数値8とキーを比較して、同じ数じゃないんで、8よりも小さい数の集合である左に入って3のつぼみに合う。

3と1を比較しても同じ数じゃないんで、またもや小さい数の集合である左に入っていき、そこで1である河北彩花に出会えるわけだ。検索の再帰回数としては2回実行されてるわけだな。

一方、最初っから8の楪カレンを検索する場合、出会い頭に会えるわけだ。当然「検索コスト」としては楪カレンの方が河北彩花よりかからない。

ただし、二分探索木は、あくまで「平均で」検索コストがかからん、と言う事だ。

根は1個だがその子は最大2個、そのまた子は最大4個、そのまた子は最大8個、そのまた子は最大16個・・・とデータの枝分かれは倍増していき、データ総数は増える。その割には「検索関数の再帰回数」は増えないんだ。

例えば連想リストに32,767個のデータを詰め込むとする。データのケツにassvでアクセスするには文字通り3万回を超える再帰を行わないとならない。

一方、二分探索木なら再帰しても、最悪15回程度の再帰呼び出しで済む。3万回が15回に。二千分の一以上の圧縮率。

これは物凄く大きい、ってのは言わずとも分かるだろう。

以前、Racketで簡単なアドベンチャーゲームを書く例を紹介したが(1・2・3)、これは簡単な一枚のシナリオを実行するだけ、のゲームだった。

しかしADVにせよ、もっと複雑な、大量のシナリオだったらどうなるんだろう。

例えば以前紹介した Lone Wolfと言うゲームブック。最初の作品でさえパラグラフ数は300を超える。300だぞ?

いや、300を超えるのが「大きい」か「小さい」か、の判断は人によるが、さっき書いた通り、連想リストでシナリオを纏めたら、全部で350程の要素を持った大きさの連想リストだ。1番ならすぐアクセス出来るが350番目だとそうはイカン。350回くらい再帰を回さないと350番目に到達出来ない。

一方、二分探索木としてデータを構築すれば、最悪で9回、と言う再帰関数呼び出しで目的のパラグラフに到達する事が出来る。

つまり、二分探索木は充分ハッシュテーブルに対抗出来る素質を持ったデータ構造なんだ・・・・・・素質はな。

問題は、だ。上のFANZA AV女優ランキングの上位AV女優をRacketでまとめた二分探索木だが。手書きするのがクッソメンドイのだ。

こんなの人力で打つのは大変だ、って事に賛成する人ばっかだろう。俺だってそう思うわ(笑)。たった9個の節を持つ二分木でさえ書くのが大変なのだ。350もあったら発狂間違いなし、である。

そうなの。連想リストなら手作業でデータ構築するのは簡単だけど二分探索木はそうじゃない。

もちろん連想リストだって必ずしも人力でデータ構築するわけじゃない。ただし、手作業でデータ構築するのが簡単だ、と言う事は言い換えるとプログラムを書くのも簡単だ、って事だ。特に連想リストならSRFI-1にalist-consと言うデータ構築子が用意されてるんで、自動化する何かを書くのは晩飯後だ。つまり朝飯前だよな。

一方、二分探索木の場合、まるでプログラムがラクをするために人が苦労して書くようなデータ構造になってる。逆だろ。プログラムは人がラクする為のものじゃないか。じゃないなら本末転倒だ。

二分探索木が凄いのは分かった。問題はどうやったらそれをラクに使えるようになるのか、って話なのだ。

そうでもないと、単なる画餅で終わっちまうだろう。

ところでLispはヘンな言語である。いや、色々とヘンな言語なんだけどさ(笑)。

以前チラッと書いた事があるけど、そもそもLispのリストは万能、って言って良い。

従って原理的には他の言語のように「構造体を使って二分探索木を定義して・・・」って考えなくていい。上で見た通り、理論的にはリストで二分探索木なんてのは「面倒臭いにせよ」すぐ作れてしまうんだ。

LispはList Processorの略なんだけど、裏の面はTree Processorでもある。

しかし、それでもヘンなんだ。

例えばANSI Common Lisp。二分探索木だけに限らないんだけど、関数名をザーッと見ていくと、明らかに木構造操作を目的にしたような名前の関数がチラホラとある。それくらい木構造をイジる、ってのはANSI Common Lispにとっては重要なんだろう(そもそも、Lispプログラム自体が「構文木」そのものを弄くるようなスタイルになっている)。

ところが不思議な事に、木構造をイジる目的のような関数はあるんだけど、一方、木構造を自動で作る、と言うような関数はないんだよな。

これはホンマ不思議なの。連想リストを作るコンストラクタはある、ハッシュテーブルを作るコンストラクタはある、しかし木構造を作るコンストラクタはないんだ。

Schemeはもっと酷い。つまり、ANSI Common Lispは少なくとも木構造に言及してるような関数が仕様上定義されている。一方、Schemeは、SRFIをひっくり返して調べてみたんだけど、全く木構造に付いての言及がない。Schemerは木が嫌いなのか(笑)。

まぁ、ハッシュテーブルが便利だから実用的にはそれでいい、ってこたぁあるんだろうけどな。それでも不思議だ。なんせ何でもあるANSI Common Lispに存在しない、ってのはよっぽどの事だ。

実は僕が最初に二分木に遭遇したのは、いつぞや紹介した書籍、「これがLispだ!」だった。

この本でもまずは手書きで二分探索木を作る、と(笑)。上のAV女優木みたいなものを書くわけだよ。

「ええ、なんでこんなメンドイ事をせんとアカンの。簡単にこれ作れないの?」

と当時の僕も思ったんだよなぁ。Lispだと木を作る場合何でもかんでも手書きなのか、と(笑)。

「これがLispだ!」の結論では、二分探索木を連想リストで作ろうぜ、と言う結論になってる。「え?」とか言う結論だよなぁ。

つまり、上のAV女優木だと次のようなデータ構造にせよ、って事だ。

(define *psedo-tree*
　'((8 3 10)
　(3 1 6)
　(1 #f #f)
　(6 4 7)
　(4 #f #f)
　(7 #f #f)
　(10 #f 14)
　(14 13 #f)
　(13 #f #f)))

うん、まんま連想リストだ。違うのは通常使われるドットリストではなく(必須じゃない)、4要素のリストが要素になってる、って事だけだ。

この本の結論は、

「二分探索木作るくらいなら連想リストを使おうぜ」

と言う事で、次に検索するキーのヒントを要素のリストに含んでるだけで、あまり意味がないのだ。

と言うか、このスタイルだと、データの人力による追加・削除を重要視しただけで、実際問題二分探索木の旨味が全くない。

この結論で、僕個人は、連想リストの扱いには慣れたけど二分探索木の存在意義は全く掴めなかった、と言って良い。

そして、往年のLisperは木構造の自動作成は一体どうしてたんだろう?と言う謎を残したまま、ハッシュテーブルを愛用するようになったんだ。

と言う長い前ふりを終えて、本題に入ろう。

僕が夢見たような「自動で二分探索木を作ってデータを追加、削除出来るデータ構造」を平衡二分探索木と言う。そして何故に1987年出版の「これがLispだ!」にこの平衡二分探索木が紹介されてなかったのか。

一番あり得る話としてはこの時点で、平衡二分探索木がメジャーじゃなかったと言う事が考えられる。分からんけどな。

と言うのもWikipediaに拠ると、平衡二分探索木の発展の歴史ってのは次のようになっている。

一番最初に現れた平衡二分探索木と言うのは1962年に出てきたAVL木、と言われるモノだ。開発者はГео́ргий Макси́мович Адельсо́н-Ве́льскийとЕвге́ний Миха́йлович Ла́ндисの二人。

名前見れば分かる?そう、今は無きソビエト連邦の科学者なんだわ。

つまり、分からんけど、当時ソビエトで開発された技術ってのはその時点では西側に入ってきてない可能性があるわけ。

だからまずこれが平衡二分探索木が最初に広まらなかった原因じゃないか、って思ってる。

次に出てくるのが赤黒木ってヤツだな。

赤黒木の例(違

赤黒木の開発者はドイツ人。1972年のこの時点でも、コンピュータのメッカ、アメリカでは、少なくともWikipedia(日本語版)では、平衡二分探索木の開発者が出てきてないんだ。

1985年のスプレー木でやっとアメリカ人計算機学者の開発者が出てくる。「これがLispだ!」の原著が出版される二年前だ。そしてこれが皮切りとなってアメリカ人計算機学者の仕事が増えてくる。

いや、これが事実かどうかは知らんよ。でも、Wikipediaでまとめられてる記述から類推する以上、平衡二分探索木って(西側に取っては)結構新しい技術で、普遍化したのは1990年代以降なんじゃないか、って事。そうすれば「これがLispだ!」やANSI Common Lispで取り扱われてない理由になるんじゃないか、って思う。

知らんけどよ。

とまぁ、お立ち会い。

Racketの外部ライブラリに、このうち、AVL木を取り扱えるモノがある。

「今までAV女優の写真使ってたのはAVL木を取り扱う為だったのか!」

と思ったアナタ。やかましいわ!(笑)。

オホン、RacketでAVL木を取り扱える外部ライブラリの名前をAVL Treeモジュールと言う。

外部ライブラリである以上、Racketの標準ではない。

しかし、RacketにもPythonで言うトコのpipっぽいものがある。それがracoだ。

厳密に言うと、元々racoはRacketのコンパイラだった。しかし、今やネットワークを介したライブラリのインストールツールとしての機能も持っている。結果、ネット経由でインストールした外部ライブラリは無事、Racket用にコンパイルされて使用可能となる。

AVL Treeモジュールのインストールは、端末から

raco pkg install avl

で行える。このコマンドを走らせた後ならAVL木が使い放題となる。

当然、AVL木を使う場合、ソースコードに

(require avl)

と記述する。

さて、平衡二分探索木とは何か。詳しい事はWikipediaに記述してあるのでそれを読んで欲しいが、平たく言うと、二分木の「構築しづらさ」を解決するメカニズムだ。

上の方で行ったリストで作った二分木をもう一度見て欲しい。

(define *tree*
　'(8
　　(3 (1 #f #f)
　　　(6
　　　　(4 #f #f)
　　　　(7 #f #f)))
　(10 #f (14 (13 #f #f) #f))))

これを手で作るのは大変だ。

ついでに言うと、手で作るのが大変だ、と言う事はデータの追加や削除が大変であり、また、根をどのデータにするのか、節をどう選んでいくのか、と言う「手順」も全て大変だ、と言う事になる。

しかも、歪な木を構成すると、二分探索木にある筈の「検索に対する高効率性」も画餅になってしまう。

平衡二分探索木は、これらの諸問題を「自動で」解決してくれる技術だ。

AVL Treeモジュールでまず必要な関数は次の「ALV木生成関数」だ。

この前に3つ程別のAVL木生成関数が紹介されているが正直役に立たない。

と言うのも、それら3つのAVL木生成関数は、単項のデータを作る程度にしか使えないんだ。今まで見てきたようなAV女優木みたいなキーと参照したいデータが合わさってるカタチだとmake-custom-avl関数を使った方がいい。

make-custom-avl関数は比較関数と等価判定を自作して与える。上の図の例だとラムダ式を使って「データのどの部分を使って比較するか」指定してる。

次に覚えるべき関数はデータ追加関数だ。

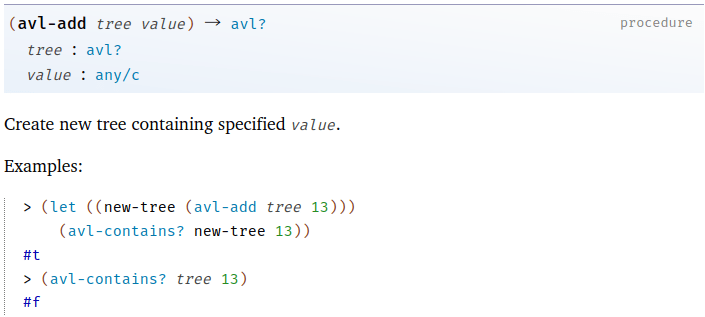
破壊的変更版も存在するが、我々のような関数型言語マニアはそっちは使わない。

先程のAVL木生成関数とデータ追加関数の2つがあれば、連想リストをAVL木に変換する関数は簡単に書ける。

(define (alist->avl alist)
　(foldl (lambda (value tree)
　　　　(avl-add tree value))
　　　(make-custom-avl (lambda (x y) (<= (car x) (car y)))
　　　　　　　　　　　(lambda (x y) (= (car x) (car y))))
　　　alist))

AV女優ランキングの連想リスト*data*をAVL木に変換してみよう。

変換された*av-tree*と言うAVL木は、オーソドックスに構造体になっている。

最後に重要な関数は、当然検索関数になる。

この関数はちとクセがある。

と言うより、make-custom-avlの比較関数が「データのどの部分で比較してるのか」指定してるので、その指定形式を使わないとエラーになってしまうんだ。

*av-tree*はcar部分で比較した。だから与えるキーがリストでないとならない、と言う制限が生じるんだな。

例えば*av-tree*からcarが1のデータを探したい場合にはキーに1ではなく、'(1)と言うリストを与える。そうすれば'(1)のcarである1が使われて、検索が性交成功する。

同様に*av-tree*からcarが8のデータを探したい場合には'(8)を与えるわけだ。

正直言うと、ちと設計が下手クソだよな、と思う。

従って、上の図のように、キーをそのまま与えるように改造した方が使い勝手はいいと思う。

(define (search-by-key tree key)
　(avl-search tree `(,key)))

そうすれば、連想リストのように検索が可能となるだろう。

あとは、削除関数を覚えておけば基本的には良い筈だ。

ただ、関数型言語マニア的には、リアルタイムでの木の更新よりプログラムをスタートした後で永続的に使えるデータ構造としての探索二分木に興味がある。要するに「如何にデータを保持するか」だ。

結果、それほど、プログラムを動かしてる間の「データ変更」には興味がない。

よって最低でもこの4つの関数を、プログラムの「立ち上げ時」に使えば当面は問題が無い筈だ。

さて、平衡探索二分木を見てきたが、一方、キーに数値しか使えないんだろうか、とちと疑問に思う向きもあるかもしんない。

しかし別に数値に限る必要はない。いつぞや見た通り、文字列で大小が定義出来るのなら辞書順で平衡探索二分木が定義出来る。

例えば次のような連想リストを作ってみよう。

(define *av-list*
　'(("河北彩花" . )
　("つぼみ" . )
　("小花のん" . )
　("日向かえで" . )
　("小宵こなん" . )
　("楪カレン" . )
　("森沢かな" . )
　("八蜜凛" . )
　("東條なつ" . )))

そして次のような変換関数を書く。

(define (alist->avl alist)
　(foldl (lambda (value tree)
　　　　　(avl-add tree value))
　　　　(make-custom-avl (lambda (x y) (string<=? (car x) (car y)))
　　　　　　　　　　　　　(lambda (x y) (string=? (car x) (car y))))
　　　　alist))

まぁ、比較関数と等価判定を文字列用に取っ替えただけだが、Racketのキーワードを使えばもっと一般化出来るかもしんない。

(define (alist->avl alist (cmp <) (eq equal?) #:keyword (fn identity))
　(foldl (lambda (value tree)
　　　　　(avl-add tree value))
　　　　(make-custom-avl (lambda (x y) (cmp (fn x) (fn y)))
　　　　　　　　　　　　　(lambda (x y) (eq (fn x) (fn y))))
　　　　alist))

いずれにせよ、連想リストをAVL木に変換して、