博士の愛した数式とGoogleの電卓機能

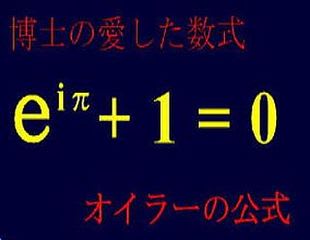
これは映画「博士の愛した数式」で有名になった「オイラーの等式」である。ネピア数（自然対数の底）のべき乗のところに「iπ」という虚数を代入して１を加えると答えがゼロに等しくなる。べき乗というのは2の2乗=4のように右上の指数のところに書いた数字のぶんだけ掛け算するという意味だから、π乗するというのは「e(=2.71828...)を3.14回掛ける」ことになるわけで、答えは3回掛けたときと4回掛けたときの間なのだろうと想像できる。

実際にGoogleの電卓機能を使って計算してみると

e^3 = 20.0855369
e^π = 23.1406926
e^4 = 54.59815

となり、予想は正しいことがわかる。（リンクをクリックするとGoogle電卓で実行した結果が表示される。）

eのiπ乗のほうはもっとイメージしにくい。つまりiというのは虚数で「２回掛けると-1になる数」なわけだから、「eという実数値(2.71828...)を3.14...の虚数回掛ける」ことになるからだ。Google電卓に頼ってみよう。

e^(π * i) = -1

答えは-1という実数値に。。。。右辺の-1を左辺に移項するとおなじみの「博士が愛した数式」になる。

(e^(i * π)) + 1 = 0

Google電卓ってすごいな。。。。

この「オイラーの等式」は「オイラーの公式」(e^ix = cos(x) + i*sin(x) )のxにπを代入したものだ。(オイラーの公式の証明はこちら。)この公式は指数関数と三角関数、虚数の間の不思議な関係を示していて、アインシュタイン以降の現代物理学に欠くことのできない法則である。それどころか虚数やオイラーの公式を認めないと身の回りのあらゆる電子機器やレーザー光線、超伝導の原理が成り立たないばかりか、物が固いおかげで人間が地面の上に立っていられることすらも説明がつかなくなってしまうのだ。

物を投げるときに描かれる軌跡は放物線であり２次関数であらわされるが、それと同じくらいの確からしさで虚数やオイラーの公式を認めなければならない。虚数というものが人為的に仮定した単なる想像上の数(=想像上の世界)ではなく、実数(=現実の世界)と同じくらいの（もしかするとそれ以上の）実在感を持っていることを示している。このことについてはまた今度書くことにしよう。

ちなみにオイラーの等式のπ（3.14...）からちょっとずらして3.15を入れてみると右辺の答えはゼロにはならず、ゼロのすぐ近くの複素数になる。

(e^(i * 3.15)) + 1 = 3.53415287 × 10^(-5) - 0.00840724737 i

お遊びついでに「eのi乗(e^i)」や「iのi乗(i^i)」はどうなるかといえば、それぞれリンクのところをクリックしてみてほしい。

虚数、複素数関連の記事：

虚数の情緒
http://blog.goo.ne.jp/ktonegaw/e/27155c8d7b5242d7e69e00335411acc1

オイラーの贈物
http://blog.goo.ne.jp/ktonegaw/e/fd87442dfc1b3dc7561fb5fdd72bff13

数学の神秘
http://blog.goo.ne.jp/ktonegaw/e/f5879a6b87bb05ddfac16927785ef435

複素関数
http://blog.goo.ne.jp/ktonegaw/e/de895908dc5ec348ed677346fa37e840

因数分解（複素数）
http://blog.goo.ne.jp/ktonegaw/e/e54dfcd47b72ae247a22206c05bfaa8e


ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。