
「カオス的世界像―非定形の理論から複雑系の科学へ: イアン・スチュアート」
内容紹介:
神はサイコロ遊びをするか?現代科学が抱える難問の核心にあるカオスの正体に迫る。
近年広い分野で興味を持たれているカオスに関連した自然現象を、ほとんど数式を用いずにわかりやすく説明し、豊富な例え話とともに複雑な理論へ導いていく。1992年刊(382ページ)のものに新たに4章を加えた増補新版。
1998年10月刊行、519ページ。
著者について:
イアン・スチュアート(Ian Stewart)
ウォーリック大学数学部教授。英国の第一線の数学者であり、ポピュラーサイエンス書の著者としても世界的に有名。2001年に、王立協会のフェローとなる。新聞や雑誌の記事の執筆、テレビの科学番組への出演なども積極的に行っている。著書に、『数学の秘密の本棚』『世界を変えた17の方程式』『数学で生命の謎を解く』(いずれもSBクリエイティブ)、『もっとも美しい対称性』(日経BP社)、『自然界の秘められたデザイン』(河出書房新社)などがある。
イアン・スチュアートの著書日本語版: 単行本検索 Kindle版検索
イアン・スチュアートの著書英語版: ペーパーバック検索 Kindle版検索
理数系書籍のレビュー記事は本書で436冊目。
とにかく読み応えがあり、知的興奮を与えてくれた科学教養書である。フランスの数学者アンリ・ポアンカレが20世紀初頭に(後にカオスと呼ばれるようになる)不規則な天体の軌道の有り様に気づいて以来、このカオス理論と呼ばれる数学は、さまざまな道具とアイデアを駆使して発展してきた。特に1960年代以降、コンピュータが利用され始め、1970年代以降にコンピュータ・グラフィックスが利用できるようになり、カオスは目に見える形で姿をあらわし、研究に拍車がかかった。
カオスとは一般用語では「混沌」という意味だ。自然現象や人間が営む社会活動、経済活動、そして変化するあらゆるものには、不規則で取り扱いが難しいものが多い。そのうちのいくつかは、確率的、統計的に扱うことで平均的なふるまいを把握することができる。完全にランダムでその挙動が予測できない現象も、たとえば気象予報のようにコンピュータで取り扱うことができるものがある。カオス理論の起源は天体力学だが、適用できる対象は「およそ不規則に変化するあらゆる領域」にまで広がっている。
しかし、カオス理論が扱う対象は、確率や統計学的に見られる「平均値化」とは相入れない不規則な動きをもっている。将来の動きが予測できないのだ。とはいってもまったくランダムということではなく、不規則性の中に一定の秩序や数値であらわされる法則や性質をその中に見つけることができる。そのために、人間の目からはまったく異なるカオス現象であっても、共通した手法でアプローチすることができるようになるのだ。
また、混沌の中に秩序があることがわかると、その不規則な挙動に影響を加えることで、そのカオス的挙動を利用して人間の生活に役立てることができる場合がある。「カオス制御」と呼ばれる新しい工学分野は、すでに医療分野で利用し始めただけでなく、宇宙船に対してカオス的軌道を利用することで、より燃料効率のよい形で目的地の天体まで到達させることができるようになると予想されている。
本書はまた、カオス理論の発展史を知る上でも、最良の本だと思われる。言葉を尽くして具体的に詳細を語ることで、読者にとって読みやすい本となっている。質の良さはさることながら、ページ数が多いのはそのためだ。
章立てはこのとおりである。
プロローグ:時計仕掛けかそれともカオスか?
1 秩序から混沌へ
2 万能方程式を求めて
3 誤差の法則
4 最後の普遍学者
5 単方向振子
6 ストレンジ・アトラクター
7 お天気工場
8 カオスの調理法
9 センシティブ・カオス
10 フィッグ・ツリーとファイゲンヴァリュー
11 ほんものそっくりの感触
12 再びヒペリオンについて
13 自然界の不均衡
14 バタフライを超えて
15 フォン・ノイマンの夢
16 カオスと量子
17 深遠なる思考よ、さらば
結語:神とサイコロ遊びを...
プロローグ:時計仕掛けかそれともカオスか?
この世界はニュートンが予言するように時計仕掛けなのか、それともアインシュタインが言及したように「神はサイコロを振らない」のか、それとも「振る」のか?現代物理学は「振る」ほうに軍配を上げていて、それでは「神はどのようにサイコロを振るのか?」という問いに答えるまでになっている。そこに至る過程で測定、予測可能性、理論の実証、それに対する反証など新たな疑問が生じてくる。そのかわりに、複雑に見えるものが単純なものになってしまうこともあるし、逆に、一定の構造をもたず、でたらめに見える現象も実際には単純な法則に従っているかもしれない。決定論カオスは、それ自身の法則をもち、新たな実験技術に対して指示を与える。自然界の現象は非常に多様であり、それらのあるものは、カオスの数学の物理的対応物でありうる。液体の乱流、地磁気の逆転、心臓の鼓動の不規則性、液体ヘリウムの対流パターン、天体の回転、小惑星帯の空隙、昆虫の個体数の増加、水道の蛇口から出るしずく、化学反応の進行、細胞の新陳代謝、天候の移り変わり、神経パルスの伝播、電子回路の振動現象、ブイに係留してある船の振動、ビリヤードボールの跳ね返り、気体原子の衝突、量子力学の根底にある不確定性。--- これらは、カオスの数学がこれまで扱ってきた問題のいくつかの例である。
1 秩序から混沌へ
ニュートンからラプラスまでの力学の歴史を解説し、この世界は時計仕掛けのように未来が決まっているのか?それとも確率的にしか予測できないのかについて考察を進める。また、そのどちらでもない不規則な現象が存在していることを、いくつかの例を取りあげて紹介する。ヒペリオンという惑星が見せる不規則な挙動、電卓で反復計算する際にあらわれるカオスなどである。
2 万能方程式を求めて
古代の天文学、アンティキティラと呼ばれる古代ギリシャの惑星軌道計算機、コペルニクスからニュートンの宇宙観に基づく宇宙観の歴史、オイラーからフーリエ、ラグランジュ、ハミルトンに至る解析学史、決定論的には解くことのできない現代のさまざまな問題が紹介される。
3 誤差の法則
確率論、統計学の歴史を解説し、その中で確率分布、誤差や平均はどのように現実の対象を結びついているかを論じる。多数の集団を扱う統計力学が解説される。また、その中に見られるランダム性は、実はランダムではなかったということに気づき、それは「必要な情報が不足している」ことによる見かけのランダム性であったと解釈された。また、19世紀末までに科学は数学モデルの構築に対して2つのパラダイムを獲得していた。昔からあった決定論的な微分方程式を利用する解析学、そしてもうひとつは高度に複雑なシステムにおける運動を、平均という大ざっぱな特徴を表現する統計解析であった。そして、ほとんどの科学者は単純な決定論的系がランダムな系に似た振る舞いをするということに否定的だった。
4 最後の普遍学者
アンリ・ポアンカレの登場である。彼の片方の足は19世紀に、そしてもう片方の足は20世紀に置いた格好で両足を広げ、数学史の転換点にそびえるがごとく立っていた。彼の功績のひとつは、力学系における定性的理論の基礎を築いたことである。ポアンカレには学問的な懐の深さはあったが、天体の複雑極まりない軌道を照らし出す道具は持ち合わせていなかった。このカオスの深淵に光を当てて、その美しさを照らし出すためには、コンピュータや、その関連技術の助けが必要だった。したがってポアンカレは微分方程式にもとづく定性的な理論で武装したのである。その過程で彼が利用したのがトポロジーだった。ホモクリニック軌道、ヘテロクリニック軌道は、トポロジーに対して新たに導入した「ポアンカレ断面」というアイデアによって発見された。(参照:「ポアンカレ 常微分方程式 -天体力学の新しい方法-」、「ポアンカレによるカオスの発見と先見性」)
5 単方向振子
解析的な手法では解くことができない、非線形振子の問題が取り上げられる。この問題はトポロジーの幾何学の表現に映され、「エネルギー」という視点から解く方法が発見された。そしてこの抽象空間を利用した解法は多次元化され、幾何学の多次元かが進んでいくのである。
6 ストレンジ・アトラクター
微分方程式の解の安定性についての解説が始まる。 シンク[吸い込み口]、ソース[湧き出し口]、サドル[鞍部]、リミットサイクル[極限周期軌道]など、相空間に描かれる対象、基本的な用語を図を使って説明する。そして準周期的運動の表現に必要になる形がトーラスである。この章ではまた、スメールの研究が解説される他、カオス理論に新しく追加された構造安定性、アトラクター、巻き込み写像、カントール写像などが紹介、解説される。
7 お天気工場
天気の数値予報がこの章のテーマである。大気という連続体を離散的に取り扱って計算するのが数値予報である。カオス理論はその初期値鋭敏性という性質により、観測精度をどんなに上げても、コンピュータの性能をどんなに上げても完全に天気を予測することはできない。また、初期値鋭敏性は「バタフライ効果」として知られる現象をもたらす。バタフライ効果が実際におこっていることは、計算によりすでに確認されているのだ。気象の数値予報の研究を進める中で1963年に発見されたのが、「ローレンツ・アトラクター」である。
8 カオスの調理法
カオスの研究手法として考案された「スメールの馬蹄写像」、「ロジスティック写像」が解説される。そしてロジスティック写像の中に「周期倍増型カスケード」と名付けられたカオスがあらわれていることを確認する。つまり、カオスの中に秩序が存在することが発見されたのである。この章はカオス理論の1940年代から1970年代の研究を解説した章だ。
9 センシティブ・カオス
水の流れをテーマに、カオスの奥深さが語られる。水道の蛇口から落ちる水滴は、蛇口をひねるにつれて一定間隔リズムで、次に不規則なリズムになり、層流から乱流へと変化する。この過程で2回の状態遷移がおきているのだ。また、回転する車輪で生じる振動(ウォッブル)、流体力学で見られる乱流がカオスであることが紹介される。その解明のために考案されたアイデア、数学的手法が紹介される。この章で重要な概念として解説されるのがカオス振動の「パワー・スペクトル」である。また、時系列に沿った振動の観測量は1次元である。この系列をシフトして3つの系列にして、3次元の図形としてアトラクターを構成する「パッカード-ターケンス法」という手法が紹介される。この手法によって1986年、したたり落ちる水道水の水滴からアトラクターの再構築に成功した。つまり不規則に見える水滴のしたたりには秩序があったのである。また「レスラー・アトラクター」が紹介されるのもこの章だ。
10 フィッグ・ツリーとファイゲンヴァリュー
1970年代半ばのファイゲンバウムによるウィルソンのくりこみ法を乱流に応用する研究がこの章で紹介される。キーワードはフィッグ・ツリーとファイゲンバリューだ。手始めにロジスティック写像から始めた。当時利用できたHP-65というプログラム電卓を利用して数値の反復計算を行なったのである。その後継機であるHP-67はスマホアプリとして入手できるし、プログラムは単純なので、どうせならこの機種を使ってご自身で試されるとよいだろう。(もちろん他のプログラム電卓でも構わない。ちなみにCASIO高精度計算サイトのこのページでも計算することができる。) そしてこの章で重要なことは、ファイゲンバリューなどカオスを判定するための定量的な値が存在することが発見されたということである。
11 ほんものそっくりの感触
海岸線のギザギザな形は、その部分を拡大すると、似たようなギザギザがあらわれる。自己相似形であるといってよい。この章で紹介されるのは「フラクタル」である。そして整数値をとらないフラクタル次元が解説される。またフラクタルもカオス理論にとって欠かすことができない。フラクタル次元数を測定することで、カオスの判定に使えること、乱流に対するフラクタルとカオスとう2つのアプローチは「姉妹」であることが発見される。つまり、ストレンジ・アトラクターはフラクタルだったのである。この章では「マンデルブロ集合」、「ジュリア集合」が紹介される。ただし、乱流がフラクタルであるとするのは早急だ。また、フラクタルを利用した画像圧縮技術も紹介される。
12 再びヒペリオンについて
カオス的な回転をする土星の衛星「ヒペリオン」のメカニズムが詳しく解説される。また、衛星や惑星、小惑星の公転がもたらす共鳴現象を解説する。共鳴は(エネルギー保存系の力学である)ハミルトン系の力学において特に重要で、カオスはしばしばそれらの共鳴現象として生じることが多い。共鳴現象は、また小惑星帯の空隙(ギャップ)の謎も解明した。そもそも太陽系全体は本質的にはカオス的であることが示される。
13 自然界の不均衡
生態系における動物の個体数がカオス的に変化することを紹介する。生態学(エコロジー)に関する一般的な書物や、あるいは環境保護団体からきた寄付集めの手紙を見ると、それほど読み進まないうちに「自然界の均衡」という言葉に出会う。つまり、すべての種は、人間たちによっていとも簡単に壊されてしまうような、非常にデリケートな「生命の編目」で結びつけられているとかのおとぎ話が書いてあるのだ。この種の議論にはおかしなところがたくさんある。定常状態といえども、そのまま衰弱するのではなく移動してカオスにより、安定性の破壊が生じることもある。アトラクターの概念は、このような問題にも自然かつ有用なイメージを与えてくれる。多くの人々は単純明快な答を求めるし、またほとんどの政治家たちや圧力団体は単純明快なスローガンを求める。生態系はこのような人々にとってはあまりに複雑すぎるのだ。カオス理論は、このような複雑性がもたらす問題を解決してくれるのではなく、むしろ、そのような問題があることをわれわれに認識させてくれるのである。またこの章ではカオス理論の研究がHIVウィルスや心不全など脈動する臓器の研究にも有用であることを紹介している。
14 バタフライを超えて
ランダムであることとカオスはどのように違うのかを、とても詳しく解説する。そしてそれらの違いが、現実世界における予測とどのように結びついているか、どのように応用されているかが紹介される。そして、最後にバネの製造の例をとりあげ、その歩留まりを抑え、不良な製品をどのようにして減らすことができたかという、カオス理論の工業的な応用例が紹介される。
15 フォン・ノイマンの夢
1950年頃、偉大な数学者ジョン・フォン・ノイマンは微小擾乱(バタフライ効果)に対する天候の敏感性についてはじめて耳にしたとき「天候は予測不可能ではない。それは制御できる。」と述べたそうだ。将来、優れた計算機を持つようになったら、たちまち気象現象を2つの範疇にはっきりと仕訳できるようになるだろう。安定なものと不安定なものに。そして安定なすべてのプロセスをわれわれは予測できるであろう。また不安定なすべてのプロセスをわれわれは制御できるだろう。」つまり、天候にちょっと干渉するだけで大きな効果を及ぼせるのはもうわかっているのだから、どんなに大きな効果でも望みどおりに引き起こす経済的な方法が存在するはずである。カオス制御の話だ。
ここまで読んだとき、僕は昨年の台風15号、19号による豪雨被害のことを思わずにはいられなかった。事前に予測できていれば、わずかの影響を大気に与えるだけで、数日後の台風の進路や豪雨域を海上にそらすことができたかもしれない。現在は無理だが、将来そのような技術が実現することを切に願っている。
また先日、この連続投稿がツイッターでバズった。(連続投稿を開く)
三体問題のカオス的軌道を採用することで、それまで最も効率的と考えられてきたホーマン軌道を採用する場合の半分の燃料で宇宙船を月の周回軌道に乗せることができる。ただし地球を48周、月を10周回るため2年かかるが、将来月面基地建設のための物資を運搬するためには効率的だ。
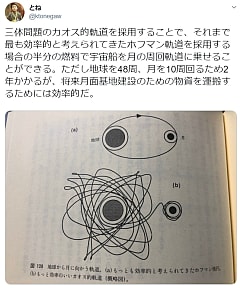
フォロワーや読者の中には「カオスの初期値鋭敏性があるから、このようなことは不可能だ」と主張する方がいたが、実はそうでもない。月に到着する直前で軌道がぐにゃりと曲がっている場所がある。これは慣性に任せたカオス的軌道ではなく逆噴射して軌道修正したことによる。つまり、その場所まではカオス的軌道に任せ、最後の最後で燃料を使っているのである。また、途中で燃料をわずかに使って軌道を微修正することも可能である。このようにすればホーマン軌道の半分の燃料で済むのだ。
また、この章では脳波の研究にカオス理論のアトラクターが使われていることも紹介される。
16 カオスと量子
量子力学の不確定性原理も予測を不可能にする原因である。カオスのそれとどのように関連付けて考えればよいのだろうか?この章では、量子力学の発展史を解説した後に、まだ解明されていないこの領域の考察を深めている。
17 深遠なる思考よ、さらば
最終章は、複雑系と呼ばれる分野の解説だ。カオス理論が「単純な規則から不規則性が生まれる」ことであるのに対して複雑系は逆である。本書が刊行された頃に注目されてきたのが複雑系である。これについては、簡単に述べるにとどめ、本書の後に続編として刊行した「The Collapse of Chaos(カオスの崩壊)」で詳しく解説をするとしている。
また、この章では理論物理学者の多くが信じている「要素還元主義」について紹介している。素粒子の挙動がすべての自然現象の根源にあるとするこおの思想は、古代ギリシャからあった考え方だ。しかし、現実の問題はスケールに応じて別々の理論で理解され、それらの間に存在するギャップは大きく、それを埋めることはほぼ不可能な状況である。そのことを象徴的に示しているのが「ラングトンの蟻」という不思議なカオス現象である。この現象については、ここから始まる連投ツイートで紹介しておいた。色の数を増やしたもの、3Dバージョンにしたものなど、不思議で美しい動画が見れるので、ぜひご覧いただきたい。
ラングトンの蟻(解説動画)
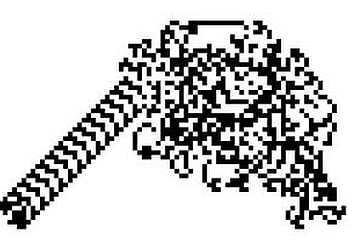
ラングトンの蟻(2D多色版+解説動画、3D多色版動画)
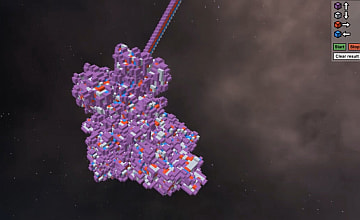
ラングトンの蟻の不思議は数学的に解決されていない。不規則なカオス的挙動から、なぜ突然「道」が作られ始められるのか?蟻の運動を決める規則はごく単純なものなのだ。この謎は解明されていないし、数学的に証明もされていない。何が解明されていないかは、このスライドに書かれている。
ツイッターでアンケートをとってみたところ、114人の方から回答をいただき、92.1パーセントの方が「ラングトンの蟻」をご存知ないという結果になった。(アンケートを見てみる)
ラングトンの蟻でできる「道」や「規則的な幾何学図形」は、このカオス現象におけるアトラクターである。これを観たとき僕は、将棋で互いに最善手で指すうちに偶発的に生じる「千日手」のようなものではないかと思った。千日手では同じパターンの指し方が無限に繰り返されるからだ。
ざっと本書の内容を章別に紹介させていただいた。絶版なので安い中古本を見つけることができたら、ぜひお読みいただきたい。
日本語版は新版と旧版が販売されている。できれば新しいほうを買ってほしい。
「カオス的世界像―非定形の理論から複雑系の科学へ: イアン・スチュアート」(1998年、増補新版、519ページ)
「カオス的世界像―神はサイコロ遊びをするか?: イアン・スチュアート」(1992年、初版、382ページ)


増補新版の検索: Amazon 日本の古本屋 ヤフオク メルカリ
増補新版の翻訳のもとになった原書はこちら。Kindle版は安く買える。
「Does God Play Dice?: The Mathematics of Chaos: Ian Stewart」(Kindle版)

本書の続編は「The Collapse of Chaos(カオスの崩壊)」というタイトルで1994年に刊行された。
「The Collapse of Chaos: Discovering Simplicity in a Complex World: Ian Stewart」(Kindle版)

そして同じ著者が「神はサイコロ遊びをするか?」ではなく「サイコロは神遊びをするか?」という本を書いていることに気がついた。Kindle版はすでに発売され、ペーパーバック版は6月、ハードカバー版は9月に発売される。
「Do Dice Play God?: The Mathematics of Uncertainty: Ian Stewart」(Kindle版)

関連記事:
ポアンカレ 常微分方程式 -天体力学の新しい方法-
https://blog.goo.ne.jp/ktonegaw/e/8dc81ef7e48c812b56befcc2345d59d4
天体力学のパイオニアたち 上: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/5c51d50e2141c8ae58c9323ad49b65a1
天体力学のパイオニアたち 下: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/88846fbb12ed1f8b11a49f0659b93c75
数理解析のパイオニアたち: V.I.アーノルド
https://blog.goo.ne.jp/ktonegaw/e/165c894d023b1174fd519522935cdeeb
Hirsch・Smale・Devaney 力学系入門 ―微分方程式からカオスまで― 第3版
https://blog.goo.ne.jp/ktonegaw/e/98d451af90b7efc63aacbe4efdb330fa
力学系カオス: 松葉育雄
https://blog.goo.ne.jp/ktonegaw/e/12392ac282d10deed28914d8182c2286
「磁石振り子」によって現れるカオス軌道とフラクタル図形
https://blog.goo.ne.jp/ktonegaw/e/d47ee62678af4791420f81c70ef8002f
メルマガを書いています。(目次一覧)

応援クリックをお願いします。







「カオス的世界像―非定形の理論から複雑系の科学へ: イアン・スチュアート」

増補新版への序文
プロローグ:時計仕掛けかそれともカオスか?
1 秩序から混沌へ
- 不条理な論証
- 時計仕掛けの世界
- ヒペリオンへの旅
- カオス
- 電卓カオス
- ヒンズー教におけるメンテナンスの技法
2 万能方程式を求めて
- 天球の回転
- ギリシャで生まれた歯車
- 太陽中心説
- 振子の運動
- 重力(万有引力)と幾何学
- 世界の体系
- 鐘と笛
- 風と波
- 解析学が見捨ててきたもの
- 質入れされた数学
- 再定式化の時代
- 市場は大騒ぎ
3 誤差の法則
- ギャンブルで勝ちたい!
- 並の人、または「平均人」という概念
- 遺伝研究の天才=形質遺伝と正規分布
- テクノロジー・トランスファー
- オランダ生まれのカオス
- パラダイムを延命する
4 最後の普遍学者
- うっかり屋の空想家
- 数学のオスカー
- ラバーシート・ダイナミックス
- 四方八方めったらやたらに大突進
- 三角関係のもつれ
- トポロジーへの一つの疑問
- 天上のカオス
5 単方向振子
- 勝てないときはずるをする
- エネルギー曲面上の幾何学
- 非ゾウ学
- 円に線を巻きつけて
- 事実は摩擦より奇なり
- 多次元の夢
- n次元空間における幾何学
6 ストレンジ・アトラクター
- 光陰矢の如し
- シンク[吸い込み口]
- ソース[湧き出し口]
- サドル[鞍部]
- リミットサイクル[極限周期軌道]
- 典型的にはまさにこれ
- 猫を振りまわして
- 日に映る景色ではなく精神に映る景色
- 構造的安定性
- アトラクター
- 巻き込み写像
- カオスの足跡
- ポアンカレ断面
- 宙ぶらりんのソレノイド
- カントールのチーズ
- ほんもののカオス
- 痛烈なこきおろし
7 お天気工場
- 輝かしき失敗
- お天気チェス
- 0と無限大の間で
- メガフロップ
- 心の中は数学者
- 滞留せずに対流に挑む
- コンピュータのおかげです
- バタフライ効果
- その蝶をたたき落とせ
- 引き延ばしと折りたたみ
8 カオスの調理法
- 引き延ばしと折りたたみ
- レーダーから馬蹄まで
- ディナミックス・ボロニェーズ
- 磁気トラップ
- パフ・ペイストリー
- ミセス・ビートンを越えて
- ロジスティック写像
- 定常状態レジーム
- 周期倍増型カスケード
- カオスの中にある秩序
- 大きなノミ、小さなノミ
9 センシティブ・カオス
- 奥の深さを見抜くには
- ウォッブルが雪だるま式に
- ありそうもない筋書き
- 反証可能性
- 古典的室内実験
- レーザー光の照射
- 出会いと接点
- でっちあげの観測可能量
- ストレンジ・ケミストリー=化学反応の不思議
- 芭蕉再訪
10 フィッグ・ツリーとファイゲンヴァリュー
- 宇宙の大海原に漂う一本の壜
- 摂動はダメ、くりこみだ!
- 大型汎用コンピュータを使わない利点
- 蛇と熊
- くりこみ法
- ファイゲンバウムの写像
- ファイゲンバリュー
- 両刃の剣
- 空想の世界で乱流を見る
- 極寒と静寂の世界
- ヘリウムの回転運動
11 ほんものそっくりの感触
- 測定の尺度
- 雪片と海岸線の形
- 1 1/4 次元
- 「幾何学だけはやらないほうが...」
- シリコン・バレー
- 凝集と浸透
- 水と油はどうして混ざり合わないか?
- 万物と宇宙
- フラクタル偽造物
- 雲と雨
- 実は姉妹だった!
- ジンジャーブレッド・マン
- フラクタルの牛
12 再びヒペリオンについて
- 宇宙のじゃがいも
- バンパイヤ・ドッペルゲンガー
- スピン軌道の幾何学
- 潮汐摩擦
- どうして、そういうことになったのか?
- 共鳴現象
- カーターウッドのすきまとヒルダのかたまり
- 高離心率のスパイク
- 火星の掃除人
- デジタル太陽系儀
- オスカル国王への答
- 月に助けられた
13 自然界の不均衡
- サメと小エビ
- 超高速増殖ウサギ
- 成長の限界
- 状況の組み合わせ
- アオバエの産卵について
- ビートル力学
- 生命の網の目
- 流行病学におけるカオス
- HIV力学とエイズ
- 心臓停止!
- キックト・ローテイター
- 女王の屈伏
- ニワトリの心臓
- 医療数学
14 バタフライを超えて
- ランダムであるとはどういうことか
- 偶然とカオス
- 脈動する星々
- 短期予測
- 現実の世界
- Fracmat計画
15 フォン・ノイマンの夢
- ピンボールの魔術師
- 再びサドルへ戻れ
- 不規則に彗星へ
- 賢いペースメーカー
- バブロヤンツの脳波
- 脳はカオスを必要とする
16 カオスと量子
- 波動、粒子、そして量子
- 波動関数
- 箱の中の猫
- EPRパラドックス
- ボームの解釈
- ベルの不等式
- サイコロと決定論
- 穴だらけのたらい
- 「もし」の世界
17 深遠なる思考よ、さらば
- 偉大なる知性とかなりの知性
- デザイナー・カオス
- くり返しのきかない実験
- カオスへの夢遊
- リアルな数学を求める運動
- 今後さらなる変化が...
- 複雑性の保存
- 機械の中の山羊
- 単純性理論
- 代替可能性
- アリの国
- 単一性と連結性
結語:神とサイコロ遊びを...
訳者あとがき
参考文献
人名索引
事項索引
内容紹介:
神はサイコロ遊びをするか?現代科学が抱える難問の核心にあるカオスの正体に迫る。
近年広い分野で興味を持たれているカオスに関連した自然現象を、ほとんど数式を用いずにわかりやすく説明し、豊富な例え話とともに複雑な理論へ導いていく。1992年刊(382ページ)のものに新たに4章を加えた増補新版。
1998年10月刊行、519ページ。
著者について:
イアン・スチュアート(Ian Stewart)
ウォーリック大学数学部教授。英国の第一線の数学者であり、ポピュラーサイエンス書の著者としても世界的に有名。2001年に、王立協会のフェローとなる。新聞や雑誌の記事の執筆、テレビの科学番組への出演なども積極的に行っている。著書に、『数学の秘密の本棚』『世界を変えた17の方程式』『数学で生命の謎を解く』(いずれもSBクリエイティブ)、『もっとも美しい対称性』(日経BP社)、『自然界の秘められたデザイン』(河出書房新社)などがある。
イアン・スチュアートの著書日本語版: 単行本検索 Kindle版検索
イアン・スチュアートの著書英語版: ペーパーバック検索 Kindle版検索
理数系書籍のレビュー記事は本書で436冊目。
とにかく読み応えがあり、知的興奮を与えてくれた科学教養書である。フランスの数学者アンリ・ポアンカレが20世紀初頭に(後にカオスと呼ばれるようになる)不規則な天体の軌道の有り様に気づいて以来、このカオス理論と呼ばれる数学は、さまざまな道具とアイデアを駆使して発展してきた。特に1960年代以降、コンピュータが利用され始め、1970年代以降にコンピュータ・グラフィックスが利用できるようになり、カオスは目に見える形で姿をあらわし、研究に拍車がかかった。
カオスとは一般用語では「混沌」という意味だ。自然現象や人間が営む社会活動、経済活動、そして変化するあらゆるものには、不規則で取り扱いが難しいものが多い。そのうちのいくつかは、確率的、統計的に扱うことで平均的なふるまいを把握することができる。完全にランダムでその挙動が予測できない現象も、たとえば気象予報のようにコンピュータで取り扱うことができるものがある。カオス理論の起源は天体力学だが、適用できる対象は「およそ不規則に変化するあらゆる領域」にまで広がっている。
しかし、カオス理論が扱う対象は、確率や統計学的に見られる「平均値化」とは相入れない不規則な動きをもっている。将来の動きが予測できないのだ。とはいってもまったくランダムということではなく、不規則性の中に一定の秩序や数値であらわされる法則や性質をその中に見つけることができる。そのために、人間の目からはまったく異なるカオス現象であっても、共通した手法でアプローチすることができるようになるのだ。
また、混沌の中に秩序があることがわかると、その不規則な挙動に影響を加えることで、そのカオス的挙動を利用して人間の生活に役立てることができる場合がある。「カオス制御」と呼ばれる新しい工学分野は、すでに医療分野で利用し始めただけでなく、宇宙船に対してカオス的軌道を利用することで、より燃料効率のよい形で目的地の天体まで到達させることができるようになると予想されている。
本書はまた、カオス理論の発展史を知る上でも、最良の本だと思われる。言葉を尽くして具体的に詳細を語ることで、読者にとって読みやすい本となっている。質の良さはさることながら、ページ数が多いのはそのためだ。
章立てはこのとおりである。
プロローグ:時計仕掛けかそれともカオスか?
1 秩序から混沌へ
2 万能方程式を求めて
3 誤差の法則
4 最後の普遍学者
5 単方向振子
6 ストレンジ・アトラクター
7 お天気工場
8 カオスの調理法
9 センシティブ・カオス
10 フィッグ・ツリーとファイゲンヴァリュー
11 ほんものそっくりの感触
12 再びヒペリオンについて
13 自然界の不均衡
14 バタフライを超えて
15 フォン・ノイマンの夢
16 カオスと量子
17 深遠なる思考よ、さらば
結語:神とサイコロ遊びを...
プロローグ:時計仕掛けかそれともカオスか?
この世界はニュートンが予言するように時計仕掛けなのか、それともアインシュタインが言及したように「神はサイコロを振らない」のか、それとも「振る」のか?現代物理学は「振る」ほうに軍配を上げていて、それでは「神はどのようにサイコロを振るのか?」という問いに答えるまでになっている。そこに至る過程で測定、予測可能性、理論の実証、それに対する反証など新たな疑問が生じてくる。そのかわりに、複雑に見えるものが単純なものになってしまうこともあるし、逆に、一定の構造をもたず、でたらめに見える現象も実際には単純な法則に従っているかもしれない。決定論カオスは、それ自身の法則をもち、新たな実験技術に対して指示を与える。自然界の現象は非常に多様であり、それらのあるものは、カオスの数学の物理的対応物でありうる。液体の乱流、地磁気の逆転、心臓の鼓動の不規則性、液体ヘリウムの対流パターン、天体の回転、小惑星帯の空隙、昆虫の個体数の増加、水道の蛇口から出るしずく、化学反応の進行、細胞の新陳代謝、天候の移り変わり、神経パルスの伝播、電子回路の振動現象、ブイに係留してある船の振動、ビリヤードボールの跳ね返り、気体原子の衝突、量子力学の根底にある不確定性。--- これらは、カオスの数学がこれまで扱ってきた問題のいくつかの例である。
1 秩序から混沌へ
ニュートンからラプラスまでの力学の歴史を解説し、この世界は時計仕掛けのように未来が決まっているのか?それとも確率的にしか予測できないのかについて考察を進める。また、そのどちらでもない不規則な現象が存在していることを、いくつかの例を取りあげて紹介する。ヒペリオンという惑星が見せる不規則な挙動、電卓で反復計算する際にあらわれるカオスなどである。
2 万能方程式を求めて
古代の天文学、アンティキティラと呼ばれる古代ギリシャの惑星軌道計算機、コペルニクスからニュートンの宇宙観に基づく宇宙観の歴史、オイラーからフーリエ、ラグランジュ、ハミルトンに至る解析学史、決定論的には解くことのできない現代のさまざまな問題が紹介される。
3 誤差の法則
確率論、統計学の歴史を解説し、その中で確率分布、誤差や平均はどのように現実の対象を結びついているかを論じる。多数の集団を扱う統計力学が解説される。また、その中に見られるランダム性は、実はランダムではなかったということに気づき、それは「必要な情報が不足している」ことによる見かけのランダム性であったと解釈された。また、19世紀末までに科学は数学モデルの構築に対して2つのパラダイムを獲得していた。昔からあった決定論的な微分方程式を利用する解析学、そしてもうひとつは高度に複雑なシステムにおける運動を、平均という大ざっぱな特徴を表現する統計解析であった。そして、ほとんどの科学者は単純な決定論的系がランダムな系に似た振る舞いをするということに否定的だった。
4 最後の普遍学者
アンリ・ポアンカレの登場である。彼の片方の足は19世紀に、そしてもう片方の足は20世紀に置いた格好で両足を広げ、数学史の転換点にそびえるがごとく立っていた。彼の功績のひとつは、力学系における定性的理論の基礎を築いたことである。ポアンカレには学問的な懐の深さはあったが、天体の複雑極まりない軌道を照らし出す道具は持ち合わせていなかった。このカオスの深淵に光を当てて、その美しさを照らし出すためには、コンピュータや、その関連技術の助けが必要だった。したがってポアンカレは微分方程式にもとづく定性的な理論で武装したのである。その過程で彼が利用したのがトポロジーだった。ホモクリニック軌道、ヘテロクリニック軌道は、トポロジーに対して新たに導入した「ポアンカレ断面」というアイデアによって発見された。(参照:「ポアンカレ 常微分方程式 -天体力学の新しい方法-」、「ポアンカレによるカオスの発見と先見性」)
5 単方向振子
解析的な手法では解くことができない、非線形振子の問題が取り上げられる。この問題はトポロジーの幾何学の表現に映され、「エネルギー」という視点から解く方法が発見された。そしてこの抽象空間を利用した解法は多次元化され、幾何学の多次元かが進んでいくのである。
6 ストレンジ・アトラクター
微分方程式の解の安定性についての解説が始まる。 シンク[吸い込み口]、ソース[湧き出し口]、サドル[鞍部]、リミットサイクル[極限周期軌道]など、相空間に描かれる対象、基本的な用語を図を使って説明する。そして準周期的運動の表現に必要になる形がトーラスである。この章ではまた、スメールの研究が解説される他、カオス理論に新しく追加された構造安定性、アトラクター、巻き込み写像、カントール写像などが紹介、解説される。
7 お天気工場
天気の数値予報がこの章のテーマである。大気という連続体を離散的に取り扱って計算するのが数値予報である。カオス理論はその初期値鋭敏性という性質により、観測精度をどんなに上げても、コンピュータの性能をどんなに上げても完全に天気を予測することはできない。また、初期値鋭敏性は「バタフライ効果」として知られる現象をもたらす。バタフライ効果が実際におこっていることは、計算によりすでに確認されているのだ。気象の数値予報の研究を進める中で1963年に発見されたのが、「ローレンツ・アトラクター」である。
8 カオスの調理法
カオスの研究手法として考案された「スメールの馬蹄写像」、「ロジスティック写像」が解説される。そしてロジスティック写像の中に「周期倍増型カスケード」と名付けられたカオスがあらわれていることを確認する。つまり、カオスの中に秩序が存在することが発見されたのである。この章はカオス理論の1940年代から1970年代の研究を解説した章だ。
9 センシティブ・カオス
水の流れをテーマに、カオスの奥深さが語られる。水道の蛇口から落ちる水滴は、蛇口をひねるにつれて一定間隔リズムで、次に不規則なリズムになり、層流から乱流へと変化する。この過程で2回の状態遷移がおきているのだ。また、回転する車輪で生じる振動(ウォッブル)、流体力学で見られる乱流がカオスであることが紹介される。その解明のために考案されたアイデア、数学的手法が紹介される。この章で重要な概念として解説されるのがカオス振動の「パワー・スペクトル」である。また、時系列に沿った振動の観測量は1次元である。この系列をシフトして3つの系列にして、3次元の図形としてアトラクターを構成する「パッカード-ターケンス法」という手法が紹介される。この手法によって1986年、したたり落ちる水道水の水滴からアトラクターの再構築に成功した。つまり不規則に見える水滴のしたたりには秩序があったのである。また「レスラー・アトラクター」が紹介されるのもこの章だ。
10 フィッグ・ツリーとファイゲンヴァリュー
1970年代半ばのファイゲンバウムによるウィルソンのくりこみ法を乱流に応用する研究がこの章で紹介される。キーワードはフィッグ・ツリーとファイゲンバリューだ。手始めにロジスティック写像から始めた。当時利用できたHP-65というプログラム電卓を利用して数値の反復計算を行なったのである。その後継機であるHP-67はスマホアプリとして入手できるし、プログラムは単純なので、どうせならこの機種を使ってご自身で試されるとよいだろう。(もちろん他のプログラム電卓でも構わない。ちなみにCASIO高精度計算サイトのこのページでも計算することができる。) そしてこの章で重要なことは、ファイゲンバリューなどカオスを判定するための定量的な値が存在することが発見されたということである。
11 ほんものそっくりの感触
海岸線のギザギザな形は、その部分を拡大すると、似たようなギザギザがあらわれる。自己相似形であるといってよい。この章で紹介されるのは「フラクタル」である。そして整数値をとらないフラクタル次元が解説される。またフラクタルもカオス理論にとって欠かすことができない。フラクタル次元数を測定することで、カオスの判定に使えること、乱流に対するフラクタルとカオスとう2つのアプローチは「姉妹」であることが発見される。つまり、ストレンジ・アトラクターはフラクタルだったのである。この章では「マンデルブロ集合」、「ジュリア集合」が紹介される。ただし、乱流がフラクタルであるとするのは早急だ。また、フラクタルを利用した画像圧縮技術も紹介される。
12 再びヒペリオンについて
カオス的な回転をする土星の衛星「ヒペリオン」のメカニズムが詳しく解説される。また、衛星や惑星、小惑星の公転がもたらす共鳴現象を解説する。共鳴は(エネルギー保存系の力学である)ハミルトン系の力学において特に重要で、カオスはしばしばそれらの共鳴現象として生じることが多い。共鳴現象は、また小惑星帯の空隙(ギャップ)の謎も解明した。そもそも太陽系全体は本質的にはカオス的であることが示される。
13 自然界の不均衡
生態系における動物の個体数がカオス的に変化することを紹介する。生態学(エコロジー)に関する一般的な書物や、あるいは環境保護団体からきた寄付集めの手紙を見ると、それほど読み進まないうちに「自然界の均衡」という言葉に出会う。つまり、すべての種は、人間たちによっていとも簡単に壊されてしまうような、非常にデリケートな「生命の編目」で結びつけられているとかのおとぎ話が書いてあるのだ。この種の議論にはおかしなところがたくさんある。定常状態といえども、そのまま衰弱するのではなく移動してカオスにより、安定性の破壊が生じることもある。アトラクターの概念は、このような問題にも自然かつ有用なイメージを与えてくれる。多くの人々は単純明快な答を求めるし、またほとんどの政治家たちや圧力団体は単純明快なスローガンを求める。生態系はこのような人々にとってはあまりに複雑すぎるのだ。カオス理論は、このような複雑性がもたらす問題を解決してくれるのではなく、むしろ、そのような問題があることをわれわれに認識させてくれるのである。またこの章ではカオス理論の研究がHIVウィルスや心不全など脈動する臓器の研究にも有用であることを紹介している。
14 バタフライを超えて
ランダムであることとカオスはどのように違うのかを、とても詳しく解説する。そしてそれらの違いが、現実世界における予測とどのように結びついているか、どのように応用されているかが紹介される。そして、最後にバネの製造の例をとりあげ、その歩留まりを抑え、不良な製品をどのようにして減らすことができたかという、カオス理論の工業的な応用例が紹介される。
15 フォン・ノイマンの夢
1950年頃、偉大な数学者ジョン・フォン・ノイマンは微小擾乱(バタフライ効果)に対する天候の敏感性についてはじめて耳にしたとき「天候は予測不可能ではない。それは制御できる。」と述べたそうだ。将来、優れた計算機を持つようになったら、たちまち気象現象を2つの範疇にはっきりと仕訳できるようになるだろう。安定なものと不安定なものに。そして安定なすべてのプロセスをわれわれは予測できるであろう。また不安定なすべてのプロセスをわれわれは制御できるだろう。」つまり、天候にちょっと干渉するだけで大きな効果を及ぼせるのはもうわかっているのだから、どんなに大きな効果でも望みどおりに引き起こす経済的な方法が存在するはずである。カオス制御の話だ。
ここまで読んだとき、僕は昨年の台風15号、19号による豪雨被害のことを思わずにはいられなかった。事前に予測できていれば、わずかの影響を大気に与えるだけで、数日後の台風の進路や豪雨域を海上にそらすことができたかもしれない。現在は無理だが、将来そのような技術が実現することを切に願っている。
また先日、この連続投稿がツイッターでバズった。(連続投稿を開く)
三体問題のカオス的軌道を採用することで、それまで最も効率的と考えられてきたホーマン軌道を採用する場合の半分の燃料で宇宙船を月の周回軌道に乗せることができる。ただし地球を48周、月を10周回るため2年かかるが、将来月面基地建設のための物資を運搬するためには効率的だ。

フォロワーや読者の中には「カオスの初期値鋭敏性があるから、このようなことは不可能だ」と主張する方がいたが、実はそうでもない。月に到着する直前で軌道がぐにゃりと曲がっている場所がある。これは慣性に任せたカオス的軌道ではなく逆噴射して軌道修正したことによる。つまり、その場所まではカオス的軌道に任せ、最後の最後で燃料を使っているのである。また、途中で燃料をわずかに使って軌道を微修正することも可能である。このようにすればホーマン軌道の半分の燃料で済むのだ。
また、この章では脳波の研究にカオス理論のアトラクターが使われていることも紹介される。
16 カオスと量子
量子力学の不確定性原理も予測を不可能にする原因である。カオスのそれとどのように関連付けて考えればよいのだろうか?この章では、量子力学の発展史を解説した後に、まだ解明されていないこの領域の考察を深めている。
17 深遠なる思考よ、さらば
最終章は、複雑系と呼ばれる分野の解説だ。カオス理論が「単純な規則から不規則性が生まれる」ことであるのに対して複雑系は逆である。本書が刊行された頃に注目されてきたのが複雑系である。これについては、簡単に述べるにとどめ、本書の後に続編として刊行した「The Collapse of Chaos(カオスの崩壊)」で詳しく解説をするとしている。
また、この章では理論物理学者の多くが信じている「要素還元主義」について紹介している。素粒子の挙動がすべての自然現象の根源にあるとするこおの思想は、古代ギリシャからあった考え方だ。しかし、現実の問題はスケールに応じて別々の理論で理解され、それらの間に存在するギャップは大きく、それを埋めることはほぼ不可能な状況である。そのことを象徴的に示しているのが「ラングトンの蟻」という不思議なカオス現象である。この現象については、ここから始まる連投ツイートで紹介しておいた。色の数を増やしたもの、3Dバージョンにしたものなど、不思議で美しい動画が見れるので、ぜひご覧いただきたい。
ラングトンの蟻(解説動画)

ラングトンの蟻(2D多色版+解説動画、3D多色版動画)

ラングトンの蟻の不思議は数学的に解決されていない。不規則なカオス的挙動から、なぜ突然「道」が作られ始められるのか?蟻の運動を決める規則はごく単純なものなのだ。この謎は解明されていないし、数学的に証明もされていない。何が解明されていないかは、このスライドに書かれている。
ツイッターでアンケートをとってみたところ、114人の方から回答をいただき、92.1パーセントの方が「ラングトンの蟻」をご存知ないという結果になった。(アンケートを見てみる)

ラングトンの蟻でできる「道」や「規則的な幾何学図形」は、このカオス現象におけるアトラクターである。これを観たとき僕は、将棋で互いに最善手で指すうちに偶発的に生じる「千日手」のようなものではないかと思った。千日手では同じパターンの指し方が無限に繰り返されるからだ。
ざっと本書の内容を章別に紹介させていただいた。絶版なので安い中古本を見つけることができたら、ぜひお読みいただきたい。
日本語版は新版と旧版が販売されている。できれば新しいほうを買ってほしい。
「カオス的世界像―非定形の理論から複雑系の科学へ: イアン・スチュアート」(1998年、増補新版、519ページ)
「カオス的世界像―神はサイコロ遊びをするか?: イアン・スチュアート」(1992年、初版、382ページ)


増補新版の検索: Amazon 日本の古本屋 ヤフオク メルカリ
増補新版の翻訳のもとになった原書はこちら。Kindle版は安く買える。
「Does God Play Dice?: The Mathematics of Chaos: Ian Stewart」(Kindle版)

本書の続編は「The Collapse of Chaos(カオスの崩壊)」というタイトルで1994年に刊行された。
「The Collapse of Chaos: Discovering Simplicity in a Complex World: Ian Stewart」(Kindle版)

そして同じ著者が「神はサイコロ遊びをするか?」ではなく「サイコロは神遊びをするか?」という本を書いていることに気がついた。Kindle版はすでに発売され、ペーパーバック版は6月、ハードカバー版は9月に発売される。
「Do Dice Play God?: The Mathematics of Uncertainty: Ian Stewart」(Kindle版)

関連記事:
ポアンカレ 常微分方程式 -天体力学の新しい方法-
https://blog.goo.ne.jp/ktonegaw/e/8dc81ef7e48c812b56befcc2345d59d4
天体力学のパイオニアたち 上: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/5c51d50e2141c8ae58c9323ad49b65a1
天体力学のパイオニアたち 下: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/88846fbb12ed1f8b11a49f0659b93c75
数理解析のパイオニアたち: V.I.アーノルド
https://blog.goo.ne.jp/ktonegaw/e/165c894d023b1174fd519522935cdeeb
Hirsch・Smale・Devaney 力学系入門 ―微分方程式からカオスまで― 第3版
https://blog.goo.ne.jp/ktonegaw/e/98d451af90b7efc63aacbe4efdb330fa
力学系カオス: 松葉育雄
https://blog.goo.ne.jp/ktonegaw/e/12392ac282d10deed28914d8182c2286
「磁石振り子」によって現れるカオス軌道とフラクタル図形
https://blog.goo.ne.jp/ktonegaw/e/d47ee62678af4791420f81c70ef8002f
メルマガを書いています。(目次一覧)

応援クリックをお願いします。




「カオス的世界像―非定形の理論から複雑系の科学へ: イアン・スチュアート」

増補新版への序文
プロローグ:時計仕掛けかそれともカオスか?
1 秩序から混沌へ
- 不条理な論証
- 時計仕掛けの世界
- ヒペリオンへの旅
- カオス
- 電卓カオス
- ヒンズー教におけるメンテナンスの技法
2 万能方程式を求めて
- 天球の回転
- ギリシャで生まれた歯車
- 太陽中心説
- 振子の運動
- 重力(万有引力)と幾何学
- 世界の体系
- 鐘と笛
- 風と波
- 解析学が見捨ててきたもの
- 質入れされた数学
- 再定式化の時代
- 市場は大騒ぎ
3 誤差の法則
- ギャンブルで勝ちたい!
- 並の人、または「平均人」という概念
- 遺伝研究の天才=形質遺伝と正規分布
- テクノロジー・トランスファー
- オランダ生まれのカオス
- パラダイムを延命する
4 最後の普遍学者
- うっかり屋の空想家
- 数学のオスカー
- ラバーシート・ダイナミックス
- 四方八方めったらやたらに大突進
- 三角関係のもつれ
- トポロジーへの一つの疑問
- 天上のカオス
5 単方向振子
- 勝てないときはずるをする
- エネルギー曲面上の幾何学
- 非ゾウ学
- 円に線を巻きつけて
- 事実は摩擦より奇なり
- 多次元の夢
- n次元空間における幾何学
6 ストレンジ・アトラクター
- 光陰矢の如し
- シンク[吸い込み口]
- ソース[湧き出し口]
- サドル[鞍部]
- リミットサイクル[極限周期軌道]
- 典型的にはまさにこれ
- 猫を振りまわして
- 日に映る景色ではなく精神に映る景色
- 構造的安定性
- アトラクター
- 巻き込み写像
- カオスの足跡
- ポアンカレ断面
- 宙ぶらりんのソレノイド
- カントールのチーズ
- ほんもののカオス
- 痛烈なこきおろし
7 お天気工場
- 輝かしき失敗
- お天気チェス
- 0と無限大の間で
- メガフロップ
- 心の中は数学者
- 滞留せずに対流に挑む
- コンピュータのおかげです
- バタフライ効果
- その蝶をたたき落とせ
- 引き延ばしと折りたたみ
8 カオスの調理法
- 引き延ばしと折りたたみ
- レーダーから馬蹄まで
- ディナミックス・ボロニェーズ
- 磁気トラップ
- パフ・ペイストリー
- ミセス・ビートンを越えて
- ロジスティック写像
- 定常状態レジーム
- 周期倍増型カスケード
- カオスの中にある秩序
- 大きなノミ、小さなノミ
9 センシティブ・カオス
- 奥の深さを見抜くには
- ウォッブルが雪だるま式に
- ありそうもない筋書き
- 反証可能性
- 古典的室内実験
- レーザー光の照射
- 出会いと接点
- でっちあげの観測可能量
- ストレンジ・ケミストリー=化学反応の不思議
- 芭蕉再訪
10 フィッグ・ツリーとファイゲンヴァリュー
- 宇宙の大海原に漂う一本の壜
- 摂動はダメ、くりこみだ!
- 大型汎用コンピュータを使わない利点
- 蛇と熊
- くりこみ法
- ファイゲンバウムの写像
- ファイゲンバリュー
- 両刃の剣
- 空想の世界で乱流を見る
- 極寒と静寂の世界
- ヘリウムの回転運動
11 ほんものそっくりの感触
- 測定の尺度
- 雪片と海岸線の形
- 1 1/4 次元
- 「幾何学だけはやらないほうが...」
- シリコン・バレー
- 凝集と浸透
- 水と油はどうして混ざり合わないか?
- 万物と宇宙
- フラクタル偽造物
- 雲と雨
- 実は姉妹だった!
- ジンジャーブレッド・マン
- フラクタルの牛
12 再びヒペリオンについて
- 宇宙のじゃがいも
- バンパイヤ・ドッペルゲンガー
- スピン軌道の幾何学
- 潮汐摩擦
- どうして、そういうことになったのか?
- 共鳴現象
- カーターウッドのすきまとヒルダのかたまり
- 高離心率のスパイク
- 火星の掃除人
- デジタル太陽系儀
- オスカル国王への答
- 月に助けられた
13 自然界の不均衡
- サメと小エビ
- 超高速増殖ウサギ
- 成長の限界
- 状況の組み合わせ
- アオバエの産卵について
- ビートル力学
- 生命の網の目
- 流行病学におけるカオス
- HIV力学とエイズ
- 心臓停止!
- キックト・ローテイター
- 女王の屈伏
- ニワトリの心臓
- 医療数学
14 バタフライを超えて
- ランダムであるとはどういうことか
- 偶然とカオス
- 脈動する星々
- 短期予測
- 現実の世界
- Fracmat計画
15 フォン・ノイマンの夢
- ピンボールの魔術師
- 再びサドルへ戻れ
- 不規則に彗星へ
- 賢いペースメーカー
- バブロヤンツの脳波
- 脳はカオスを必要とする
16 カオスと量子
- 波動、粒子、そして量子
- 波動関数
- 箱の中の猫
- EPRパラドックス
- ボームの解釈
- ベルの不等式
- サイコロと決定論
- 穴だらけのたらい
- 「もし」の世界
17 深遠なる思考よ、さらば
- 偉大なる知性とかなりの知性
- デザイナー・カオス
- くり返しのきかない実験
- カオスへの夢遊
- リアルな数学を求める運動
- 今後さらなる変化が...
- 複雑性の保存
- 機械の中の山羊
- 単純性理論
- 代替可能性
- アリの国
- 単一性と連結性
結語:神とサイコロ遊びを...
訳者あとがき
参考文献
人名索引
事項索引























1つのスリットを通り抜けた光をスクリーン上で見るとき、そのどこに光のつぶつぶが来るのかは予言できません。
ところが、その場所を指定するとそこに光(または電子)がやってくる確率はわかるということなので、私などもひょっとしてカオス的なメカニズムがあるのではなどと考えたりしたこともあります。もちろん論文にできるほど突っ込んで考えたことはないのですが。
しかし、そういう考えで光の干渉縞が説明できたという話も聞きませんし。そういう考えはたぶんオカルト的でもあると思っています。
そこら辺をもっと突っ込んだ説明があるのかなと思い、カオスと量子的振舞いとの関係がつかないかとむかし空想した自分を思い出して、興奮しています。
「カオスと量子」の章の分量はそこそこ多いので、とても説明しきれませんが、この章では一通りの量子力学史、つまり前期量子論からベルの不等式、量子エンタングルメントまで解説します。
量子力学が正しいことは「ベルの不等式」が破れたという実験的事実により最終確認されました。
最終決着「ベルの不等式」の破れの実験
http://www.nikkei-science.com/201902_054.html
すなわち、量子力学ではない古典物理学では、ベルの不等式は破れていないわけです。カオス理論は古典物理の数学理論ですから、ベルの不等式は破れていないはずです。
この章で紹介されているのはパルマー博士のアイデアです。博士のアイデアによるとカオスを前提としたときでも、ベルの不等式をすり抜ける(つまり破れる)ことがあり得るということだそうです。
日本語で書かれた適切なページが見つからないので、最近arXiv.orgに投稿されたパルマー博士の論文を2つ紹介します。
T.N.Palmer
Experimental Non-Violation of the Bell Inequality
https://arxiv.org/abs/1709.01069
Bell Inequality Violation with Free Choice and Local Causality on the Invariant Set
https://arxiv.org/abs/1903.10537
本書の「カオスと量子」の内容に沿ったものではありませんが、このようなページを見つけました。
Quantum chaos
https://en.wikipedia.org/wiki/Quantum_chaos
An Introduction to Quantum Chaos
https://arxiv.org/abs/nlin/0107039
あと、アマゾンで検索すると次のような本が見つかりました。
「量子物理学におけるカオス」
中村 勝弘
「カオスの素顔―量子カオス、生命カオス、太陽系カオス… (ブルーバックス)」
ニーナ ホール
この理解はまちがっていますか。
中村勝弘さんの本があることは知っていましたが、その本をまだ見たことこともありません。
ともかく、カオスと量子力学とを関連づけて考えている人は私だけではないようです。
もっとも私はこれはオカルト的かなと思ってはいるのですが。
話はべつですが、1次元のマッピングを疑似乱数の発生法として使えないかと考えたことがありました。
これはそのような論文がインド人か誰かによって書かれているようです。うまくいったかどうかは私にはわかっていません。
量子力学とカオス理論は直接のつながりを持っていないと思います。ただし量子に関しても3体以上の問題がありますから、その意味ではカオス現象は発生します。
量子力学とカオス理論は、次のような点で研究しなければならないと個人的に思っています。
- 不確定性原理が示すミクロの限界と馬蹄による無限小に接近した軌道がどのように整合性をもつのか
- 量子力学の三体以上の問題をどのように扱うか
- ベルの不等式をカオスはどのようにすり抜けるのか
不勉強ですので、これ以上のことはわかりません。
カオスかと思ったら規則パターンに落ち込むとは、カオスもなかなか多難ですなー。
規則パターンになることは実例を示せば証明になると思いますが、カオスのままで永久に続くことは証明困難でしょう。
ひょっとしたらカオスと思ってる全部がいづれ規則パターンに落ちてしまうけど、人類の計算能力では分からないだけってこともあるかも知れません。
いづれ規則パターンであっても予測できなきゃカオスなんでしょうが。
似た話と言って良いかわかりませんが、昔聞いたBaire関数でも人類の限界を痛感したもんです。
0階級のBaire関数は連続関数で、その極限として定義されるのが1階級のBaire関数、さらにその極限で2階級,3階級,…と無限に存在するんですが、人間が実例を作れるのは2階級まで、その先は存在するけど手が届かないとか。
この手の人類が絶対届かないものがある話もSFネタになって面白いですね。
コメントありがとうございます。
ラングトンの蟻を見ていると「人類の限界」はあるのだと思えてきます。
ウィキペディアで「ベール関数」の項目を読んでみました。基礎的なレベルでも関数にはとらえどころのない不思議な世界があるのですね。