
先日、この連続投稿がツイッターでバズった。(連続投稿を開く)
三体問題のカオス的軌道を採用することで、それまで最も効率的と考えられてきたホーマン軌道を採用する場合の半分の燃料で宇宙船を月の周回軌道に乗せることができる。ただし地球を48周、月を10周回るため2年かかるが、将来月面基地建設のための物資を運搬するためには効率的だ。
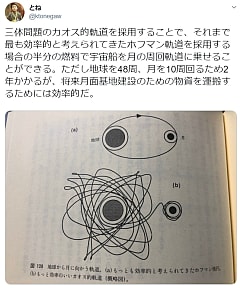
20世紀初頭、カオス現象と呼ばれるこの不規則な動きが存在することに初めて気がついたのは、フランスの数学者ポアンカレである。
ジュール=アンリ・ポアンカレ(Jules-Henri Poincaré、1854年4月29日 – 1912年7月17日):ウィキペディア
ナンシー生まれのフランスの数学者、理論物理学者、科学哲学者。数学、数理物理学、天体力学などの重要な基本原理を確立し、功績を残した。フランス第三共和制大統領・レーモン・ポアンカレはアンリの従弟(いとこ)。
彼は惑星の軌道の安定性を数学的に研究する手始めに「制限三体問題」と呼ばれる天体力学、軌道計算の問題に取り組んでいた。「制限」とは「運動が平面内に限られる」という制限のことである。一般の三体問題よりは解きやすい。
しかし、それを解くための微分方程式の研究を進めるうちに、軌道が無限に分岐するという奇妙な現象に彼は気がつき、この想定外の結果に彼はとても驚くことにある。その経緯は「ポアンカレ 常微分方程式 -天体力学の新しい方法-」という記事で紹介した。ポアンカレは見つけた2つのタイプの無限分岐軌道にそれぞれ「ホモクリニック軌道」、「ヘテロクリニック軌道」という名前を与えた。
ポアンカレが研究していた時期は、1927年に発表された量子力学の「不確定性原理」が発表される20年以上前のことである。力学の微分方程式は、少なくとも数学的には未来を完全に予測するという考えが受け入れられていた。また、確率的な現象は確率論として定着していたが、物事の初期状態さえ知っていれば、未来は完全に予測できると考えられていた。未来を予測できないのは、初期状態に関する情報が不足しているからだと理解されていたのである。
ポアンカレが発見した軌道の無限分岐は、その常識を破ってしまった。初期状態がほとんど同じであっても、その後の経過は時間が経つにつれて、とても異なる状況になってしまうのだ。彼が見つけたことを図であらわすと、次のようなものになる。


ホモクリニック軌道の分岐は、次の動画で確認することができる。コンピュータのない時代に、ポアンカレはこのような軌道の姿を想像していたのだ。
C14ホモクリニック分岐
MoeckelRick「三体問題の混沌」
ニュートンの「三体問題」を読む(ファビオ・パクチ)
初期状態が少しでも違うと結果が大幅に違ってくるということは「初期値鋭敏性」と呼ばれる、カオス現象がもつ性質の代表例だ。その後、カオス現象を研究する「カオス理論」という数学領域は1960年代以降に大発展し、カオス現象に共通する性質がいくつも見つかることになる。(1961年、エドワード・ローレンツにより、簡単な微分方程式から作られる天気予報の気象モデルの数値計算結果がカオス的な振る舞いをすることが発見された。1963年、この結果はテント写像により引き起こされるカオスとして発表された。)
天体の軌道に関する初期値鋭敏性は、次の動画で確認することができる。再生開始2分あたりから軌道が分岐する。
制限三体問題:
カオス現象では初期値鋭敏性のために予測が不可能になるわけだが、未来が決定していないということではない。正しく言えば「未来は決定しているが、予測ができない。」のである。
決定されているのに予測できない未来—世界観を覆した数学理論—
https://www.kyoto-su.ac.jp/project/st/st11_01.html
カオス現象の初期値鋭敏性は気象の世界では「バタフライ効果」として知られている。1匹の蝶の羽ばたきで大気が揺らぐ結果、数カ月、数年先の気象に影響を与えることがあるというたとえだ。コンピュータによる計算の結果、バタフライ効果が生じることが、すでに確認されている。(つまり、仮説ではない。)
天体の運動が無限分岐することの重大性を、ポアンカレは気がついていた。初期値鋭敏性や気象予報、物事の確率的振る舞いに関して、次のような文章を残している。
われわれが気づかないようなごく小さな原因によって、われわれが認めざるを得ないような重大な効果が引き起こされることがある。このようなとき、われわれはこの効果が偶然に起こったという言い方をする。もしも、われわれが自然の法則と宇宙の最初の瞬間の状態を正確に知ることができたとしたら、その後のあらゆる瞬時における同じこの宇宙の状態を、われわれは正確に予言できるはずである。しかし、たとえ自然の法則にそれ以上の秘密がなくなったとしても、われわれはその最初の状態を近似的にしか知りえない。もしもそのことが、その後の状態を同程度の近似で予見するのを許すことになるなら、このことこそがわれわれに必要なすべてであって、このときわれわれはその現象が予測され、そしてその現象は法則に支配されているというのである。
しかるに、つねに、このようになるとは限らないのであって、ときには初期条件のちょっとした違いが、最終的に起こる諸現象のなかで非常に大きな差異をもたらすようなことも起こるかもしれない。初期条件の小さな誤差が、最後に莫大な誤差を作り出すこともあるかもしれないのだ。このようにして、予測は不可能となり、われわれは偶然によって起こる現象を得るのである。
気象学者たちは、何ゆえに天気予報にこれほど苦労するのだろうか?われわれには、雨や嵐があたかも偶然に起きるように思えるのはなぜだろうか?多くの人々が雨乞いをしたり、晴天の祈りを捧げるのを不思議なことを思わないのはどうしてだろうか?しかも、その人たちは祈りによって日食や月食を起こそうとするのは、ばかげたことであると考えているにちがいないのだ。
一般に大気が不安定な平衡状態にあるような地域で大きな擾乱が生じていることがわかっている。気象学者たちは、このような平衡が不安定であり、どこかで低気圧が発生しそうであることはわかっているが、どこでそれが発生するかはわからないのだ。ある位置から緯度や経度にして10分の1度かそこらずれたあそこではなく、ここに低気圧が発生したために、その被害を免れたであろう地方に実際には被害が広がってしまうこともある。もしもこの10分の1度を知っていたら、われわれはこの災害を予見できたであろうが、しかし、観測はそこまで厳密でも正確でもない。そして、この理由のために、あたかもすべてが偶然によるものであるかのように見えるのである。
ルーレット遊びは、一見この例と何の関係もないように思えるが、実はそれほど変わりはない。100個のセクターに等分して、それらを赤と黒に交互に塗り分けた円盤の中心軸上で、針を回転させるものと考えてみよう。もしも針が赤のセクターで止まったら私の勝ち、そうでなければ、私の負けと決める。針は、いま仮に10から20回転するとしよう。しかし、私が回転の勢いを加減することによって、早めに止まったり遅く止まったりするだろう。
針が黒のセクターで止まるか、それともその次の赤のところで止まるかを決めるには、最初に回す力がたったの1000分の1、もしくは2000分の1違うだけで十分である。これはわれわれの筋肉の感覚ではわからないほどの、またもっとも精密な機器をもってしても識別できないほどの違いである。それゆえ、私には自分がスタートさせた針がどうなるか予見するのは、不可能である。だからこそ、胸をときめかせて、幸運がやってくるのを待つのである。
カオス現象では、未来の状態がまったくランダムに決まるということではない。一見不規則に見える現象の中に秩序やパターン、異なる現象の中に共通する性質があるのだ。それらを研究するのがカオス理論であり、その性質を利用したり逆手にとって人間の生活に役立てようとするのが「カオス制御」と呼ばれる研究領域だ。冒頭のカオス的な宇宙船の軌道もカオス制御のひとつである。
気象の数値予報は観測精度やスパコンの計算速度がどんなに向上しても、完全に予報することはできない。カオス現象は初期状態において無限の精度を必要とし、そのために必要なコンピュータのメモリーや演算速度は無限でなければなないからだ。現在、数値予報で正確に予報できるのはせいぜい数日先の天気までである。(しかし、ゲリラ豪雨はまだ予報できていない。)
ポアンカレが遺した文章の中の「その被害を免れたであろう地方に実際には被害が広がってしまうこともある。」という箇所に差し掛かると、昨年の台風15号、19号による豪雨被害を思い出さずにはいられない。あらかじめ進路がわかる場合、カオス理論のバタフライ効果を利用することで、事前にごく小さな影響を大気に与えて数日後の台風の進路を変えて豪雨域を海上にずらすことが将来できるようになればと切に願っている。
物理学や天文学や気象だけでなく化学、生物学、工学、医療、経済、金融や株式など、ありとあらゆる「不規則に変化する現象がある領域」でカオス現象は見られる。カオス理論やカオス制御から得られる効用は計り知れない。
関連記事:
ポアンカレ 常微分方程式 -天体力学の新しい方法-
https://blog.goo.ne.jp/ktonegaw/e/8dc81ef7e48c812b56befcc2345d59d4
天体力学のパイオニアたち 上: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/5c51d50e2141c8ae58c9323ad49b65a1
天体力学のパイオニアたち 下: F.ディアク、R.ホームズ
https://blog.goo.ne.jp/ktonegaw/e/88846fbb12ed1f8b11a49f0659b93c75
数理解析のパイオニアたち: V.I.アーノルド
https://blog.goo.ne.jp/ktonegaw/e/165c894d023b1174fd519522935cdeeb
Hirsch・Smale・Devaney 力学系入門 ―微分方程式からカオスまで― 第3版
https://blog.goo.ne.jp/ktonegaw/e/98d451af90b7efc63aacbe4efdb330fa
力学系カオス: 松葉育雄
https://blog.goo.ne.jp/ktonegaw/e/12392ac282d10deed28914d8182c2286
カオス的世界像―非定形の理論から複雑系の科学へ: イアン・スチュアート
https://blog.goo.ne.jp/ktonegaw/e/4ace135356ba99a1cb549bbbf073a591
「磁石振り子」によって現れるカオス軌道とフラクタル図形
https://blog.goo.ne.jp/ktonegaw/e/d47ee62678af4791420f81c70ef8002f
古典力学の形成―ニュートンからラグランジュへ:山本義隆
https://blog.goo.ne.jp/ktonegaw/e/e808487b7e9d668967f703396e32d80a
全5巻完結!:ラプラスの天体力学論(日本語版)
https://blog.goo.ne.jp/ktonegaw/e/a720b0cfb775d00625763f87a56b2414
発売情報: 惑星探査機の軌道計算入門: 半揚稔雄
https://blog.goo.ne.jp/ktonegaw/e/a3aba0b87bff8a8ae54fb37ad1b04504
メルマガを書いています。(目次一覧)

応援クリックをお願いします。


























