
この記事の元ネタ:「位相への30講:志賀浩二」のコラムより
4次元以上の多次元空間では日常感覚では理解できないことがいくつも明らかになっている。今日はそのひとつを紹介しよう。久しぶりの「理科復活プロジェクト」で、これは高校生や一般読者向けの記事である。(このカテゴリーの趣旨はこちらの記事で述べておいた。)
直径が1の青い円を4つ、下の図のように並べる。すると周りを囲む正方形の各辺の長さは2となる。このとき4つの円の真ん中の隙間に置いた赤い円の「半径」はどれくらいになるだろうか?

正方形の対角線の長さは 2√2 で青い円2つぶんの直径は2である。前者から後者を引いたものは赤い円の「直径」2つぶんになっていることに気がつくのにそう時間はかからないはずだ。よって赤い円の「半径」は次のとおり。
赤い円の半径=(2√2-2)/2/2=(√2-1)/2=0.207
同じことを3次元空間で考えてみたらどうなるだろう。図としてはこのようになる。
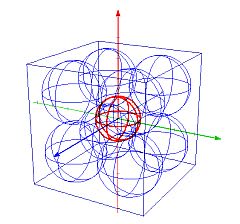
赤い球を囲む青い球の数は、2倍の8個となる。青い球の直径は1だから周囲の立方体の1辺の長さは2だ。そうすると立方体の頂点から反対側の頂点まで、これを「対角線」と呼ぶことにすれば、この長さはピタゴラスの定理を2回使えば2√3であることがわかる。すなわち赤い球の「半径」は次の式で計算できることがわかるのだ。
赤い球の半径=(√3-1)/2=0.366
2次元のときより赤い球は少し大きくなっている。
さらに4次元空間ではどうなるだろうか?図を思い浮かべることはできないが、4次元の世界では球は「超球」と呼んでいる。けれどもここでは単に「球」と呼ぶことにしよう。4次元の超立方体も「4次元立方体」と呼ぶことにする。
次元の数が1つ増えるごとに、周囲の青い球の個数は2倍になる。なぜなら次元の数1つ増えると青い球が2つ並ぶだけの長さの辺が1本増え、ひとつ低い次元のときに立方体に詰まっていた青い球の個数が既にあるひとつひとつの次元で2倍に増えるからだ。(わかるかな?2次元から3次元の場合を考えてみるとよい。)
4次元の青い球の直径は相変わらず1なので、4次元立方体の各辺の長さは2となり、対角線の長さはピタゴラスの定理を3回使って2√4=4となる。すなわち4次元の場合の赤い球の「半径」は次の計算で求めることができる。赤い球はさらに大きくなった。
4次元の赤い球の半径=(√4-1)/2=0.5
このように考えていくと、n次元空間の立方体の対角線の長さは2√nとなるから、赤い球の半径が次の式で計算できることだろう。
n次元の赤い球の半径=(√n-1)/2
おお、すごい!一般式は正しそうだ!
2次元のときでもちゃんとこの公式は使えるだろうか?2次元の球とは、つまり円のことだ。n=2を公式に代入して計算すると以下のようになる。ま、これは当たり前か。
2次元の赤い球の半径=(√2-1)/2=0.207
それでは、1次元のときも大丈夫だろうか?1次元の青い球とは、すなわち長さが1の青い線分であり、図にするとこんな感じで、球も立方体もつぶれてしまう。(立方体は長さ2の線分になる。図では真ん中の長い線が立方体で、上下にずらして描いた2本の線が2つの青球をあらわしているつもり。)

それでも公式を使えば赤い球(線分)の半径は次のようにゼロと求まる。赤い球の入る余地など全くないのだ。
1次元の赤い球の半径=(√1-1)/2=0
このように「公式」は一般的にn次元空間でも成り立ちそうなので、さしあたり15次元空間まで計算してみると、このようになった。(画像はクリックで拡大する。)

うーむ、素晴らしい。。。。それにしても青い球はずいぶんたくさんになるんだな。。。
あれ?何か変だぞ!!!
そう、10次元の行を見てほしい。真ん中の赤い球の「半径」は1.08になっている!つまり赤い球の「直径」は2.16となり、外側の10次元立方体からはみ出してしまうのだ。なぜなら立方体の辺の長さは何次元であろうと2なのだから。
10次元の青い球はすべて10次元立方体の中にあるはずなのに、その真ん中の隙間に収まっているはずの(10次元の)赤い球は10次元立方体の外にはみだしている!!10次元以上では赤い球の半径が1より大きいのでいつも立方体からはみ出しているのだ。
日常感覚では理解できないことが、高い次元の空間ではおきているのだ。今回のはその一例である。
関連リンク:
キス数:
http://blog.goo.ne.jp/ktonegaw/e/3fff2b46269846dff3db22e01744d085
n次元球の体積:
http://eman-physics.net/statistic/sphere_vol.html
応援クリックをお願いします!このブログのランキングはこれらのサイトで確認できます。


























数学的な3次元空間、私たちが3次元空間と思って住んでいる(物理的な)3次元空間のどちらにも「厚さ」はありません。あるのは縦、横、高さの方向だけです。
鈴木さまがおっしゃっていることは、リンゴの皮は2次元曲面ですが「厚さ」があると言っているのと同じです。しかし皮に厚さを考えた瞬間リンゴの皮は3次元(の物体)になります。
夏ミカンや「はっさく」のように皮の厚い果物もあるわけですからそのような意味での「厚さ」は予想したり計算したりできるものではありません。
申し訳ありませんがこの件と4次元宇宙論については、これ以上コメントをお控えいただきますようお願いいたします。(コメント入力いただいても公開しないことにさせていただきます。)
3次元空間だけに話を限ったとき、縦、横、高さの3つの方向以外に4番目の「厚さ」という方向は存在しません。
1つ次元を落とし、リンゴの皮と中身で考えるとわかりやすくなります。
1.私たちの3次元宇宙の厚さの問題
-> いえ、この点については大丈夫です。鈴木さまが「厚さ」と呼んでいるのは4次元方向に向いていますよね。ですので私たちが知覚できる3次元空間の中では宇宙は等方的に広がっています。リンゴの皮だけみると等方的に広がってますが、皮と中身を一緒に考えるとリンゴは等方的には広がっていません。
2.時間~時間はこのモデルにとってどのような意味があるのか。つまり時間の正体。私たちが使っている時間と4次元宇宙の時間とが同じものなのか?
-> 2つは同じ時間だと考えないと矛盾してしまいます。リンゴの皮と内部は同じ時間を共有しています。
3.4次元宇宙の内部の問題、これは私たちにとっては過去になりますが。
-> いいえ、時間は5次元目の次元ですから「内部」にはならないはずです。リンゴの皮と中身は「同じ時間」を共有してその時間はリンゴや皮の内部のことではありません。「過去」もリンゴの中にはありません。
僕自身はもし空間次元数が4以上である場合、4次元以上の空間次元はコンパクトに丸まっていなければならないと考えています。(カルーツァ-クライン理論や超弦理論もそうですね。)
その理由は次の記事に書いてありますが、もしわかりにくいようでしたら、前のほうの記事からお読みください。
多次元空間へのお誘い(16):物理的な問題
http://blog.goo.ne.jp/ktonegaw/e/fa024dbeb4e0454e12945d6ffcdc6502
多次元空間へのお誘い(17):問題を解決するためのアイデア
http://blog.goo.ne.jp/ktonegaw/e/5e9c9021e68cb05f37e029f4374add0f
1.私たちの3次元宇宙の厚さの問題
2.時間~時間はこのモデルにとってどのような意味があるのか。つまり時間の正体。私たちが使っている時間と4次元宇宙の時間とが同じものなのか?
3.4次元宇宙の内部の問題、これは私たちにとっては過去になりますが。
これらの難解な問題について考えていきたいと思っています。
鈴木さまが独自でお考えになった4次元宇宙モデルのことでしたか。
> 私の4次元宇宙モデルの概要はこういうものです。
> 時間に関係なく私たちの3次元宇宙は4次元宇宙の
> 一番外側になります。ちょうどリンゴの皮みたいなものです。
どのようなモデルかは理解できました。
鈴木さまはブログを書いていらっしゃるようですので、計算した数値だけでなく、計算手順、詳しい計算過程を数式を含めてお書きになるとよろしいかと思います。計算結果だけだと読者には理解できませんので。
また、その宇宙モデルが正しいかどうか?
計算結果が正しいかどうか?
については、どのように検証すればよいかもお書きになるとよいと思います。
私の4次元宇宙モデルの概要はこういうものです。時間に関係なく私たちの3次元宇宙は4次元宇宙の一番外側になります。ちょうどリンゴの皮みたいなものです。この4次元宇宙を使ってハッブル定数を計算したところ最新のハッブル定数の値に近いものになったので自信を得て現在の宇宙の大きさを計算しようと思いました。重要なことはこの膨張する4次元宇宙の膨張速度はちょうど光速にしないといけません。計算は易しいので貴方も計算してみてください。
私が最初初期宇宙の大きさを計算した式は過去未来にわたって宇宙の大きさを計算する式です。これを使えば初期宇宙の大きさはプランクの大きさ程度になるようです。この式で現在の宇宙の大きさを計算して4次元宇宙モデルで計算した宇宙の大きさとぴったり合えばよいのですが。
コメントありがとうございます。
初期宇宙のサイズはプランクスケール程度だと学んでいましたので、いただいたコメントには最初「?」だったのですが、「膨張する4次元宇宙モデル」というのは次の新説のことだったのですね。空間の次元数が4であったという説です。
宇宙の起源は4次元? 最大の謎に大胆な新説
日経サイエンス
http://www.nikkei.com/article/DGXMZO77444830U4A920C1000000/
初期宇宙の「初期」をどのタイミングで考えるかによってサイズはだいぶ違ってくると思います。一般相対性理論でも計算できるというのであれば、よほど大きくなった時点を想定されているわけですね。
4次元宇宙モデルはひとつの考え方ですが、通常の3次元宇宙もでる(インフレーション宇宙論)では、初期宇宙のサイズは以下のページの説明に書かれているように、プランクスケール程度のものすごく小さなものです。
誕生時の僕らの宇宙の大きさ
http://kajipon.sakura.ne.jp/kt/kt81.htm
宇宙創生を解明する「インフレーション理論」
http://www.athome-academy.jp/archive/space_earth/0000000243_all.html
初期宇宙に予想外の大きさを持つ構造、すばる望遠鏡が発見
http://www.astroarts.co.jp/news/2006/07/27subaru_large_structure/index-j.shtml
他の方法で宇宙の大きさを計算してみました。膨張する4次元宇宙モデルを利用する計算です。これはうまくいったようです。結果は8.16×10の23乗㎞になりました。これは一般相対性理論でも計算できるそうです。
電磁場に対して量子化という手続きを行うと、電磁場で生成・消滅する光子が説明できるようになります。
専門的には次のようなページで解説されています。
http://www.geocities.jp/eulers_formula/quantumelectronics2.html
http://homepage2.nifty.com/eman/quantum/creat_op.html
電磁波と光子の関係というのはこのように理解すればいいわけですね。
お久しぶりです。ブラックうールについての質問とは「大きなブラックホールでもトンネル効果によってエネルギーが失われていくのか?」というものでしたね。鈴木さんにご質問いただいたのは2月17日でした。
その後、大栗先生の講義は行われていず、次回は6月2日になります。それまでお待ちください。
あと、可視光線、紫外線、赤外線、γ線などについてですが、これは電磁波と同じです。つまり電場と磁場の振動が空間を伝わっていく現象です。電子が粒として進んでいくのでも、光子が粒として進んでいくのでもありません。
電子が粒として進んでいくものを「陰極線」と言います。ネットで検索すると理解できると思います。ブラウン管テレビの原理ですね。磁場をかけて電子の流れる方向を制御してスクリーン上の光点を移動させて映像として見せるわけです。このときの電子の流れ(陰極線)は電磁波ではありません。
光子についてですが、原子の中の電子がエネルギー準位を変えるときに、そのエネルギー差が光子として放出されると言われています。アインシュタインの光量子説ですね。これを古典的な電磁波(つまり光線=)という考え方をすることはありません。しかし光子というものが粒で存在するのではないという考えの人もいます。ご参考までに以下の記事をご紹介させていただきます。
光子っていらない子?
http://d.hatena.ne.jp/rikunora/20110416/p1
また質問したいことがありますがよろしいでしょうか?
初歩的な質問で申し訳ありませんが光のことです。フォトン(光子)はありふれた素粒子の一つだと思いますが可視光線、紫外線、赤外線、γ線などはやはり電子の物質波と同じく光子の物質波と理解してよろしいでしょうか?もしそうでないときは可視光線などの光子の波動と物質波との関係はどうなるのでしょうか?
ご質問ありがとうございます。とはいいましても、内容は最先端物理学の中のひとつの仮説をもとにしたものですので、素人の私などがご返事できるようなものではありません。
6月に大栗先生の講義に参加する予定ですので、話の流れの中にブラックホールやホーキング博士の話題があれば先生のお考えを聞いてみたいと思います。
今回はブラックホールの疑問点について質問したいと思っています。
有名な科学者ホーキングはミニブラックホールはトンネル効果によってエネルギーを失いすぐ消滅するといいましたが、大きなブラックホールでも同じようにトンネル効果によってエネルギーを失っているのでしょうか?もしそうならブラックホールの内部から何も出てこないというブラックホールの概念に反することになりますが?
また内部から出てくるエネルギーはどのような形で、たとえば光子として出てくるのでしょうか?
お久しぶりです。再びコメントいただき、ありがとうございました。
数学だけでなく、物理学も研究なさっているのですね。初期宇宙の大きさをどのように求めたのかわかりませんが、計算結果を自分で導けるというのは素晴らしいことだと思います。
今年もよろしくお願いします。
訂正コメントありがとうございます。
「n次元のキス数は3x(2のn-2乗)」であれば、次元数が増えるにつれてキス数が膨大に増加していくのと当てはまっていますね。
n次元のキス数は3x(2のn-2乗)です
なるほど。。
ご説明いただきありがとうございました。
次元 キス数
2 3
3 6
4 12
5 24
n 6n
それで等角直線の最大本数と一致するのは各次元で使用した円、球、超球の個数ということになります
コメントありがとうございます。
キス数は以下のように急激に増大しますが、当確直線の最大本数も同様に増大しますか?
次元:キス数の下限と上限
------------------------
1 : 2
2 : 6
3 : 12
4 : 24
5 : 40 - 46
6 : 72 - 82
等しい半径の円、球、4次元以上では超球を
2次元空間(平面)のときは3
3次元空間(立体)のときは4
4次元以上では4+1、4+2、・・・・
の個数のものをそれぞれお互いに接するように配置すればそれぞれの空間のキス数と等角直線直線の最大本数は等しくなります。
お久しぶりです。前回コメントいただいた頃はまだ暑い盛りでしたが、やっと秋らしくなってきましたね。
鈴木さんが研究されている多次元(n次元)の等角直線というのは、多次元空間の正多面体(多胞体)に関係があるのかもしれないなと思いました。多面体の面の中心を垂直につらぬく直線たちは多面体の中心で同じ角度で交わるわけですし。
4次元の正多面体について説明しているページを見つけました。
4次元の正多面体
http://www.geocities.jp/sgwr0/poly4dim/poly4d.html
http://www.interq.or.jp/blue/kawashu/include/i06.html
高次元の正多面体
http://hp.vector.co.jp/authors/VA030421/fdd03.htm
http://eprints3.math.sci.hokudai.ac.jp/364/4/jin0804.pdf
キス数という言葉は初めて聞きました。これから研究してみたいと思います。
等角直線の無限次元の空間と量子力学に出てくるヒルベルト空間と何か関係があるのかなと思っています。等角直線を等角ベクトルとして考えてみたいと思います。
なお私の等角直線の計算は3つの方法で計算できることがわかりました。一つの方法は内積です。この方法は計算がとても複雑になります。三次元まではなんとか計算できました。それ以上はスパコンでないと無理です。
はじめまして。初コメントありがとうございます。
鈴木さんがご提示になった問題は、3次元のときにそのように実際の分子や結晶の構造と符合してくるわけですね。無限次元空間で90度というのも興味深いです。
この問題はだいぶ前に書いた「キス数」の問題と共通していると思いました。(3次元のときは違うかな??)
キス数
http://blog.goo.ne.jp/ktonegaw/e/3fff2b46269846dff3db22e01744d085
これからもよろしくお願いします。
気力で暑い夏を乗り切りましょう!
私はn次元空間において一点で放射状に交わる直線がお互いに等しい角度で交わるときその直線が最大何本あってその場合交わる角度の大きさはいくらになるか計算してみました。
3次元空間について適用するとその数学モデルはメタンの分子模型やダイヤモンドの構造とと同じであることがわかりました。4次元空間の場合そのモデルは何に相当するかまだ解りません
∞次元空間でこれらの直線の交わる角度はちょうど90度になります
長さ0cmのものがあることを「存在している」と見なすのであれば、1次元のときも赤い球体は存在していることになりますね。
0次元のときはいったいどう考えたらいいのか僕も興味がでてきました。
ユニークな発想のコメントをいただきありがとうございました。
ところで「篁」さんのお名前は「たかむら」とお読みするのでしょうか?ネット検索してみたところそのようなお名前の方がヒットしました。何歳になっても読めない人名はあるものですね。
1次元時は赤い球体が入る「隙間がない」じゃなくて「隙間が0cm」で、隙間と赤い球体自体は「存在している」んじゃない??
長さが0cmなだけで。
0次元で青い球体が1つ、つまり「青い球体同士の距離」って概念がなくなるから、そこで初めて赤い球体が消滅…つまり「null」になるのかなっと。
この際、(√n-1)/2の解がマイナスになるけど、適用できる前提なのか、どう解釈すべきか考えてみようかな。
計算方法をもう少し詳しく図解して説明すればよかったですかね。
wachiさんのブログ、これからもちょくちょくお邪魔させていただきますね。
しばらく好天が続くようで何よりです。のどかな日曜日をお過ごしください。
私のような凡人にはわかりましぇん。。。苦笑。
やっぱり頭の構造が違うんだろうなぁ。。。
そんなとねさんが私のような地味~なブログにコメントくださって、ありがとうございます。
これからも諭してやってくださいませ~。
私もちまちまと読まさせていただきますので~。