
平成34年度から実施される予定の学習指導要領について、2月14日から3月15日まで次のページで意見公募が行われている。現在の小学5年生が高校生になるときに実施されることになるはず。
学校教育法施行規則の一部を改正する省令案及び高等学校学習指導要領案に対する意見公募手続(パブリックコメント)の実施について
http://search.e-gov.go.jp/servlet/Public?CLASSNAME=PCMMSTDETAIL&id=185000958&Mode=0
数学 統計関係部分抜粋
http://www.stat.go.jp/teacher/dl/pdf/c3index/guideline/high/math.pdf
統計学習の指導のために(先生向け)「授業モデル」「補助教材」「学校教育における統計教育の位置付け」
http://www.stat.go.jp/teacher/index.htm
今回の記事では高等学校の数学および情報の教科について、思ったことを書いておこう。参考にしたのは上記のページに掲載されている4つのPDF文書、およびその下に載せた統計関係のページ、そして「寺田文行先生の「数学の鉄則」シリーズ」で紹介した1980年代、1990年代の数学の参考書、さらに現在書店で売られている数学の参考書、「学習指導要領の変遷」というページなどだ。
これらの方針を流れる思想は高校だけでなく小学校、中学校の学習指導要領にも適用されるので、それを踏まえて考えることが大切だ。また僕を含めてこのブログをお読みになる方は、自然科学を学ぶには何が優先されるべきかという視点で考えてしまいがちだが、これからの社会を担う子供にとって何が大切であるか、日本全体を活性化するために何を優先すべきかという視点も忘れてはならない。
数学および情報の教科に関して、今回の大きな変更点は次の5つだ。
- 数学の「統計、データの分析」を重視し、内容を充実させる
- 数学Cの復活、「ベクトル」が数学Bから数学Cへ移行、「行列、1次変換」は復活せず
- 数学Aから「整数」が消滅
- 「情報」をプログラミングも含めて文系理系共通で必須科目として行う
- あらゆる教科でコンピュータの活用を推進
全体的に見て「これは詰め込み過ぎだなぁ。」という感想を持った。「ゆとり教育の失敗」への反省が強い反動として表れてしまったかのようである。
どれも確かに重要なのはわかる。数学、情報以外に物理や化学などの科学、国語や社会科系の科目もあるのだから、1980年頃に高校時代を過ごした僕には隔世の感がある。日本を取り巻く社会情勢は変わったし、社会人になって必要なことは増えているのも事実だ。どれも教えておきたいという気持ちはわかるが、授業時間数は昔も今も同じである。どれを捨ててどれを取るか。。。悩ましい問題だ。
あと5つの変更点に色濃くでているのが「国内産業の活性化」、「教育情報化の推進」という国の方針だと思う。基礎的で理論を重視した分野よりも、社会に出てすぐ役に立つ技術的、応用的な分野を重視したカリキュラムとなっている。
数学はI,II,III,A,B,Cに分かれていて、このうち文理共通で必須なのは数学Iだけであるが、通常文系の生徒は数学I,A(+II,B)を、理系の生徒は数学I,II,III,A,B,Cを履修することになる。(注意:現行の過程では数学Cは教えられていない。)
つまり、現実としては次のようになる。
文系の生徒:数学I,II,A,B(または数学I,A)
理系の生徒:数学I,II,III,A,B,C
数学の「統計、データの分析」を重視
「学習指導要領の変遷」のページに「統計」が書かれていないことからわかるように、「統計、データ分析」は少なくとも1980年以降、現在に至るまで一貫して教えられている。1980年頃にも確率分布や仮説検定は教えられていた。しかし、今回の改訂を細かく見ると次の点が重要だ。
- 数学Bに標本調査、確率分布、仮説検定が追加
- 標本調査をコンピュータを使って確認する
- 日常生活、社会生活に対して数理的考察力をつける
これらが文理共通の必須学習項目になったことが最大の変更点なのだ。1980年代にも「理系であっても高校で統計は必要か?」という議論はあったし、2番目と3番目はその時代にはなかった項目だ。
統計やデータ分析はビッグデータの重要性が東日本大震災後の分析で認識されたし、医療や経済、ビジネスでも重要だ。もちろん自然科学でも不可欠だ。文理共通というのはうなづける。
しかし、統計は応用数学の範疇であり、高校レベルの基礎学力では数式の意味(たとえば確率分布)を正確に理解できるはずがない。多項式の積分を学んでいないうちに統計を学ぶのは論理を無視することになり、丸暗記を強いることになる。(統計で学ぶ確率分布関数は積分だ。)あと数学の他の基礎的項目との間のバランスが悪くなる。僕としてはこれら3つは理系専門の項目に移動させるか、2番目と3番目を削除したいところだ。
数学Cの復活、「ベクトル」が数学Cへ移行
数学Cの復活と聞いて喜んだのはつかの間。詳しく見て唖然としてしまった。「ベクトル」が数学Bから数学Cへ移行、そして「行列」は復活しない。ベクトルと行列など線形代数に必要なことは理系専門に押しやられてしまった。文系の生徒は行列や1次変換はおろか、ベクトルさえも知らずに人生を過ごすことになってしまう。
そして理系にしても3年生になってからしかベクトルを学べないし、行列や1次変換を全く学べないのは大問題だ。数学Cを復活させたことの意味が半減してしまう。(1980年頃、僕は高校2年と3年でベクトルと行列、1次変換を学んでいた。)あと、文系の生徒は複素数だけ学んで複素平面は学ばない。これもいただけない。
この件については、ジョゼフ・アンリさん(@joseph_henri)が次の図をツイートされていた。
(引用元)(拡大)
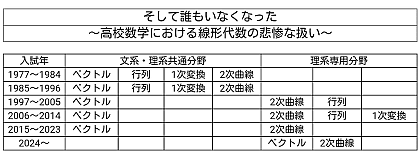
(引用元)(拡大)
「統計、データ分析」を増やした結果、数Bにあった「ベクトル」が復活させたばかりの数Cに入れられた。そしてもともと数Cに入っていた「行列と1次変換」が押し出され、高校数学の外に捨てられてしまったことになる。
「統計、データ分析」と「行列、1次変換」はどちらも大切なことはわかりきっている。しかし、生徒や日本経済の将来を考えるとき、どちらがより重要か?と問われれば、僕は「行列、1次変換」に軍配を上げたい。
文系・理系を問わず、大学で情報系の学部を選択しプログラマ、エンジニアになる人もいる。情報系に大切なのは線形代数(行列とベクトル)や整数だ。この視点に立てば行列とベクトル、整数は文理共通の数学Iあるいは数学Aで履修すべきということになる。情報系にとっても統計の必要性は行列とベクトルよりも低い。
数学Aから「整数」が消滅
「統計、データ分析」を重視したせいで、「整数」が高校数学から追い出されてしまった。整数概念自体は簡単だが、高校数学は「整数問題」のことであり、思いのほか難しい。整数問題に対してのアプローチは他分野とは大きく異なり、独特なものが多いのだ。パズル的要素が大きい分野である。数列とはつながりをもつが、他の分野とは関連があまりないのが追い出された理由だと僕は思っている。
情報、プログラミングの必須化
「情報I」、「情報II」という教科。このうち文理共通で必須なのは「情報I」だ。詳細は次のページをお読みいただきたい。
2020年、次期学習指導要領~情報科:プログラミング教育のほかには?
https://edutmrrw.jp/2017/innovation/0313_2020education
僕はIT業界の人間のひとりとして、現代社会でコンピュータや情報リテラシー、情報セキュリティの重要性はじゅうぶん認識している。(もともと僕はC言語のプログラマーだった。)
この分野が学校の教育課程に組み込まれたのは平成11年度からだ。小中高を通じて「ICT利活用の促進」が行われてきている。
今回の改訂で大きく変わるのは、情報教育、プログラミングが小学校、中学校だけでなく、高校でも文理共通の必須項目になることだ。
情報リテラシーや情報セキュリティについて教えるのを義務化することには、僕は賛成したい。しかし、プログラミングの義務化には反対で、必須項目ではなく文系理系を問わない形の選択項目にしておいたほうがよいと思っている。(つまりプログラミングは情報IやIIとは切り離して科目設定する。)
そして、コンピュータの操作に関して文理共通で義務化するのであれば、文書作成ソフト、表計算ソフト、プレゼンソフトなど事務作業に役立つ範囲で教えるのがよいと思う。プログラミングは興味を持った生徒だけ、必要と感じた生徒だけが選択すればじゅうぶんだ。
まず、プログラミング言語や開発環境、OSを全生徒の授業のために準備するのが大変である。そしてそれらは数年のうちに陳腐化してしまうから、そのたびに教える内容が変わってしまう。変化についていける教師はほとんどいないだろう。外部から先生を呼ぶにしても、全校生徒に対して継続的に教えるのはコストがかかり過ぎる。
そして問題なのはその効果だ。プログラミングを学ぶのは手間のかかることであり、工学系の大学では4年間、専門学校では2年間みっちり学ぶだけの分量がある。小中高を通じて教えたとしても学習時間はどれほど取れるだろうか? 印刷されたプログラム・リストを呪文のように入力して実行したところで、もともと興味のない生徒にはほとんど意味がない。
身の回りにいる大学3年生3人に聞いてみたところ、次のような返事がもらえた。
大学生1(文系男子): 小学校、中学校プログラミングの授業はあったが、まったく覚えていない。
大学生2(文系女子): 高校ではプログラミングをやっていない。やらなくてよいと思う。
大学生3(看護系女子): 小中高でプログラミングの授業を受けたが、まったく覚えていない。必要ないと思う。
理系の生徒、プログラミングが必要だと思う生徒は、放っておいても自分で学ぶだろうし、選択科目としてあれば履修するだろう。問題はプログラミングなど将来絶対に使わないと思っている生徒に強制することなのだ。まかり間違って興味をもつかもしれないのは5パーセントくらい、残りの95パーセントの生徒は、プログラミングが嫌いになるのではと僕は思う。食いつき率が5パーセントあれば上等だと思うという意見もある。
また「情報」は大学入試の科目ではない。コンピュータ科学科や情報科学科であっても、入試科目としては設けられていない。つまり、生徒や高校はおのずと軽視することになってしまうのだ。情報リテラシーや情報セキュリティを徹底したいのならば、大学入試にもそれらを盛り込む必要がある。
あらゆる教科でコンピュータの活用を推進
教育の現場でコンピュータやタブレット端末を使うことに、僕は全面的に賛成だ。優れたコンテンツが開発されることを期待している。
デジタル版だけでも正式な教科書に 政府が閣議決定
2018/2/23 9:56
https://www.nikkei.com/article/DGXMZO2728984023022018CR0000/?n_cid=SNSTW001
地学について(おまけ)
物理、化学、生物と比較して人気がない地学である。僕が高校生のころは今よりも、ずっとマシだったが、地学を選択していた生徒がいちばん少なかったのは事実である。
地震、火山、気象災害が頻発しているのだから、地学をもっと教えなければいけないと思う。学問分野、研究分野としても新しいことがまだまだたくさんある分野である。しかし、他の分野と比較して地学が活発に研究されないのは、お金を生み出す産業に結び付きにくいことがいちばん大きいと思う。天文や宇宙も地学の範疇だが、宇宙開発が経済活性化に還元されるまで待つにはかなりの忍耐が必要だ。
ざっくばらんに、思ったことを書いてみた。みなさんのご意見、お考えをコメント欄、ツイッターにいただけるとうれしいです。
-----------------------------
2018年3月15日に追記:
高校学習指導要領の改訂案がおもしろい
中教審の方針が「統計的内容をもっとやれ」だった
http://webronza.asahi.com/science/articles/2018030500011.html
-----------------------------
2019年5月22日に追記:
2022年度から実施される学習指導要領が決まったばかりであるにもかかわらず、このようなニュースが報道された。
高校の数学に「行列」復活も、国が本腰入れるAI人材教育の詳細が判明
https://tech.nikkeibp.co.jp/atcl/nxt/column/18/00001/02190/?n_cid=nbpnxt_twbn
関連記事:
寺田文行先生の「数学の鉄則」シリーズ
http://blog.goo.ne.jp/ktonegaw/e/412539f939c8058c9b57368f98abce16
復刻版 チャート式 代数学、幾何学(数研出版)
http://blog.goo.ne.jp/ktonegaw/e/412539f939c8058c9b57368f98abce16
大学への数学(研文書院)
http://blog.goo.ne.jp/ktonegaw/e/6124158481ed8d9d4655478643be0db8
学習参考書が電子書籍化され始めている件
http://blog.goo.ne.jp/ktonegaw/e/cdbd82914186c4b8dda69ab77e6efa07
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。




























有意差検定とかは生物・医学系の研究のように効果の白黒をつける場合には便利ですが、漠然としたビッグデータを分析して今まで知られていない傾向・関連などを探索するには多変量解析が必要で、統計ソフトを使わないと実際は無理だと思います。
細かいことをいうと、母集団の分散は n で割るのに対し標本分散は n-1 で割るということを説明するのはちょっとしんどいです。数学好きの人は何で違うかを理論的に知りたいだろうし、嫌いな人は何で二つの方式があるのか分からないだろうと思います。
統計数学をちゃんと理解するには応用数学のしっかりとした知識が必要で、数学科でない限り学校でも検定や推定の方法論しか教えてもらえません。で、そういう手法は使わないとすぐに忘れてしまうものです。
つまり、将来そういう統計学を使う仕事に就きたいと強く考えている人以外は、あまり必要がないと思います。
なので、そういうことを教える時間があるならば、行列などを教えたほうが良いと思います。
私は、会社で品質管理をやっていたこともあるので、統計学の全くの素人というわけだはありません。そういう人間から見ても高校以下の学校で統計学を教えてもあまり効果がないと思います。
プログラミング教育ですが、これも疑問ですね。それなら表計算を教えるほうが有効かも知れません。(VBAを使わなくても)Excel でかなりのことが出来て、プログラミングに繋がる論理的思考も養われると思います。ちょっとしたシュミレーションも工夫次第で実行できるので、理系・文系を問わず便利なものです。プログラムに出来て表計算には実行し難いのは「繰り返し」位だと思います。
ご意見をいただき、ありがとうございました。
有意差検定が役に立つのはサンプルが十分得られない、臨床医学や放射線と癌の発生の因果関係の立証などの分野ですね。多変量解析をビッグデータに対して行うのはT_NAKAさんがおっしゃるように、また別の領域だと思います。
高校生に教えるのなら、昨今話題になった次のことなどがよいと思います。
- 因果関係と相関関係の取違い
- おかしな円グラフや折れ線グラフ、棒グラフ
- 中央値と平均値の違い(たとえば所得分布を使って
表計算ソフトの使い方を教えるのはとてもよいと思います。あとテキスト・エディタで正規表現を使った一括置換で作業を効率化するテクニックとかもよいと思います。
データを加工する事で色々分かると言う経験は進路によらず有益だと思います。
プログラミングは計算機でなくても掃除とか料理の手順を書いて実行すれば繰り返しも条件判断もあって充分だし、具体的で分かり易いんじゃないですかね。
コメントありがとうございます。
データを視覚化して相関をみたり、データを加工して吟味するのはよいですね。
料理の手順作成とか面白そうですね。教材開発の指針は文部科学省が出すのでしょうけど、教材、特にプログラミング教育のためのコンテンツのアイデアは教科書会社の社員が知恵をしぼるのか、そのあたりも下請けに外注されるのか知りたいところです。
現在大学4年で、4月から高校で物理を教えます。専攻は物理教育でした。
ベクトルは数Cに飛ばされるように見えますが、実は必修の物理基礎で力の合成とかで最低限のことは習うんです。だから、僕の中ではベクトルの基礎は物理に押し付けて発展的なベクトルは理系数学に回そうという意図があるんだ解釈しています。
指導をまわされた物理教師としてはたまったもんじゃありませんが、たしかにセンター試験とかで出題されるようなベクトルの細かいこねくり回しが文系に進む人にとってどれくらい必要かと考えると、物理で実例を交えながらベクトルの概念を理解する程度でもいいのかなとは僕は思います。
はじめまして。ブログをお読みいただき、ありがとうございます。
この記事を書いたとき、物理のことはすっかり失念しておりました。力の合成や分解は高校物理の力学で大切ですね。ベクトルの基本です。
高校数学でベクトルが重要なのは直交座標との関係、平面ベクトル、空間ベクトル、そして内積がひとつ。そして行列と1次変換だと思います。
文系の人にとって将来どのような分野でベクトルが必要になるか考えてみると、3DやAIを扱うプログラミング、経済学、多変量を扱う統計処理などがあるかもしれません。しかし、必要になったときに学べばよいことですね。
4月からの教師生活、頑張ってください!未来担う若者を育てる仕事っていいですね!
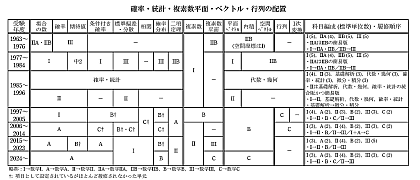
私の作った図を使っていただいて感謝しています。書いた私が言うのもあれですが,1枚目の図なんて電車の中でスマホで15分で書いた表がバズったのは衝撃的でした。
前置きはさておき,統計押しなのはいいんですが,現行課程ですら数学Bで初出のΣ抜きに数学Iで分散・共分散・相関係数や,V(X)=E(X^2)-(E(X))^2を扱っているなど,履修順序がおかしなことになっている感は否めないですね。現行課程・新課程の学習指導要領を見てみると,履修順序や数学的厳密性を無視してまで統計をねじ込んでいる印象はありますね。
# Σを習っていない高校1年生に,分散の定義式をΣを使って書いて慌てて黒板消しで消すという作業は何度もやりました。
更に,大学・大学院で情報工学を専攻していた身として,中学校・高等学校でプログラミングを扱うというのはもっと頭をかしげざるを得ないですね。
大学の理工学部の情報工学科の場合は数学もプログラミングも抵抗のない人間が集まり,教授・准教授という超一流の能力を持っている人に教えてもらうに対し,数学が苦手な人が混ざっている中学生・高校生全員にプログラミング経験のない教員が教える意義は本当にわからないですね。CなのかC++なのかJavaなのかはわかりませんが,教育現場は大混乱必至でしょうね。
とりとめのない文章で失礼しました。
はじめまして。こちらこそ図版を引用させていただき、ありがとうございました。
ジョセフ・アンリ様のツイートがバズったのも、この問題に対する関心がとても高かったことと、図版がとても分かりやすかったからだと思います。文部科学省から公開されているPDFファイルを細かくチェックするのは大変なことですから。
私は教育業界に身を置いたことがありませんから、中学・高校で何をいつ学んだかということはうろ覚えのところがあります。だとしてもベクトル・行列、統計の優先順位はわかりますし、プログラミング教育をすべての生徒に教える必要がないとも思っています。それぞれの学年での学習内容を表にしていただいたこと、現在と次期を比較することで今後どのようになっていくかが非常によくわかりました。
優秀な生徒は自力で学べますが、それ以外の一般的な学力の生徒が特に重要だと思います。次期学習指導要領で学ぶ生徒が、将来どのようになってしまうか、彼らが大学へ進学し、社会に出るときにどのような影響があるかがとても心配です。
これからもよろしくお願いいたします。
現代文などにも言えることなのですが、役に立つ応用分野を詰め込むために教養となる基礎分野を犠牲にするのはこの国の学問の価値を脅かす愚策としか思えません
そもそも、人間が情報処理でAIに太刀打ちできない以上、AIから出てきた情報をどう活かすか考えるための基礎力が重要だと考えられます。ですから、長い目で見ればブログ主さんと同じように統計ではなくベクトルや一次変換といった概念を身につけるべきだと思います
コメントありがとうございます。現役高校生の方からご意見をいただき、心強いです。(鉄則をお使いになっているのですか!)それにしてもしっかりした文章をお書きですね。感心しました。
> 人間が情報処理でAIに太刀打ちできない以上、AIから出てきた情報をどう活かすか考えるための基礎力が重要だと考えられます。
おっしゃるとおりです。
2022年度から実施される学習指導要領が決まったばかりなのに、つい先日次の報道がなされましたね。「行列復活」はうれしい知らせではありますが、相変わらず教育方針がぶれまくっていることに変わりはありません。
高校の数学に「行列」復活も、国が本腰入れるAI人材教育の詳細が判明
https://tech.nikkeibp.co.jp/atcl/nxt/column/18/00001/02190/?n_cid=nbpnxt_twbn