高校の物理の授業で「物体の全質量は大きさのない質点にすべて集中しているものとして計算を行う。」というニュートン力学の大前提に疑問を持った方も多いと思うが、一昨日の「僕が物理と数学にハマリだしたきっかけ - 重心と質点の話」という記事でこの問題を取り上げた。今日の記事はこの大前提を検証してみようという試みだ。
この前提は証明されていない「定理=決め事」である。そしてこの前提のもとニュートンの万有引力は次の式であらわされる。
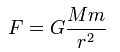
けれども実際のところ、この場合の2つの天体はそれぞれの天体を構成する物質の部分部分がすべて引き合っているわけなので、その微小な引力の総和がこの万有引力の式に一致することは積分計算して確かめてみないと質点はいつまでも「定理」のままである。
ネット検索してもこれに触れているページは見つからなかったので自分で計算式をたてて確かめてみることにする。
2つの天体を両方とも大きさのある物体とみなすと6重積分になってしまうので「地球」と「人間」にとり人間の大きさは無視できるほど小さいという前提条件をつけた。そして人間は地表から h の位置に置いて計算することにした。図で示すとこのようになる。(実際は円はなく球だ。)
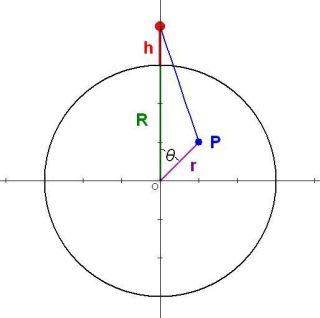
R が地球の半径、点Pが積分のための微小体積要素で地球内部すべてに渡って3重積分する。微小体積要素 P と人間(赤点)の距離の2乗に反比例して引力は弱まることを掛け算する係数として忘れないようにしておく。また一般に微小体積要素 P は人間を斜め方向に引っ張るから引力は地球の中心方向の成分だけを計算して加えるように注意する。
まず、比較のためにこの条件で地球の質量が質点に集中しているとしたときの引力 F の大きさを示しておこう。上記の万有引力の式にこの図の条件を入れると次のようになる。ρは地球の質量密度で地球全体に渡って一定とする。G は万有引力定数だ。m は人間の質量(=体重)とする。
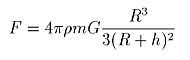
次に地球の全質量が質点に集中するという前提を取り払い、地球を構成する微小体積要素の積分で万有引力を計算してみよう。
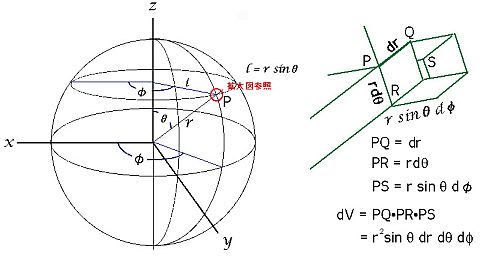
掲載画像のように3次元(立体)の極座標を使って r, θ, φ のパラメータで計算式をたてる。3次元の極座標の詳細はこのページを参照してほしい。計算式をたてる過程で三角関数の余弦定理を2度使い、結果の式はこのようになった。この式ははじめて見る人も多いと思う。

この3重積分を r, θ, φ の変域で定積分すれば、上の万有引力の値と一致するはずなのだが。。。。とても難しくてこんな式は解けない。僕は大学で数学を専攻したが、こんなに難しい積分は見たことがない。微分と違って積分はパズル的要素があるし、どんなに工夫しても解けるはずがない積分というのはかなり多いのだ。(ちなみにこの式のいちばん内側のdrの積分をMaximaを使って解かせようとしたらこうなった。)
ところで「僕が物理と数学にハマリだしたきっかけ - 重心と質点の話」の記事では人間の足元の地面の微小体積要素は人間への距離がゼロなので引力は無限大に発散してしまうのではないかと心配した。これを検証するために積分の中身にこの条件を代入してみる。
人間が北極点に立っていると仮定して h = 0, r = R, θ = 0 を代入すると分母と分子がともにゼロとなり、足元の微小体積要素だけの引力は「不定」となっている。分母だけがゼロだと確実に引力は無限大に発散するが「0/0=不定」になったということは足元の部分の引力は値はわからないが有限の値になるということだ。分母と分子が0になろうとするオーダー(勢い)はともに3乗で効いているから、足元の部分の引力は有限の値に落ち着くことはほぼ間違いない。
とりあえず地球全体の引力は無限大に発散しないですみそうだ。これがわかっただけでも計算式をたてた甲斐があったかもしれない。
次に極座標をやめて、x, y, z の直交座標でも式をたててみた。地球を無限小の立方体に分割して積分をするのだ。引力の3重積分はこうなった。
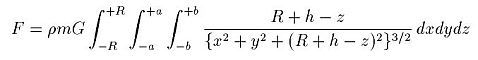
ただし

式はこちらのほうが簡単に見えるが、積分の変域にx, y, zの変数が入っているのでこれもまた難しそうだ。
こちらの式にも h = 0, r = R を代入して人間の足元で引力が発散しないか調べてみよう。実際の値を計算するとやはり極座標で計算したときと同様0/0になって「不定」になっている。
積分自体は極座標にしろ直交座標にしろ、とても解析学的に文字式の計算で解ける問題ではないことがわかった。(予想通りだけど。)
疑問を解決するには、やはりパソコンでプログラムを組んで数値計算で解くしか手はないかもしれない。このままでは「理科復活プロジェクト」どころか「理科滅亡プロジェクト」になってしまう!
どなたか上の積分のどちらでも構わないので、解ける方がいらっしゃったら教えてほしい。
この話は次の記事につづく。
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。























