
素粒子の数式(標準理論の数式)
番組を見た人も、また見れなかった人にもより深く理解していただけるように解説記事を書いてみた。
キーワードをメモしながら番組をもう一度見て文章として書き起こした。それから僕の解説を緑色の文字で挿入したのが以下の文章である。
YouTubeで再生: 1回 2回 完全版(4回シリーズ)
YouTube: 動画検索
今回の記事は短縮版2回シリーズとして放送されたものを解説した。完全版4回シリーズの解説は「番組の感想:NHK-BS1「神の数式 完全版」」として書いている。短縮版と完全版の対応関係は次のようになる。
短縮版第1回: 完全版第1回と第2回
短縮版第2回: 完全版第3回と第4回
「神の数式」第1回:この世は何からできているのか
NHKオンデマンド: http://www.nhk-ondemand.jp/goods/G2013051400SA000/index.html?capid=mail_131018_c001_B_11
まず番組冒頭で鉛筆を立てようと頑張る子どもたちの映像が映され、この「鉛筆が倒れる」という現象が科学的大発見のきっかけになったことが伝えられる。それはいったいどういうことなのか?
余談: 鉛筆を立てようとする試みについては、後日「鉛筆はどれくらいの時間立っていられるか?」という記事で解説したので、寄り道がてらお読みいただきたい。
次に昨年の夏、CERNで報告されたヒッグス粒子の発見の様子が紹介される。これは世紀の大発見でこの素粒子は「最後の素粒子」なのだという。
倒れる鉛筆とヒッグス粒子、この2つを結びつけるものは「自発的対称性の破れ」という理論で、2008年にノーベル物理学賞を受賞した南部博士による着想だった。創造主はどのような設計図をもとにしてこの宇宙を作り上げたのか。神の設計図は数式であらわされていると物理学者は信じている。
解説:2008年にノーベル物理学賞を受賞したのは、南部博士の他、小林博士、益川博士だ。小林・益川理論は「CP対称性の破れ」というもので、今回の番組では紹介されなかった第2世代、第3世代のクォークの存在を予言した。結局これらのクォークも発見され、素粒子の標準理論で、クォークは6種類あることになる。
近年、神の数式に肉薄する数式が求められ、一応の成功をおさめたのだという。その数式を使えばオーロラの現象、大気の動き、電気のかかわる現象などを説明できるそうだ。もしあらゆる現象を寸分の狂いもなく表すことができたら、それは神の数式といえよう。それは万物の理論であり素粒子から大宇宙までのすべてを説明できる。
解説:万物の理論は「基礎物理学」と呼ばれている分野であり、素粒子から大宇宙までの物質やエネルギー現象をすべて解き明かすことが目標だが、これが達成できても「全て」が解明されるわけではない。たとえば複雑な生命現象や人間の感情や思考、社会現象、経済現象など因果関係が複雑にからみ合う世界は基礎物理学だけでは解明できない。当たり前のことだけれども、一応述べておこう。
この番組では完璧な美しさをもった数式を求めるために、100年に渡る物理学者たちの苦闘を紹介する。その過程でこの世は数式上存在してはならないという驚くべき結論が導かれ、苦悩の時代が続いたこともあった。そして南部による「鉛筆のアイデア」がその突破口となる。それによると「完璧な美しさは崩れる運命にある」のだという。
第1回は「この世界は何からできているのか」と題した素粒子物理学の発展史だ。
物理学者は、いつも数式のことばかり考えているちょっと変わった人たち。彼らがどんな方法で万物の理論に肉薄しようとしてきたのか、そして彼らはついにその神の数式にかなり近づいたというのだ。
CERNの裏庭の大きな石にその数式は書かれている。これが物理学者が到達した素粒子の「標準理論」の数式だ。
解説:この記事の冒頭に掲載したのが数式の書かれた大きな石だ。そしてこの回ではこの数式の解説を上から順番に行う。

数式の2行目から4行目に書かれているのはこの世界で働いている「力」をあらわし、それぞれ電磁気力、弱い核力、強い核力と呼ばれている。
物質を構成する素粒子については4種類あり、電子、ニュートリノ、アップクォークとダウンクォークである。これらは素粒子の理論では「第一世代の素粒子」と呼ばれている。
解説:物理学ではこれ以上分割することのできない基本的な粒子のことを総称して「素粒子」と呼んでいる。第1世代、第2世代、第3世代、そして昨年発見されたヒッグス粒子を含めて「標準理論」に含まれる素粒子は次のように17種類ある。番組ではその一部(第1世代のクォーク、ニュートリノ、電子と光子)だけが紹介された。
クリックで拡大
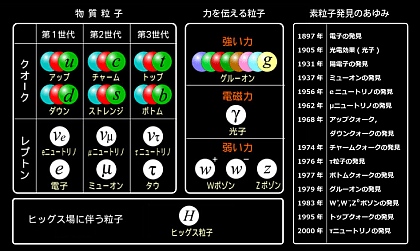
視点をミクロの世界に移す。すると原子は原子核のまわりを回る電子、そして原子核には陽子と中性子が含まれ、それらはクォークで構成されている。そしてときおり原子核の中からニュートリノが飛び出してくる。これらの粒子はそれぞれ電磁気力、弱い核力、強い核力で相互に結びついていて、物理学者たちはこれらの力からすべてを説明できると信じているのだ。そして数式の5行目に書かれているのが最後の粒子として昨年見つかったヒッグス粒子をあらわしている。
解説:陽子はクォーク3個、中性子はクォーク3個、中間子はクォーク2個によって構成されている。ヒッグス粒子は1964年にその存在が予言され、2012年7月4日にその発見が発表された。
さて、この数式の1行目から説明しよう。1行目は電磁気力をあらわす数式だ。1920年代後半、イギリスのケンブリッジ大学で研究をしていたポール・ディラックという物理学者がいた。彼は30歳にして同大学のルーカス教授職という地位につく。これは過去ニュートンやホーキング博士が就いた名誉ある地位である。
ディラックは特に「数式の美しさ」にこだわっていた。その当時、素粒子はまだ電子しか見つかっていず、それがマイナスの電気を帯びていることがわかっていた。また電子はこの時代に見つかったばかりのシュレディンガー方程式に従って運動していることがわかっていた。しかし、この方程式を使っても解明できない問題が残っていた。それは電子のエネルギーについて、電子が自転(スピン)について、電子が磁石のような性質をもっていることなどの問題だ。なぜ自然はそのような性質を電子に与えたのか?物理学者たちはその数式を求めたがまったく歯が立たなかった。
それまでの物理学者たちは実験や観測結果を数式に置き換える方法をとってきた。けれどもディラックの方法はそれとはまったく違い、「物理法則は数学的に美しくなければならない。」という自分の美的感覚にしたがって数式を導くものだった。「美しさ」は人によって違う曖昧な概念だ。しかし物理学者たちが考える「数学的な美しさ」ははっきりとしている。それは「数式が対称的である。」ということなのだ。
たとえば「円」の数式を考えてみよう。中心を軸として円を回転させても数式の形は変わらない。これは「円の数式は回転対称性を持っている。」という意味である。次に平行に並ぶ縞模様の上の図形を考えてみる。図形を平行移動しても数式の形は変わらない。これが「並進対称性を持っている。」という意味だ。
ところが円を平行移動させると、円の数式は形を変えてしまう。これは「円の数式は並進対称性を持っていない。」ことを意味している。つまり「対称的」というのは「見る人の視点が変わっても性質が変わらない。」ことであり、それは「視点が変わっても数式の形が変わらない。」ことなのだ。
対称性にはこのほか「ローレンツ対称性」というものがある。これはアインシュタインが導いた特殊相対性理論によると「時間と空間は同じもの」という解釈がなりたち、つまり4次元時空の対称性をあらわしているものだ。
ディラックが研究のもとにしたのはミクロの世界の素粒子で成り立っている「シュレディンガー方程式」である。この数式には時間をあらわすtが1つ、空間をあらわすxが2つ書かれている。つまり時間と空間は同等に扱われていないので「ローレンツ対称性」はもっていない。
シュレディンガー方程式
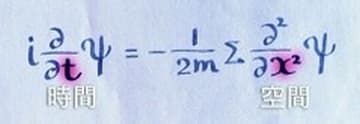
解説:シュレディンガー方程式は偏微分方程式と呼ばれている数式に分類される。微分を行なう回数のことは「階数」と呼んでいる。けれども一般視聴者向けの番組なので「階数」のことを「個数」と表現したわけだ。
ディラックは電子のもつ「回転対称性」と4次元時空が満たす「ローレンツ対称性」を同時に満たす数式を探し求め、ついにひとつの数式にたどり着く。苦労は報われた。この数式にはtとxがひとつずつあるのでローレンツ対称性をもっていることがわかる。そしてこの数式によって電子が自転(スピン)していることと、磁気(磁気能率)をもっていることの説明がついたのだ。

解説:ディラックの電子の理論はミクロの世界の現象を説明する「量子力学」とアインシュタインが1905年に発表した「特殊相対性理論」を統一した「相対論的量子力学」という理論だ。これによって上記のような電子のもつ2つの性質のほか、陽電子の存在が予言された。陽電子とはプラスの電荷を帯びた電子のことで、電子の反粒子である。陽電子はディラックが予言した4年後の1932年にアンダーソンによる実験で発見された。つまりディラック方程式を含んでいる素粒子の数式は上記の素粒子だけでなく反粒子、反物質のことも含んだ数式なのである。
参考記事:ディラックによる陽電子の予言(1928年)
https://blog.goo.ne.jp/ktonegaw/e/0764eaa33a765ffff27bccee3e35b4f3
ディラックの量子力学(相対論的量子力学)は、ディラックみずから書いた教科書(原書第4版)として1963年に完結し、その日本語訳は1968年に刊行、2017年に改訂版が刊行された。陽電子の存在を理論的に導出した名著である。(陽電子の存在を記述したページはこの記事でご覧いただける。)
発売情報: ディラック 量子力学 原書第4版 改訂版
https://blog.goo.ne.jp/ktonegaw/e/19193db48c2ca3c17c9422d1827de6d4
晩年のディラック博士による量子力学の講義(Paul Dirac: 1902-1984) 動画は途中から安定します。
1982年、ゲッティンゲンでのインタビュー
このようなわけで素粒子の数式の1行目には「ディラック方程式」が書かれている。これは物理法則において「対称性」がいかに大切かを印象づけ、物理学者の研究方法に大きな影響を与えることになった。
しかし、まだ3つの力の数式がわかっていない。まず電磁気力である。これは原子どうしを結びつけている力だ。電磁気力の数式に挑んだのがオッペンハイマーである。彼は「原爆の父」として知られているアメリカの物理学者だ。
解説:電磁気学は1864年にマックスウェルによって「4つの数式」で表わされることが示された。けれどもそれは電子の発見の前のことである。電気を帯びた粒子どうしの引力や斥力(反発力)すなわち「クーロン力(=電磁気力)」が万有引力と同様に、逆2乗則に従っていることがこの数式で示されていたが、「クーロン力」がどのように発生するかはわかっていなかった。(マックスウェルによる電磁気学の数式が発表された頃のアメリカは南北戦争の時代、日本では坂本龍馬が活躍し池田屋事件がおきていた。)
オッペンハイマーとディラック、そしてシュウェーバーの3人は電磁気力に対して成り立つ新たな対称性を求めることに成功した。それは「ゲージ対称性」と呼ばれるものだ。ゲージというのは「物差し」のことである。番組では目盛のついた円形の分度器が紹介される。左右のどちらに回転させても数式の形は変わらない。それではゲージ対称性は何が回転するのか?難しいことはともかくディラック方程式の発展版とお考えいただきたい。
解説1:分度器は左に40度回してから右に60度回すと結果は1回の回転として右に20度回転させたことになる。右に60度回してから左に40度回しても結果は同じである。これは回転操作の順番を変えても結果が同じ、つまり複数回の操作の順番が「可換」であることを示している。この3人が求めた対称性を厳密に表現すれば「可換ゲージ対称性」というわけなのだ。
解説2:では「何が回転しているのだろうか?」この番組では省略されていたことだ。実際に回転しているのは現実世界に実在する何かではなく、電磁気力の数式であらわされる「数学的な量」なのである。この量はミクロの世界で成り立つ量子力学の波動関数としてあらわされる複素数の量なので、現実の世界のどこかにある(見えたり、観測できたりする)量ではないのだ。詳しいことは量子力学で学ぶ内容だ。この数学的な量の「非存在性」は量子力学の基礎方程式である「シュレディンガー方程式」に含まれている虚数「i」によって象徴されている。
これが素粒子の数式の2行目である。この数式の意味は電磁気力をあらわしている。電子は光子を放って原子核に到達する。原子核と電子はこのように光子をやり取りすることで結びついているのだ。これが電磁気力がおきるしくみなのだ。ここで大切なのは「力は粒子が伝達する」ということである。
解説:原子核と電子の間で光子が交換されることによって逆2乗則に従う電磁気力が伝達されることを、数式で確認したい方は次のページから始まる一連の記事をお読みになるとよいだろう。
Note289 スカラー光子とクーロン力に関する疑問
http://blogs.yahoo.co.jp/cat_falcon/33510875.html
ところがこの数式には重大な欠陥があることが見つかった。オッペンハイマーの1930年の論文によって明らかにされたことは「電子のエネルギーが無限大になる」ということだった。もちろん電子のエネルギーは有限だから現実とは矛盾する。無限大のエネルギーを認めてしまうとこの世界に物質は存在してはならないことになってしまう。
その後、第二次世界大戦に突入し、物理学者の研究は兵器開発に向けて行なわれるようになった。ウランの核分裂の連鎖反応が成功し、アメリカ中から物理学者がロスアラモスに集められた。原爆を開発するための「マンハッタン計画」を遂行するためである。この計画のリーダーに任命されたのがオッペンハイマーだった。開発された原爆は広島と長崎に投下され、数十万人の命を奪った。
解説1:原爆や原子力発電のエネルギーとして使われるのが「強い核力」である。しかしこの時代にはまだ電子のエネルギーが無限大になるという矛盾がまだ解明されていなかった。核力の存在を予言したのはアインシュタインの特殊相対性理論であり1905年に発表された。有名なE=mc^2という数式である。
解説2:「弱い核力」とはセシウムやヨウ素などの放射性物質からでてくる「放射線(電磁波)」のことである。
原爆のもたらした多大な犠牲に衝撃を受けたオッペンハイマーは、その後研究生活から距離をおくようになる。そのような彼のところに1通の手紙が届いた。敗戦国日本から届いた朝永振一郎という物理学者からの手紙だった。
朝永によると電子の無限大のエネルギーという矛盾を解決する方法が見つかったのだという。甚大な戦争被害を受けた日本で物理学の研究の続けることは並大抵のことではない。空襲で焼け落ち、物資にも事欠く東京で朝永はチームを率いて研究を続けていた。自らが甚大な被害を与えた敗戦国日本で、このような日本人がいて世界に引けをとらない最先端の研究成果を上げていることにオッペンハイマーは非常に驚き、すぐさまその論文を英語で送るように朝永に求めた。朝永の英語論文はオッペンハイマーの協力によって、世界的に有名な物理学論文誌「フィジカル・レビュー」に掲載された。
朝永の発表したこの論文は、電子のエネルギーについて特殊な計算方法を使うものだった。この方法を使うと電子の磁気能率が精度10桁という驚異的な正確さで求められ、実験結果を一致することが確認されたのだ。この特殊な計算方法は同じ頃、物理学者ファインマンやシュウィンガーによっても発見されていた。そして3人は1965年にノーベル物理学賞を共同受賞した。
解説:朝永、ファインマン、シュウィンガーによって考案されたこの特殊な計算方法は「繰り込み理論(くりこみ理論)」と呼ばれている。数式上、無限大に発散してしまうエネルギーなどの物理量から無限大の数値を差し引くことで有限の値にしてしまう奇抜な方法だ。3人の計算方法はそれぞれ異なっていたが、後に物理学者ダイソンがこれら3つの計算方法が数学的に同等であることを示した。繰り込み理論によって「相対論的量子力学」と「電磁気学」を統一した「量子電磁力学(QED)」が完成した。朝永先生や繰り込み理論については次のページをお読みいただきたい。
朝永振一郎博士とその業績
http://www.kahaku.go.jp/exhibitions/tour/nobel/tomonaga/p1.html
この成果によって電磁気力の矛盾がすべて解決し、神の数式の2行目が完成した。電磁気力がもつのは「ゲージ対称性」という性質である。
次は神の数式の3行目と4行目、つまり弱い核力、強い核力やそれらの力を生み出す「力の粒子」についての話である。
舞台は1950年代の北京にうつされる。この話の悲劇の主役となるのは物理学者のヤンだ。彼は強い核力と弱い核力の数式を追い求めていた。彼がよりどころにしていたのはもちろん「対称性」である。苦難の末に彼はひとつの数式にたどり着いた。この数式はゲージ対称性の発展形であり「非可換ゲージ対称性」という超難解なものだった。1954年にヤンはこの数式を「荷電スピンの保存とゲージ不変性」という論文で同僚のミルズと一緒に発表する。この対称性は電磁気力のゲージ対称性をヒントにしたもので、さらに素晴らしい美しさをもっていた。
解説1:番組では「非可換ゲージ対称性」の説明が省略されていた。電磁気力で成り立つ「(可換)ゲージ対称性」が円形の分度器を使って説明されるのであれば、「非可換ゲージ対称性」は目盛のついた球形の分度器(地球儀)で説明できる。球のような立体は任意の軸を中心にして回転させることができる。たとえばX軸を中心にして右方向に90度、Y軸を中心にして右方向に90度回転したときと、Y軸を中心に右方向90度回転してからX軸を中心に右方向90度回転したときでは最終結果が違うことがわかる。複数の回転操作を行うとき、その順番によって結果が違ってくるのだ。これを操作が「非可換」であると言う。「非可換ゲージ対称性」はこのように説明できる。
解説2:それでは「非可換ゲージ対称性」では、何が回転するのだろうか?これについても電磁気力のゲージ対称性と同様、この世界に実在する何かが回転するわけではない。強い核力や弱い核力の数式に含まれる複素数の変数に対して「数学的な回転操作(つまり変換のこと)」を行なうという意味だ。この回転を行なっても数式の形がかわらないので強い力や弱い力は「非可換ゲージ対称性」という性質を持っているわけなのだ。
このように「数学的な操作」といってもピンとこない方が多いと思う。そのような方のために日常的な「カップラーメン」の例で説明をしてみよう。(カップラーメンを食べるのを日常的と呼ぶのはさびしい生活のようにも思えるが。。。)
カップラーメンは熱湯を注いでから食べるのが普通だ。「熱湯を注ぐ」という操作の次に「麺を食べる」という操作を行なう。操作の順番を変えると結果が異なってくることは明白だろう。つまりこの2つの操作は「非可換」なのである。このように考えると身の回りには非可換な操作がたくさんあることがわかる。たとえば自動車の「アクセルを踏む操作」と「ブレーキを踏む操作」も非可換な例といえる。
ヤンとミルズが提唱した「非可換ゲージ対称性」は弱い核力に対する非可換ゲージ対称性と強い核力に対する非可換ゲージ対称性の2種類ある。僕の説明では「球の回転」によって説明したが、実際にはそれぞれ複素数を座標軸にもつ多次元空間にある「超球」の回転によってあらわされている。想像しにくいと思うが。。。
解説3:素粒子の数式に示されている弱い核力を伝えるのは「2種類のWボソン」や「Zボソン」と呼ばれる素粒子だ。強い核力を伝えるのは「グルーオン」と呼ばれる素粒子である。番組では紹介されていなかった。
ところがこの数式には予想外の落とし穴があった。この数式によれば力を伝える粒子の重さがゼロになってしまうのだ。光子の重さがゼロであることは昔から知られていた。また、原子核の中で力を伝える粒子は、当時はまだ見つかっていなかったが、それらの粒子が「重い」ことはわかっていた。この予想外の結果はヤンにとっても難問で、ついに彼は数式の完成をあきらめてしまう。
解説:番組では「重さ」と表現していたが、正しくは「質量」である。「重さ」は重力の働いている場所ではプラスの値だが無重力空間ではゼロになる。「質量」は物の動かしにくさをあらわす量で重力が働いていようが無重力空間であろうが変化しない。光子の質量がゼロであることはアインシュタインの特殊相対性理論によって説明される。
その後、ヤンの数式に従えば力を伝える粒子だけでなく、すべての素粒子の重さがゼロになってしまうことが指摘された。つまり、素粒子の重さがゼロになるとそれらは光速で飛び散ることになり、この世界はばらばらに飛び散ってしまうことになる。
この「重さの謎」の解決は自発的対称性の破れやヒッグス粒子の発見まで待たなけらばならなかった。
クォークの重さの謎を解決したのは南部陽一郎だった。彼が2008年にノーベル物理学賞を受賞したのは「自発的対称性の破れ」という理論でクォークの重さの謎を解明したことによる。彼は異質の天才だった。
南部の理論によると、この世界の設計図が回転対称的なものであっても、つまり数式に対称性があっても、そこから導かれる実際の世界の現象には対称性がなくてもよいということだ。
番組冒頭で紹介した「立てた鉛筆が倒れてしまう例」がそれである。数式に従えば立てた鉛筆は回転対称なので倒れることはない。しかし現実には倒れてしまう。これが南部の考えた自発的対称性の破れというものだ。
解説:このあたりの説明は難しいと思う。次のページの解説を参考にしてほしい。
~ 自発的対称性の破れとは ~
https://www2.kek.jp/ja/newskek/2008/novdec/SSBD.html
「自発的対称性の破れ」と南部理論
http://www.sci-museum.jp/files/pdf/exhibit/sbs&nambu.pdf
この考え方は1961年に「超伝導についての論文」として発表された。これによって強い核力の設計図(素粒子の数式の3行目)が示され、クォークが重さを持つことの理由が解明されたのだ。
電子とニュートリノの「重さの謎」についてはヒッグス粒子によって解明された。アメリカの物理学者ワインバーグは1964年に予言されたヒッグス粒子というこの世には存在しない都合のよい粒子を素粒子の数式に導入して電子とニュートリノが重さをもつことの説明に成功した。
ワインバーグによると、この宇宙が誕生したときにはまず真空があり、その後ヒッグス粒子が勝手に増え始めて空間をびっしり埋め尽くしているのだという。その中を電子が運動するとき、ヒッグス粒子による抵抗を受けて進みにくくなる。進みにくいということは重さとして私たちには観測される。これが電子の重さだというのだ。この理論は1967年に論文として発表された。
解説:ヒッグス場の中を抵抗を受けながら電子が進むという説明は誤りである。かといって他に日常的なたとえ話でうまく説明することができないのが苦しいところだ。
ところがこの理論の評判はよくなかった。ヒッグス粒子の仮定があまりに都合よいものと受け取られたからだ。さらに理論としての美しさがないのだという。
それでもヒッグス粒子は予言から40年後の2012年に発見された。これが素粒子の数式の5行目の完成であり、数式全体として標準理論と呼ばれるものなのだ。これが現在「神の数式」にかなり近いものだとされている。
解説1:ヒッグス粒子発見の報告については、次の記事を参考にしていただきたい。
祝!:ヒッグス粒子発見
https://blog.goo.ne.jp/ktonegaw/e/f88350541542f732fec74af583a29e50
解説2:素粒子の数式の左辺に書かれているLはラグランジアンと呼ばれている量だ。ラグランジアンは「解析力学」という分野で学ぶとても重要な物理量だ。とはいえこの説明をすると30分くらいかかるだろうから、省略されてしまうのは無理もないこと。解析力学はニュートン力学から超弦理論まで、すべての物理理論で成り立っている普遍的な原理である。
解説3:「標準理論」に含まれる17種類の素粒子は私たちにとっては別々のものに見えているが、これらの素粒子は数式であらわされる「対称性」という抽象的な世界で美しく結びついていることが明らかになったのである。
宇宙はビッグバンと呼ばれる大爆発によって誕生したとされる。誕生直後の宇宙は設計図どおりの対称性をもち、あらゆるものに重さはなかった。その後、自発的対称性の破れによって重さが生じる。つまり物質ができ、星間ガスから恒星が、恒星が集まって無数の銀河ができた。物理学者たちは神の数式が求められれば、この世界に説明できない現象はないと信じている。
現在、物理学者たちはその先を目指し始めている。すでに求められた素粒子の数式には万有引力のもととなる重力が含まれていない。素粒子は非常に軽いので、これまでの数式では重力を考える必要がなかったのだ。
解説:素粒子物理学では重力を伝達する「重力子(グラビトン)」の存在が予言されている。しかし重力子は朝永先生らによって導かれた「繰り込み理論」をつかって計算しても、無限大の問題を解決することができない。重力理論は素粒子の数式と相性が悪いのだ。
ところでブラックホールの中心の重力はとてつもなく大きく、周囲の空間を大きく歪めてとても小さな世界に圧縮している。この場所では素粒子の数式と重力の数式、つまり「一般相対性理論」の両方が成り立つ数式が成り立っていなければならない。この2つの理論が統一されれば電磁気力、弱い核力、強い核力、重力という4つの力がひとつの数式に統一されることになる。物理学者は現在も4つの力の統一へ向けて研究を続けているのだ。
第2回放送ぶんの解説記事につづく。
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。




関連記事:
番組告知:NHKスペシャル「神の数式」(9月21日、22日)
https://blog.goo.ne.jp/ktonegaw/e/1a809c46b31c32b3b3c84dc0be881ddc
NHKスペシャル「神の数式」の感想
https://blog.goo.ne.jp/ktonegaw/e/a2368bbcee58771d16dbcb4613dc077d
強い力と弱い力:大栗博司
https://blog.goo.ne.jp/ktonegaw/e/06c3fdc3ed4e0908c75e3d7f20dd7177
「標準模型」の宇宙:ブルース・シューム
https://blog.goo.ne.jp/ktonegaw/e/25297abb5d996b0c1e90b623a475d1aa
鉛筆はどれくらいの時間立っていられるか?
(「神の数式」番組冒頭の鉛筆を立てる問題を計算してみよう。)
https://blog.goo.ne.jp/ktonegaw/e/448a4abf90b7f8991e4a3600f2f6535e

























一番下がヒッグス自己相互作用でその上の第一項がフェルミオンとヒッグスの作用、肝心のゲージ場に質量を与えるヒッグス相互作用はh.c.でしょうね。
コメントありがとうございます。
そうです。この数式の意味はまさにそのとおりなのです。
番組の時間の制約上、グルーオン場やフェルミオンとボソンの区別の説明は省略されてしまいましたけど。
原注の中に(i-m)Ψ=Ο
という数式がありました。
声に出して読む場合、何と読んだらいいのでしょうか?調べてはみたのですが…
お教えいただければありがたいです。
音読する場合は「開きカッコ、アイ 引く エム、閉じカッコ イコール ゼロ」と読むのだと思います。
Ο の文字にギリシャ文字のオミクロンを書いていらっしゃいますが、数式の意味から判断すると、これはオミクロンではなくゼロだと思います。