ディラック 量子力学 原書第４版

----------------
2017年11月に追記：

改訂版が刊行されたので、こちらをお買い求めいただきたい。

発売情報： ディラック 量子力学 原書第4版 改訂版
https://blog.goo.ne.jp/ktonegaw/e/19193db48c2ca3c17c9422d1827de6d4
----------------


「ディラックにおる陽電子の予言（１９２８）」という記事で紹介した本の和訳版を２ヶ月かけて読み終えた。「ディラック 量子力学 原書第４版」だ。名著には違いないが難儀した。詳しい紹介記事を書けるほど理解できていなから、ほんの一部の内容だけ紹介することにしよう。

この本を選んだのはポール・ディラックという天才物理学者による本に触れてみたかったというミーハーな理由と、陽電子の予言という偉業がどのような形でなされたのかを発見者本人の著作によって知りたかったからだ。真空でおきている「ディラックの海」と呼ばれるエネルギー揺らぎの中から電子と陽電子が生成、消滅するという発想はどのような数式をもとに思いついたかということも知りたかった。

最初の３分の１はいわゆる「ディラックのブラ・ケット記法」の導入だ。雰囲気はまるで関数解析学の教科書のようである。波動関数を < と > という記号で略記する方法を「発明」することによって数式による表現を簡略化している。この記法の説明については次のサイトをご覧いただくとよい。

Diracのブラ・ケット記法について
http://www.ms.osakafu-u.ac.jp/~kato/braket1.html

肝心の陽電子についての理論は比較的わかりやすかった。量子力学に特殊相対性理論を加味することによって陽電子の存在を予言した。その導出のはじめの段階で中学で学習する「因数分解」が登場することを３年前の記事で紹介したが、以下がその具体的なイントロ部分である。

ニュートン力学におけるハミルトン関数は次のようになる。運動エネルギー E=(1/2)m v^2 そのものだ。



これが特殊相対性理論でハミルトン関数は次のように表現される。p0は運動量の時間成分、p1, p2, p3 は運動量の空間成分、c は光速、m は粒子の質量。速度が遅いときこの式は古典力学の場合のハミルトン関数と一致する。



この方程式によって与えられる量子力学の波動方程式は次のようになる。



しかしこの式は相対論から要求されるエネルギーと運動量の関係を与えているけれども、p0とpとの間が対称的でないから相対論的には満足のいくものではない。そこで技巧的ではあるがこの式に左側から次の演算子を掛ける。



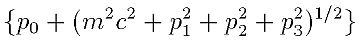
これは方程式「(a-b)=0」が与えられたときに、両辺に「(a+b)」を掛け算して「(a+b)(a-b)=0」にするようなものである。ここで「(a-b)」に対応するのが以下の数式だ。もともとの式の右辺は0なので何を掛けても0のままというのがミソである。



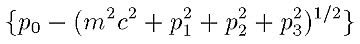
こうして、(a+b)(a-b)=a^2-b^2というおなじみの公式によって次の式が得られる。



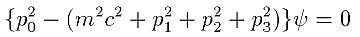
これはp0について２次式である。量子力学の一般法則から要求されるのはp0について１次式なのであるため、一見この式は奇妙である。しかしp0の値が正の場合に通常の解を与え、p0の値が負の場合に陽電子の存在を予言する数式が導かれることになる。

つまり、負のエネルギーや陽電子の発見のルーツは相対論的な時間と空間の対称性という要請によって、与えられた(a-b)=0 を a についての２次式にするために(a+b)(a-b)=0 と置いてしまうのだ。

(a-b)=0からは電子が、(a+b)=0からは陽電子が導かれる。方程式の右辺がゼロなので何を掛け算してもよいと思うと、ちょっとずるいのではという気がした。しかし実際に陽電子は実験で検出されたので問題はないのだろう。

その後の数式展開により「ディラック方程式」が導かれるのだが、その導出は以下のページを参考にするとよいだろう。相対論的量子力学の基礎方程式である。

ディラック方程式（EMANの物理学）
http://eman-physics.net/quantum/dirac.html

この記事をお読みの中学生、高校生は因数分解の利用価値がおわかりになっただろう。反物質の予言は因数分解から得られたといってもよい。１９２８年のことだ。


なお、この「ディラック 量子力学 原書第４版」は印刷が古いこともあって誤植が非常に多い。詳しくこの本を読み込んでいる方がいらっしゃるようで、以下のページで誤植訂正情報を得ることができる。この本をお持ちの方はご自身の責任において、このページの情報をもとに訂正を記入されるとよい。

メモ: 岩波書店 [ディラック 量子力學 原書第4版] の誤植及び微妙訳
http://yeblog.cocolog-nifty.com/nouse/2009/03/4-34e3.html


ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。






　　

　


「ディラック 量子力学 原書第４版」目次

I 重ね合わせの原理
量子論の必要
光子のかたより
光子の干渉
重ね合わせと不確定の性質
重ね合わせの原理の数学的な定式化
ブラ・ベクトルとケット・ベクトル

II 力学変数とオブザーバブル
１次演算子
共役の関係
固有値と固有ベクトル
オブザーバブル
オブザーバブルの関数
一般の物理的な解釈

III 表示
基礎ベクトル
δ関数
基礎ベクトルのいろいろな性質
１次演算子の表示
確率振幅
オブザーバブルの関数についての定理
記号の拡張

IV 量子条件
ポアッソンの括弧
シュレーディンガーの表示
運動量による表示
ハイゼンベルクの不確定性の原理
ずれの演算子
ユニタリー変換

V 運動方程式
シュレーディンガーの形の運動方程式
ハイゼンベルクの形の運動方程式
定常状態
自由な粒子
波束の運動
ギッブスの集合

VI やさしい応用
調和振動子
角運動量
角運動量の性質
電子のスピン
中心力の場の中の運動
水素原子のエネルギー準位
選択の規則
水素原子のゼーマン効果

VII 摂動論
一般的な注意
摂動によって生じたエネルギー準位の変化
転移の原因と考えた摂動
輻射への応用
時間に無関係な摂動による転移
異常ゼーマン効果

VIII 衝突の問題
一般の注意
散乱の係数
運動量による表示を用いた解
分散散乱
放出と吸収

IX 同じ種類の粒子をいくつか含む体系
対称な状態と反対称な状態
力学変数としての置換
運動の定数としての置換
エネルギー準位の決定
電子への応用

X 輻射の理論
ボソンの集まり
ボソンと振動子とを結びつける関係
ボソンの放出と吸収
光子への応用
光子と原子との間の相互作用のエネルギー
輻射の放出、吸収、および散乱
フェルミオンの集まり

XI 電子の相対論的な理論
１個の粒子の相対論的な取り扱い
電子に対する波動方程式
ローレンツ変換の際の不変性
１個の自由な電子の運動
スピンの存在
極座標に移ること
水素のエネルギー準位の微細構造
陽電子の理論

XII 量子電気力学
物質が存在しない場合の電磁場
量子条件の相対論的な形
シュレーディンガー力学変数
付加条件
電子および陽電子自身について
相互作用
物理的変数
理論の困難

付録 近似的な解き方
一般論
ハートリーの方法
フォックの方法
密度行列の方法


関連記事：

ディラックによる陽電子の予言（１９２８年）
https://blog.goo.ne.jp/ktonegaw/e/0764eaa33a765ffff27bccee3e35b4f3

ファインマン物理学（５）：量子力学
https://blog.goo.ne.jp/ktonegaw/e/411653135d8d38fdacb16dc0dd3f9b94

量子力学I 第２版（朝永振一郎著）
https://blog.goo.ne.jp/ktonegaw/e/7a2a6fb8e53c35ae78ee655ab68d8219

量子力学II 第２版（朝永振一郎著）
https://blog.goo.ne.jp/ktonegaw/e/05312f75b4abbb854c1a81352abebae9

角運動量とスピン（朝永振一郎著）
https://blog.goo.ne.jp/ktonegaw/e/57be844615ff28d6587522422b684221

新版スピンはめぐる（朝永振一郎著）
https://blog.goo.ne.jp/ktonegaw/e/21ec31842746c520c1bbe876616c7d77

量子力学序説（湯川秀樹著）：昭和２２年初版本
https://blog.goo.ne.jp/ktonegaw/e/bf5b874acf0b81d58d4bf8d8e66c6adf