
後日追記:この引力の計算式(↑の解析解)は間違っています。
僕は興奮している。引力を求める3重積分の解析解が求められたのだ!それも想像だにできなかった短い式でだ。僕にとってはうれしいクリスマスプレゼントになった。解析解とは数値計算ではなく文字式で表現された数式のことだ。
「物体の全質量は大きさのない質点にすべて集中しているものとして計算を行う。」というニュートン力学の大前提に疑問を持ち「質点の定理: 引力の計算式をたててみたが。。。」という記事でニュートンの公式を一般化し「大きさのある球体によって発生する引力の大きさ」を極座標で計算する3重積分の式を数式計算ソフトMaximaで解けるか試してみた。それが前回の「引力の積分式をMaximaで試す - 重心と質点の話」だった。
つまりこの3重積分の式を解析的に解こうというわけだ。

前回の記事ではいちばん内側の dr の積分を次のように求めたので、今回はその続きを行う。この途中結果までを出力するMaximaへの入力と出力結果もあわせて書いておく。(これ以降の画像は2度クリックすると拡大表示されるようにしておいた。)
integrate(((R+h-cos(t)*r)*r^2*sin(t))/(((R+h)^2+r^2-2*(R+h)*r*cos(t))^(3/2)),r);
nonzero;
nonzero;
positive;
define(f(r),%);

これに対し dr の積分区間での定積分を計算する。Maximaには出力結果を新たに関数として定義できるdefineというコマンドがあるので関数として定義しておけば、次のコマンドのために長い文字式を入力しなおす必要がない。ここでは f(r) という r の関数として不定積分を定義したわけだ。
次にこの f(r) という不定積分に積分区間を与えて引き算して得られた結果の式はθの関数なので、これをg(t)という関数に定義しておく。(Maximaで θ という文字扱えないので t で代用した。)Maximaでの入力と出力結果は次のとおりだ。
f(R)-f(0);
define(g(t),%);

このg(t)を今度は t(実際の式ではθ)で積分して不定積分を計算する。Maximaでの入力と出力結果は次のとおりとんでもなく長い式になった。こんなのが出力されていいのだろうか?出力結果の画像は4つに分割して並べておく。ことわっておくがこれ全部で1本の式なのだ。
integrate(g(t),t);




次に式で使う定数に値を入力しておく。
G: 万有引力の定数 6.67259*10^(-11)
ρ:地球の平均密度 5525(Kg/m^3): rhoという変数で代用
M: 地球の質量 5.974*10^24 (Kg)
m: 人間の質量 1 (Kg) とりあえず1Kgにしておいた。
Maximaでは次のように入力する。
G: 6.67259*10^(-11);
rho: 5525;
M: 5.974*10^24;
m: 1;
次に上記で求めたとても長い g(t) という不定積分に積分区間 -(1/2)π~+(1/2)πを代入して定積分を計算する。そしてその左にいちばん外側の dφ についての定積分の結果=2πを掛け、最初の3重積分の積分記号に前置きされるm, ρ, Gなどの定数を掛ける。これですべての計算が終わり、3重積分はRとhの2変数関数としてF=の右側が解析解として求められるはずだ。
理屈の上ではそうなのだが上のように複雑な関数g(t)に対してMaximaはちゃんと計算してくれるだろうか?以下がMaximaへの入力と出力結果だ。
rho*m*G*2*%pi*(g(%pi/2)-g(-%pi/2));

えっ!たったこれだけ??
僕は驚いた。上の4つの画像で示した巨大な式がまるで結晶が固まるように、こんなに小さな式にまとめられたのだ。すごい!僕にはまるで神様の手がとても難解なパズルを一瞬で解いたように見えた。出力されるまでほんの1秒ほどだった。積分区間の上限値と下限値の-(1/2)πや(1/2)πが t に代入されることで式の中の cos(t) がすべてゼロになるから式全体が短くなるのはわかるが、それにしても短くなりすぎなのだ。
でもこの結果は合っているのだろうか?Maximaが間違えるということはあるのだろうか?Mathematica使っている人に同じことやって検算してもらいたいところだ。
とりあえずこの式をTeXを使って整形するとこのような式になった。

絶対に解けないと思っていた積分は解けたのだ。ことわっておくがこれが以下の3重積分の解析解である。(積分定数Cは省略)

そしてその意味は、地球を構成する微小体積要素のそれぞれが万有引力の法則にしたがって人間を引っ張っているときに、その総合計の引力を計算するものだ。Rとhの意味はこの図のとおりである。
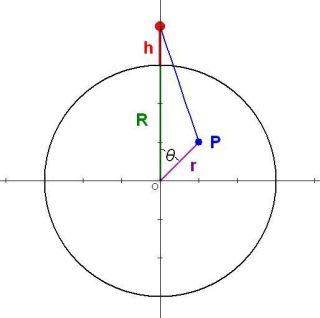
積分は次のような極座標を使うのだ。
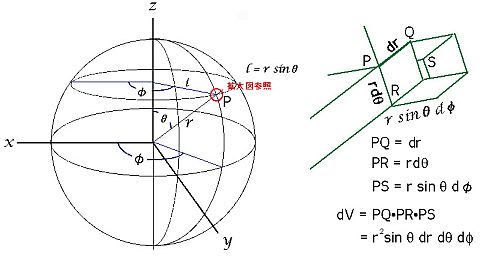
そして積分計算で得られた引力の式と、地球を大きさのない質点とおいたオリジナルの万有引力の公式を上記の図にあてはめた以下の式と比較してみようというのが目的なのだ。
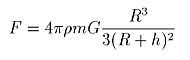
くどいようだが比較する式はこれである。(クリックすると拡大表示する。)上の式を大きさのある現実の地球にあてはめた、いわば一般解、修正解とも言うべき式である。

解析解は求められたが、もしかしたらMaximaは間違えているかもしれないので検証が必要だ。とりあえず以下の2つの方法でこの式の検証してみることにする予定だ。
1)上記の2つの式に具体的な数値を代入して値の違いを比較する。
2)3重積分で表現された引力の式に対してパソコンを使った数値積分の計算を行って、解析解から得られる数値解と比較を行う。
楽しみにしていただきたい。
-------------------
翌日に追記:

ここに至って僕は単純で重大なミスをおかしていることに気がついてしまった。計算をはじめるにあたって設定した3重積分の中に誤りを見つけたのだ。でも、ご安心を!はじめから計算をやりなおせばいいのだから。僕が設定した積分式だと地球の北半球部分だけの引力しか計算できていないのだ。それも北半球2個ぶんで重複して求めてしまっている。積分区間は北半球と南半球で別々に設定しなければならなかったのだ。
このミスはこのページで得られた解析解の検証をはじめた過程で数値が合わなかったので、どうしてだろうと考えているうちに気がついたのだ。でもミスのおかげでとても興味深い事実を発見することになった。また、北半球と南半球を別々に解く正しい計算方法でもちゃんと解析解が得られるであろうことも確信できた。神様が難解なパズルを解いたのは幻ではなかった。ミスから得られた「棚からぼた餅」についても楽しみにしていただきたい。
この話は次の記事に続く。
12月28日に追記:
ニュートンの質点の定理はその後、この記事にコメントをいただいている☆さんという方から教えていただいた。その証明はこちらの記事や以下のコメント欄からご覧いただきたい。
また「ファインマン物理学(1)」の191ページにも、この定理の証明が掲載されていたのを後になって気がついた。このページにその証明を掲載しておく。
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。



関連記事:
万有引力についてのこの一連の記事を最初から読みたい方は、「僕が物理や数学にハマりだしたきっかけ - 重心と質点の話」という記事からお読みください。
僕は興奮している。引力を求める3重積分の解析解が求められたのだ!それも想像だにできなかった短い式でだ。僕にとってはうれしいクリスマスプレゼントになった。解析解とは数値計算ではなく文字式で表現された数式のことだ。
「物体の全質量は大きさのない質点にすべて集中しているものとして計算を行う。」というニュートン力学の大前提に疑問を持ち「質点の定理: 引力の計算式をたててみたが。。。」という記事でニュートンの公式を一般化し「大きさのある球体によって発生する引力の大きさ」を極座標で計算する3重積分の式を数式計算ソフトMaximaで解けるか試してみた。それが前回の「引力の積分式をMaximaで試す - 重心と質点の話」だった。
つまりこの3重積分の式を解析的に解こうというわけだ。

前回の記事ではいちばん内側の dr の積分を次のように求めたので、今回はその続きを行う。この途中結果までを出力するMaximaへの入力と出力結果もあわせて書いておく。(これ以降の画像は2度クリックすると拡大表示されるようにしておいた。)
integrate(((R+h-cos(t)*r)*r^2*sin(t))/(((R+h)^2+r^2-2*(R+h)*r*cos(t))^(3/2)),r);
nonzero;
nonzero;
positive;
define(f(r),%);

これに対し dr の積分区間での定積分を計算する。Maximaには出力結果を新たに関数として定義できるdefineというコマンドがあるので関数として定義しておけば、次のコマンドのために長い文字式を入力しなおす必要がない。ここでは f(r) という r の関数として不定積分を定義したわけだ。
次にこの f(r) という不定積分に積分区間を与えて引き算して得られた結果の式はθの関数なので、これをg(t)という関数に定義しておく。(Maximaで θ という文字扱えないので t で代用した。)Maximaでの入力と出力結果は次のとおりだ。
f(R)-f(0);
define(g(t),%);

このg(t)を今度は t(実際の式ではθ)で積分して不定積分を計算する。Maximaでの入力と出力結果は次のとおりとんでもなく長い式になった。こんなのが出力されていいのだろうか?出力結果の画像は4つに分割して並べておく。ことわっておくがこれ全部で1本の式なのだ。
integrate(g(t),t);




次に式で使う定数に値を入力しておく。
G: 万有引力の定数 6.67259*10^(-11)
ρ:地球の平均密度 5525(Kg/m^3): rhoという変数で代用
M: 地球の質量 5.974*10^24 (Kg)
m: 人間の質量 1 (Kg) とりあえず1Kgにしておいた。
Maximaでは次のように入力する。
G: 6.67259*10^(-11);
rho: 5525;
M: 5.974*10^24;
m: 1;
次に上記で求めたとても長い g(t) という不定積分に積分区間 -(1/2)π~+(1/2)πを代入して定積分を計算する。そしてその左にいちばん外側の dφ についての定積分の結果=2πを掛け、最初の3重積分の積分記号に前置きされるm, ρ, Gなどの定数を掛ける。これですべての計算が終わり、3重積分はRとhの2変数関数としてF=の右側が解析解として求められるはずだ。
理屈の上ではそうなのだが上のように複雑な関数g(t)に対してMaximaはちゃんと計算してくれるだろうか?以下がMaximaへの入力と出力結果だ。
rho*m*G*2*%pi*(g(%pi/2)-g(-%pi/2));

えっ!たったこれだけ??
僕は驚いた。上の4つの画像で示した巨大な式がまるで結晶が固まるように、こんなに小さな式にまとめられたのだ。すごい!僕にはまるで神様の手がとても難解なパズルを一瞬で解いたように見えた。出力されるまでほんの1秒ほどだった。積分区間の上限値と下限値の-(1/2)πや(1/2)πが t に代入されることで式の中の cos(t) がすべてゼロになるから式全体が短くなるのはわかるが、それにしても短くなりすぎなのだ。
でもこの結果は合っているのだろうか?Maximaが間違えるということはあるのだろうか?Mathematica使っている人に同じことやって検算してもらいたいところだ。
とりあえずこの式をTeXを使って整形するとこのような式になった。

絶対に解けないと思っていた積分は解けたのだ。ことわっておくがこれが以下の3重積分の解析解である。(積分定数Cは省略)

そしてその意味は、地球を構成する微小体積要素のそれぞれが万有引力の法則にしたがって人間を引っ張っているときに、その総合計の引力を計算するものだ。Rとhの意味はこの図のとおりである。

積分は次のような極座標を使うのだ。

そして積分計算で得られた引力の式と、地球を大きさのない質点とおいたオリジナルの万有引力の公式を上記の図にあてはめた以下の式と比較してみようというのが目的なのだ。
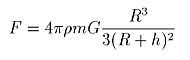
くどいようだが比較する式はこれである。(クリックすると拡大表示する。)上の式を大きさのある現実の地球にあてはめた、いわば一般解、修正解とも言うべき式である。

解析解は求められたが、もしかしたらMaximaは間違えているかもしれないので検証が必要だ。とりあえず以下の2つの方法でこの式の検証してみることにする予定だ。
1)上記の2つの式に具体的な数値を代入して値の違いを比較する。
2)3重積分で表現された引力の式に対してパソコンを使った数値積分の計算を行って、解析解から得られる数値解と比較を行う。
楽しみにしていただきたい。
-------------------
翌日に追記:

ここに至って僕は単純で重大なミスをおかしていることに気がついてしまった。計算をはじめるにあたって設定した3重積分の中に誤りを見つけたのだ。でも、ご安心を!はじめから計算をやりなおせばいいのだから。僕が設定した積分式だと地球の北半球部分だけの引力しか計算できていないのだ。それも北半球2個ぶんで重複して求めてしまっている。積分区間は北半球と南半球で別々に設定しなければならなかったのだ。
このミスはこのページで得られた解析解の検証をはじめた過程で数値が合わなかったので、どうしてだろうと考えているうちに気がついたのだ。でもミスのおかげでとても興味深い事実を発見することになった。また、北半球と南半球を別々に解く正しい計算方法でもちゃんと解析解が得られるであろうことも確信できた。神様が難解なパズルを解いたのは幻ではなかった。ミスから得られた「棚からぼた餅」についても楽しみにしていただきたい。
この話は次の記事に続く。
12月28日に追記:
ニュートンの質点の定理はその後、この記事にコメントをいただいている☆さんという方から教えていただいた。その証明はこちらの記事や以下のコメント欄からご覧いただきたい。
また「ファインマン物理学(1)」の191ページにも、この定理の証明が掲載されていたのを後になって気がついた。このページにその証明を掲載しておく。
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。
関連記事:
万有引力についてのこの一連の記事を最初から読みたい方は、「僕が物理や数学にハマりだしたきっかけ - 重心と質点の話」という記事からお読みください。
























また、物理学の基礎的な問題はもう立派に研究し尽くされ、教科書を見れば全て載っている気がしたんですが、今回のとねさんの重心と質点のはなしは初めて知りましたし、意外とまだまだ一個人としても様々な考察をし、深めることが出来るのだなと感じました。
うちの学校のPCにMATHEMATIACA入ってるんで冬休み明けにいじってみようかな・・・
南半球を考慮にいれた再計算はきっとうまく行く気がします。楽しみにしてます!!!
Merry Christmas :)
こんにちは。1週間スキー合宿と書いてありましたので、戻ってこられるまでにある程度の結果をお見せできればいいなと思っていましたが、合宿している場所にネット環境があったわけですか。(笑)
再計算がんばりますよ。
ミネルヴァさんはMathematicaを使える環境にいらっしゃるのですね!うらやましいです!僕の再計算の結果が掲載されたら、ぜひ同じことをMathematicaでも試してみてください。(現状の結果を試してもいいですけど。)
結果は,ニュートン力学の大前提で計算した結果と同一になりました.
こんなふうに確かめるのも面白いですね!
お久しぶりです!Maximaで計算できたのですか!
それはすごいです。
ぜひやり方を教えてください。どこかのページに作成して、ここのコメント欄にリンクを張っていただけると助かります。
実はこれって、次の記事にも書いたように、僕は物理現象の検証を超えた重大な意味があると思うのですよ。320年もの間「決め事」であった定理が「証明」に変わるわけですから。もちろんMaximaを使った解析解を使うというのが証明の根拠として許されるならばですけれども。
今日やったら何かおかしな結果になりましたので,
積分をするサイトを使って計算してみました.
結果をまとめたページを以下に用意しました.
http://www14.ocn.ne.jp/~euler/newtoncalc.htm
やはりニュートンの前提で計算した結果と一致するようです.
ありがとうございます!
すごい!合ってますね!!☆さんのページの解法を何度も読み直してみましたが、証明できていると思います。積分の結果が見事にニュートンの結果に一致しています!僕の立てた式は積分区間が間違っていましたね。(積分順序が違うのは本質的な違いじゃないですけど。)
この計算手順ってこれまで誰かがどこかに発表していましたっけ?そうでないと、ニュートンの定理は僕が知っている限り「決め事」であったと思うので。
やっぱり、これは快挙ではないでしょうか?「地球を8000万個に分割してみた」のほうの記事で「のぶゆきさん」という方が「ノーベル賞ものですよ。」のようなコメントをされています。
この問題の証明って、過去に誰かが発表されたことがあるのかご存知ですか?
また、☆さんの証明のページの内容を「☆さんという方が証明されたのですけど。」という感じにして、本編の記事として書いてもよろしいでしょうか?
なんだかドキドキしてきました。
大きさのある物体へのニュートンの万有引力の適用は,いろいろな
ところに載っているようです.ニュートン自身も,当てずっぽうに
球の中心を質点と見なしたのではなく,他の物理学者に文句を
つけられないようにキチンと計算した上で,「球の中心に質点があると
置き換えてもいい」としたのではないかと思います.
ニュートン自身はそこまで深く考えなかったかもしれませんが…
今回の計算はどうぞ記事にしてください.難しい式の証明も
数式処理ソフトを簡単に出来て面白いですね!
証明は既に誰かが発表していたのですね。がっかりというより、ほっと安心しました。(笑)
この積分は確かに難易度は高いですが、フェルマーの定理や、ポアンカレ問題に比べれば、「小学生レベル」ですし、きっと誰かが証明してるに違いないとは感じていました。
それでも、この質点定理がいまだに証明されたことだというのは僕は見かけたことがないのが不思議でした。力学の教科書に書いておけばよいのにと思います。力学の根幹の問題なのですから。(と☆さんに愚痴っても仕方ありませんね。(笑))
Mathematicaでの積分はWebサイトでできるんでしたね。(僕は忘れていました。) どうもMaxima不審に陥ってしまいそうです。もう☆さんがMathematicaに入力した式をMaximaで試してみますね。
☆さんの証明を記事にする件を承諾いただき、とてもうれしく思っています。ただ証明するだけでなく、僕の文章を付して「読み応えのある」面白い記事を書きたいと思っています。
あと、重心と質点についての記事は、ネタを3つほど頭の中であたためています。☆さんにとっては既にご存知か、昔同じことを考えていらっしゃったかもしれませんが、記事を掲載しましたらどうかまたお読みになってください。
ありがとうございました!