引力の積分式をMaximaで試す - 重心と質点の話

「僕が物理や数学にハマりだしたきっかけ - 重心と質点の話」という記事からはじまった万有引力の記事について「質点の定理： 引力の計算式をたててみたが。。。」という記事で紹介した引力の大きさを極座標で計算する３重積分の式を数式計算ソフトMaximaで解けるか試してみた。いちばん外側の dφ の積分は変数φが積分内部の式に登場しないので２πが乗数として外にでる。だから実質的には dr と dθ の２重積分だ。

まず、いちばん内側のdrでの不定積分をMaxima行う。この部分だ。


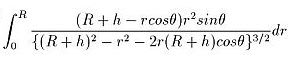
次のコマンド実行する。θはMaximaに入力できないので t で置き換えて入力した。

integrate(((R+h-cos(t)*r)*r^2*sin(t))/(((R+h)^2+r^2-2*(R+h)*r*cos(t))^(3/2)),r);

以下はMaximaからの出力結果だ。画像を続けて２度クリックすると拡大表示される。



出力結果をTeX形式にしてきれいな数式に整えるとこのようになった。こういうのを解けるなんて確かににMaximaはすごい。でも、これじゃ後が続かない。。。物理学の数式には現実世界の意味との関連があることが多いのだが、こんなに複雑だと意味を読み取ることは不可能だ。

この画像も続けて２度クリックすると拡大表示される。


ここで僕はくじけてしまった。やはり数値計算しかないかな。
いや待てよ。積分は計算できているのだからあきらめるのはまだ早い。もう少しねばってみることにしよう。

この話は次の記事に続く。

ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。