行列の固有値で表される離散的、選択的な自然現象

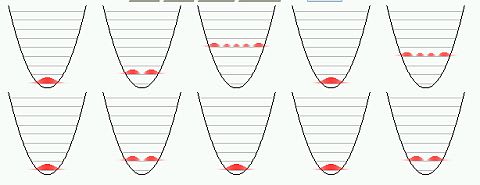
掲載画像は小田垣孝先生のサイトに掲載されている統計力学のJavaアプレットのスクリーンショットなのだが、これは量子力学的にエネルギーの遷移する様子を表現すると調和振動子の現象として説明されることを示している。（アプレットはこちら。）

つまりエネルギーとは連続的に変化するのではなく、このようにとびとびの値をとりながら変化しているわけで、「E = hν」の式であらわされるようにエネルギーが粒子として存在していることがわかり、これが量子力学のスタート地点となった。

エネルギーが変化する様子：


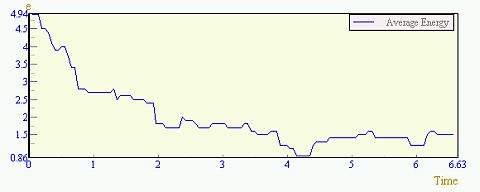
とびとびの値をとりながら変化するエネルギーの値は、量子力学では行列の固有値として求められている。ミクロなレベルでの量子の状態は複素数の波動関数であらわされ、その振動が上記アプレットで見られるような「調和振動」なのだ。（量子力学的な解説はこのページをお読みいただける。）

高校の数学で習う行列の固有値や固有ベクトルは大学レベルの物理学ではこんな不思議な現象の説明に使われることになる。１次変換の拡大方向、拡大率という意味はその導入にすぎない。



多くの粒子がつながった状態で振動している場合、そこにはいくつかの振動パターンが観測される。古典力学系ではこのようにバネにつなげられた３つの球の運動も、力学的な運動方程式（微分方程式）をたてると、それが行列の固有値の問題として解けることがわかる。（この問題と解法はこちら。３９ページあたりからお読みいただきたい。）



このような３つの球の連成振動は３ｘ３の行列の方程式であらわされるから固有値も固有ベクトルも３つずつ求められる。振動パターンが３種類なのも固有値の数で説明がつく。

一般化するとＮ個の球であればＮｘＮの行列の方程式になるわけで、固有値を解として導く固有値方程式はＮ次のべき関数方程式で求められるから固有値の数はＮ個となり、振動パターンもＮ種類となるわけだ。球の数が多いと振動パターンがとても多くなりそうな気がするものだがＮ種類に限定されることがわかるのは不思議な気がする。

このような振動パターンは「固有振動」と呼ばれている。地球も大きな弾性体であり非常に長い周期で振動していることは地球物理学者の竹内均先生によって計算された。（竹内先生はいちばん長周期である５４分の地球自由振動を計算で求めた。）



これが現在知られている地球自由振動のパターンで振動周期は左から54分、26分、12分、4分である。これらも微分方程式から得られる行列の固有値問題の応用だ。

関数をよりどころとして速度や加速度、方向など連続した物理量でとらえる古典的な物理学は一気に、「とびとびな値をとる物理量」や「いくつかのパターンに分類される物理現象」など離散的、選択的な物理現象を説明する近代的な物理学へ発展した。

振動パターンが違うと人はその系全体の現象を違ったものとして判断することがある。バイオリンの音色とピアノの音色の違いは音波の振動パターンの違いだ。それらを人間の耳が区別している理由も同じような行列の固有値に見出すことができそうである。


ブログ執筆のはげみになりますので、１つずつ応援クリックをお願いします。