前回の問題は、1次関数 Y=aX+2 の a を求める問題でした。
a を求めるために 図形を利用しました。
図解は、よく見ますと長方形と台形です。
長方形と台形の頂点の座標が分かれば面積が分かるはず!
というわけで、解答は
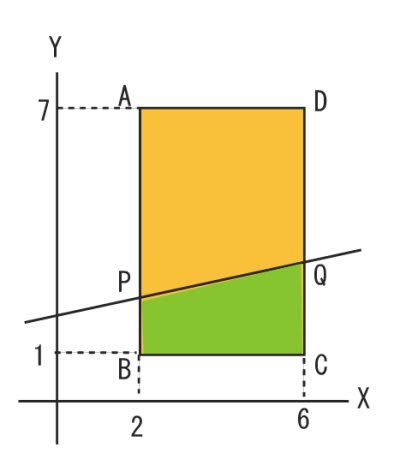
直線Y=aX+2 と 辺AB、DCとの交点をP、Qとしますと
下の台形の面積は (上底+下底)×高さ÷2 ですから
(PB+QC)×BC÷2で、これが長方形ABCDの3分の1になります。
PBはPのY座標(2a+2)から BのY座標1を引いた数で 2a+1
QCはQのY座標(6a+2)から CのY座標1を引いた数で 6a+1
高さは、BCの長さで 4
長方形ABCDの面積は 縦6 横4 で、24
これを式にしますと
((2a+1)+(6a+1))×4÷2=24÷3 となり
これを解いて a=1/4 (または、0.25)
座標の中に図形が出てきたときには、
各頂点の座標を考えましょう。また、底辺が下にくるとは限りません
問題用紙をグルグルまわしてみると分かりやすい位置が見えてくるかも・・・













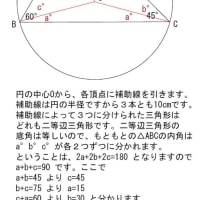
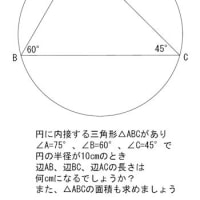
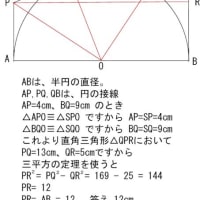
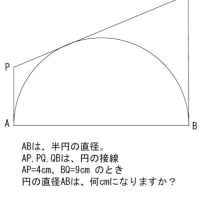
※コメント投稿者のブログIDはブログ作成者のみに通知されます