1次関数の応用！代表問題～

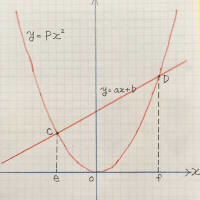
この図は、よく出てきますね～

さて、前回の問題。

三角形△ABPの面積が１２８㎠になるとき

点Pは、Bを出てから何秒後か？という問いでした。

Pは秒速１ｃｍでしたから 経過時間と移動距離の数字は同じになります。

これは、簡単かな？Pの移動距離（移動時間と同じ）をX としますと

底辺×高さ÷２＝１２８  ですね

AP×BP÷２＝１２８

１６×（X）÷２＝１２８  より

（X）＝１６  となります。

が！

これだけではない。もう１つありますね。

P がDからAに向かうときに、AP＝１６の時も

同じ面積になります。そのときの（X）は、

（X）＝BC＋CD＋DP＝２０＋１６＋（２０－１６）＝４０

よって答えは、１６秒後と４０秒後

 

もう一つの問題

P が DからAに向かうときの△ABPの面積 Y を表す式は

Y＝１６×AP÷２

Y＝１６×（BC＋CD＋DA－X）÷２

Y＝１６×（２０＋１６＋２０－X）÷２

これを整理します

Y＝－８X＋４４８

 

 

これも一度経験すれば、仕組みはさほど難しいものではないと思います。

初めての場合はできなくても、2回目からは計算できるでしょう～

この問題専用の公式は、ありませんから  仕組みを理解しましょう