1次関数と 座標 の 親密な関係～

前回、最後の問題を

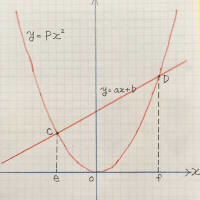
方眼紙に描いてみますと  このようになります。

３つの１次関数の交点を P、Q、R としますと

この３つの関数で囲まれた図形は△PQRです。

関数AとBの交点 Pを通って この三角形を２等分する線は

QとRの中点 S を通ります。

２点 SとPを通る関数の式は

SからPに 移動するときに Xは３増加して  Yは４増加しますので

変化の割合（傾き）は、３分の４！

Y=４／３X＋ｂ  の式に、点P（または点S）の座標（X=２、Y=２）を代入しますと

ｂ＝－２／３  （マイナス３分の２）となり

求める関数の式は  Y=４／３X－２／３ 

 

この問題のように方眼紙に描いて、

交点がはっきり分かるような式だと簡単ですが

方眼紙でははっきり分からない場合は、計算で求めます。

２つの関数の交点は、２つの関数の連立方程式の答えと同じ。

（交点のＸとＹの値は、どちらの関数でも有効です）

また、方眼紙に描いてみてはっきり分かることは

Ｙ＝２Ｘ＋１  と

Ｙ＝２Ｘ－１  の  連立方程式には  答えがありません。

この２つの関数は、平行になっていて交差しませんから。