
前回の問題は、この赤い印のついた角の合計は何度?
という問題でした。
さてさて、これは何角形になるのか?って考えると
なかなか答えにたどり着きません~
そこで利用するのが、一番内側にある9角形!

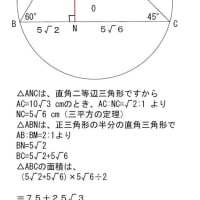
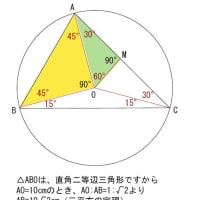
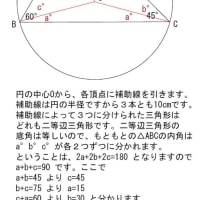
赤と水色と黄色の印がついた三角形が9個ありますね
ここで、水色の印のついた角は、内側の9角形の外角です。
水色の印のついた外角は全部で9つあり、その合計は360°
まあ、もともと外角の合計は何角形であっても360°になりましたよね、
覚えてますか?
同じように黄色の印のついた角の合計も360°
赤と水色と黄色の印がついた三角形は9個ありましたから
その9個分の内角の和から水色の印のついた角の合計360°と
黄色の印のついた角の合計360°を引けば、
残るのは 赤い印のついた角の合計です。
式は
180×9-360-360=900 答え900°
別の考え方:
最初に円周を9等分しても答えは同じになるはずですから
円周を9等分し、そのうちの5つぶんの円周角を計算してもOKです。
3年生になったら円周角を習います。













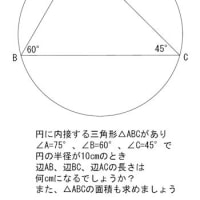
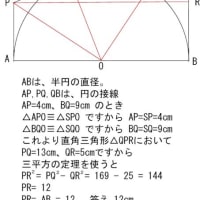
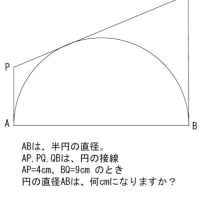
※コメント投稿者のブログIDはブログ作成者のみに通知されます