光速で移動しながら鏡を見たら

今回は光の等価原理で、

そのはじまりはアインシュタインが16歳のときに抱（いだ）いた次の疑問でした。「もし自分が光の速さで飛んだら、顔は鏡（かがみ）に映るのだろうか？」顔が鏡に映るには、顔から出た光が鏡に達し、反射して自分の眼にもどってくる必要があります。しかし自分が光と同じ速さで動いていたらどうでしょう？　光は前には進めず、鏡に届かないのではないでしょうか？　しかしアインシュタインは「止まった光」などありえないのではないかと考え、悩みました。【『みるみる理解できる相対性理論　改訂版』ニュートン別冊／佐藤勝彦監修、水谷仁編集（ニュートン　プレス、2008年）以下同】

という思考実験を「光速度基準＋ニュートン力学」で考えてみましょう。

お互い様に時間が遅れる光速度不変の原理や、進行方向にだけ収縮するローレンツ変換は、全く無用で複雑にするだけなので、さっさと仮定から取り除きましょう。

^ ガリレイ変換自身は、絶対静止座標系の概念とは無関係である。

したがって、自分を加速する場合は速度無制限です。
いくらでも自分の時間を遅らせて、加速できます。
だから運動する内部の生活は、光速度のままなので鏡に写ります。

ニュートン力学では、宇宙における絶対静止座標系が存在しないので、あらゆる速度は常にその時々の観測者から見た相対速度である。 

自分の時間(観測者からみた時間を光速度基準にします。)は、光速度ｃで流れるのは変わりません。

外の光速(We²)＝中の光速(Wi²＝c²)＋中から見た後退速度(Vi²)

Vi=0の時は、We=Wiで時間の流れは同じですが、
Vi>0の時は、We＞Wiは超光速になり、その比Wi/Weが時間の遅れです。

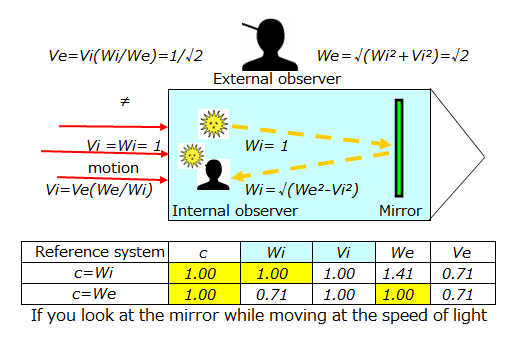
たとえば、光速度の1倍の後退速度Vi=Wiで移動すると、元の光速We＝√(１＋1)、Wi/We＝1/√２に時間が遅れます。

それは外部観測者から見た前進速度Ve＝Vi(Wi/We)＝1/√2倍です。

一般に加速すると自分の時間が遅れるといいますが、逆に自分の時間を遅らせることは、加速することとも言えます。