Abstract
観測者は地球の自転によって等方的に収縮し、そして超光速の光伝搬(フライバイ・アノマリー)を体験する。
前に、Draftで「Frequency shift and Flyby anomalies 」を書いたんだけど、ちゃんと説明しておこうと思う。
フライバイ異常現在の科学的モデルと速度の実際の増加(すなわちにおける増加との間の不一致である運動エネルギーの間に観察された)遊星フライバイ宇宙船によって(通常は地球の)。複数のケースで、宇宙船は科学者が予測したよりも速い速度を得ることが観察されていますが、これまでのところ説得力のある説明は見つかりませんでした。この異常は、SバンドおよびXバンドの ドップラーと測距テレメトリのシフトとして観察されています。フライバイ中に気づいた最大の不一致は13 mm / sです。[1]
フライバイ異常については、次のようないくつかの説明が提案されています。
- フライバイ異常は、光の速度がすべてのフレームで等方性であり、ドップラー効果によって宇宙探査機の速度を測定するために使用される方法で不変であるという仮定の結果であると仮定されています。[14]測定された一貫性のない異常値:正、ヌル、または負は、この仮定を緩和して簡単に説明されます。フライバイ操作中、観測者の方向のプローブの速度成分Voは、プローブによって送信された無線周波数fの相対変位dfに、ドップラー効果によって光のローカル速度c 'を掛けたものから導出されます。Vo =( df / f)c '。セスペデス・キュレ仮説によれば、[15]可変重力エネルギー密度場を通過する動きにより、空間の屈折率n 'がわずかに変化するため、光の速度c'がわずかに変化し、不変量cに基づくドップラーデータの補正が行われます。これにより、地球の基準座標系でのフライバイ操作の速度またはエネルギーの変化が誤って推定されます。
- 考慮されていない横方向ドップラー効果—つまり、放射状速度がゼロで接線速度がゼロでない光源の赤方偏移。[13]ただし、これは、レンジングデータの同様の異常を説明することはできません。
光の非対称ドップラー効果による説明。
運動する物体や観測者は等方向に収縮(光速も、物体の長さも、時計の進み方も同期して変化するので、同じ慣性系の光速は一定)するので、回転でなくても運動する観測者を基準にすると相対的に全方向の光速が速くなる。
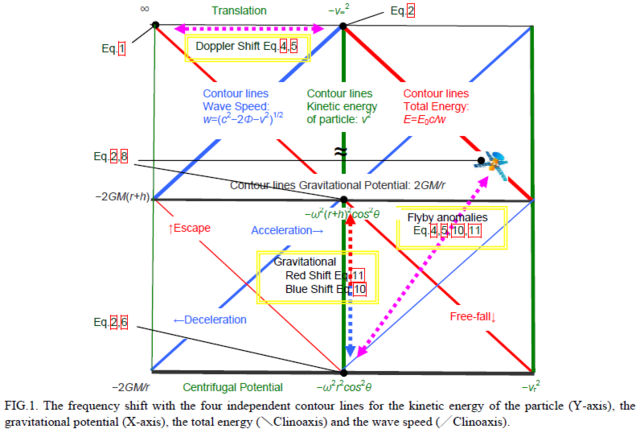
DSNの観測者は自転運動( ω R cos θ )により等方向に収縮しているので、その観測者を光速度( C )の基準にすると、上の図の左(自転軸や双曲線無限遠)からの光速( W₊ )は相対的に超光速になる。
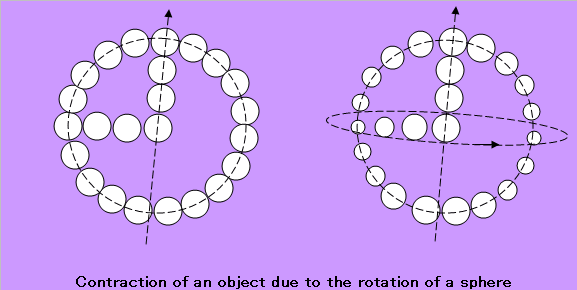
W₊=√(C²+[ω R cos θ]²) (1)。
DSNの観測者の収縮による光速の差(C<W₊)は、探査機の無限遠速度の差(V∞'<V∞)に現れる。
V∞=(W₊/C)V∞'、
√(V∞²-V∞'²)/V∞≅ω R cos θ/C (2)。
この観測者が運動する場合、光の非対称ドップラー効果の観測周波数(f)は、
f=f₊/(1-V₊ cos α/W₊) (3)。
α:観察者から見た光源の移動角度=光源の移動方向からみた観測者の角度。
運動する観測者から発し対象から反射する往復信号に、その運動分の二次ドップラーシフト(f₊)は現われない(参考:以下の図の(d))。

しかし、プライマリー・ドップラーシフトにフライバイ・アノマリーは現れる。
⊿f/f₀=(f-f₀)/f₀=⊿V∞ cos α/W₊ (4)。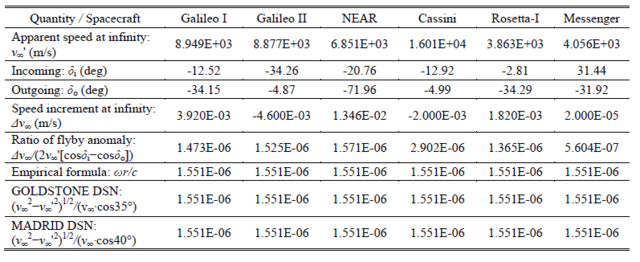
(式4)のα(偏角δi とδo の2方向は地球の赤道を基準)と、(式2)の緯度θにあるDSN局と結び付けると、以下のアンダーソンの関係式になる。
⊿V∞/(2 V∞’[cos δi-cos δo])=ω R/C=√(V∞²-V∞'²)/(V∞ cos θ) (6).
結論
Mbelekは「本アノマリーは特殊相対論における横ドップラー効果のみかけである。」と述べているが、非相対論的なプライマリー・ドップラー式へキャストして説明している。これは光速度に合わせて時間が遅れ、進行方向に時空が収縮しただけでは現象を説明できないことを意味していて、
ローレンツ:絶対時間+進行方向に物体が収縮、
アインシュタイン:相対時間+進行方向に時空が収縮、
本論:相対時間+等方向に物体が収縮。
時間が遅れ、物体が等方向に収縮し、運動する観測者の系に相対して他の系の光速が速くなり、距離が増した結果、ドップラー効果やレンジングデータにフライバイ・アノマリーが現れる。したがって光の非対称なドップラー効果の式が変わってくる。
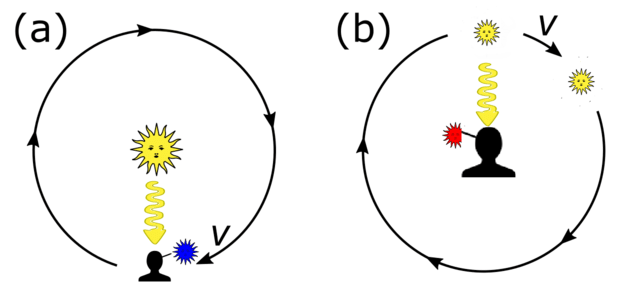
この結果は、光速度の観測基準系が運動により等方向に収縮したことが観測されたことになるので、以下の見直しが必要になる。
フライバイ・アノマリーのように、近傍で我々の時間の進み方より早い現象の大きな差異を得るのは難しく、長らく光速度不変に頼ってきたが、古典力学から光速度基準へのパラダイムシフトが、まだまだ中途半端ともいえる。
謝辞
このフライバイ・アノマリーの提唱のリーダーであったアンダーソン博士がメールへの返事やサイトのフォロワーになってくれたのと、Webで議論してくれた人々に感謝する。










※コメント投稿者のブログIDはブログ作成者のみに通知されます