[2023年3月22日 更新]
入試は過去問題をきっちり分析している者が有利に決まっている。
都立高校入試も例外ではなく傾向がある。それを解説する。
◆相似と合同 出る割合は50:50
都立入試の数学では必ず大問4で平面図形の証明問題が出る。
得点は毎年7点。途中点もあり。
「難しそう」でハナからあきらめる受験生もいるが、これは絶対にトライすべき問題。
まずは過去の傾向を見てみよう。
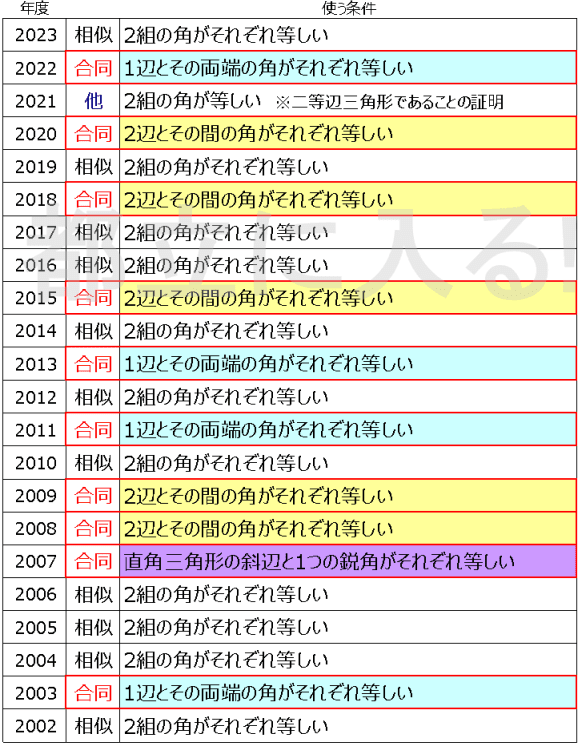
相似条件は「2組の角がそれぞれ等しい」しか出ない。
よって相似の証明だったらラッキーと思おう。2組の等しい角を見つけるだけだ。
合同条件も「2辺とその間の角がそれぞれ等しい」か「1辺とその両端の角がそれぞれ等しい」のどちらかだ。
一度、直角三角形の合同条件はあったが、10年以上出ていない。
そして断言する。
「3辺がそれぞれ等しい」という合同条件は絶対に出ない。
問題が作りにくいからだ。
証明問題の出る順番にもヒントがある
証明問題は、大問4の1問目か2問目に出る。
どっちで出るかで問題の難度が分かる。
当然、1問目に出たほうが解きやすい問題だということになる。
1問目だったら、チャンスと思ってほしい。
とは言え、ここ17年間は2問目に出ている。おそらく2024年度も同じだ。
◆2024年入試 何が出るか
私は「合同の証明」とにらんでいる。
傾向を見ると、1年おきに相似・合同・相似・合同・・・というケースが多い。
大きな声で言えないのだが、
後期募集・2次募集の入試が相似なら、翌年の一般入試も相似
後期募集・2次募集の入試が合同なら、翌年の一般入試も合同
という傾向がある。
2023年度の後期募集・2次試験は合同の証明だった。
ということで、おそらく2024年度の都立入試では「合同の証明」だ。
都立に入る! ツイッター 毎日の更新情報を受け取れます














コメントを投稿するにはgooブログのログインが必要です。