勤務先の夏休みの初日に息子と数学の勉強。
息子が通っている予備校の夏期講習テキストに、またまた受験生が困りそうな問題がありました。
ちっと、文系のレベルを超えていると思い、回答を作ってみました。
S台予備校のテキストでは、「論証」というくくりでまとめられている問題です。
要は、平面上で(x,y)の領域が与えられ、その(x,y)の取り得る条件下で、「x+y」の最大値を求めなさい、、、
という問題です。

たいがい、(x,y)の取り得る「領域」は、受験生にも容易に図示できます。
例えば、「x+y」の最大値を問われれば、
x+y=k
と置き、これを
y=-x+k
と変形し、y切片が「k」で、傾きが「マイナス1」の直線(一次関数)と考え、
平面上に描いた「領域」を、直線が通過するときの最も小さなy切片を求めれば、これが「x+yの最小値」となります。
ところが、このK大の問題で与えられた「領域」は、
x^2 -2xy +2y^2 = 4 ・・・①
で、「-2xy」が邪魔になって、見慣れた楕円の式
(x/a)^2 + (y/b)^2 = 1
に変形できず、「領域」を図示できません。
実は、「xy」項が入ると、下図のように楕円が回転します。
なお、回転した楕円の作図が課題でないため、下図の楕円の傾きは正確なものではありません。
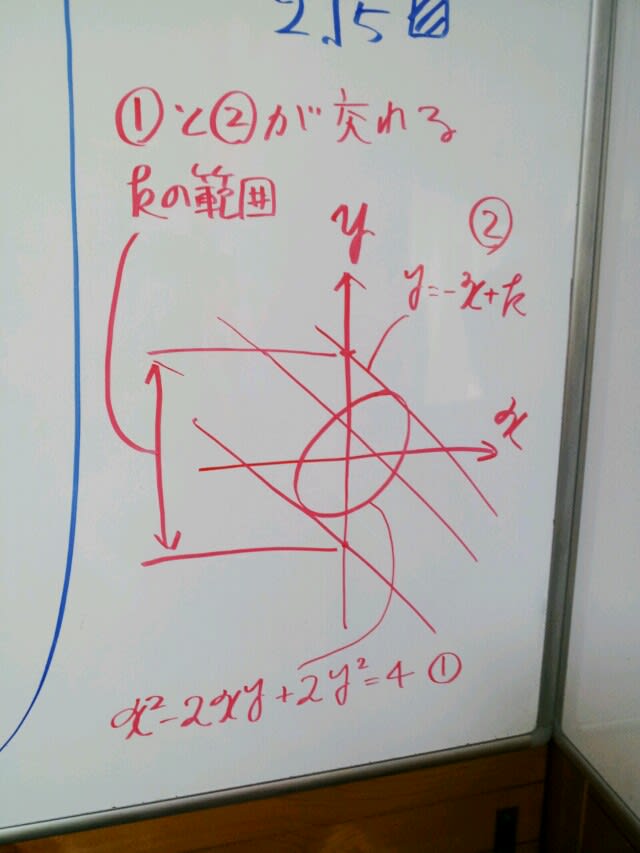
この楕円の作図は、理系でもなかなか出来ないので、どう解こう(汗)、、、となります。
結論は、やり慣れた図形的な検討からの解答ではなく、
x^2 -2xy +2y^2 = 4 ・・・①
に
y=-x+k
を代入して、xの二次方程式(係数にkの式を持つ)とし、判別式をたてます。
判別式≧0
とすると、kの範囲が得られます。
このkの範囲の上限が、「x+y」の最大値となります。めでたし
因に、下が自分用の自宅数学教室用セットです。

パイロットのボードマスターの、「書き味」と「消し味」が気に入り、
ネット通販で、替芯と替えインクをまとめ買いしました。
あと、一本だけ横向きの白い棒は、狭い勉強部屋でも威力を発揮するレーザーポインタです。
















