サルスベリの本年枝が隣の松や槙に被っているため枝打ちしました。
何気なく葉を観るとサルスベリの葉の裏に幼虫が。

サルスベリは、一昨年カイガラムシの被害を受けました。
詳しく調べていないので定かではありませんが、カイガラムシの一齢期の幼虫かと思います。
秋になり、本年枝を全て剪定した後に消毒する事にします。
サルスベリの本年枝が隣の松や槙に被っているため枝打ちしました。
何気なく葉を観るとサルスベリの葉の裏に幼虫が。

サルスベリは、一昨年カイガラムシの被害を受けました。
詳しく調べていないので定かではありませんが、カイガラムシの一齢期の幼虫かと思います。
秋になり、本年枝を全て剪定した後に消毒する事にします。
先週、『清里でバーベキュー』を投稿しましたが、清里滞在中に撮った庭の植物です。
先ず、地味ですが珍しいところから・・・

タマノカンアオイです。
寒葵(かんあおい)の名の通り、冬の清里の寒さにも良く耐え、冬の氷点下10℃以下の寒さでも青い葉を見せてくれます。

お次ぎはヤマユリです。

百合の中で最大級の花を付けるそうで、茎が花の重みを必死で支えている様に見えます。

採取した種を撒いたら、庭中に広がったとの事です。風土に合った植物は活き活きとしています。
ただ、庭にやってくる鹿が、芽を食べてしまうそうです。
庭は落ち葉が堆積し、足を踏み入れるとフカフカの絨毯の様です。

ここでバーベキューをしました。
おまけで、、、

早朝に、霧の中、清里を後にしたときの写真です。猛暑の川崎に戻ったのでした。
勤務先の夏休みの初日に息子と数学の勉強。
息子が通っている予備校の夏期講習テキストに、またまた受験生が困りそうな問題がありました。
ちっと、文系のレベルを超えていると思い、回答を作ってみました。
S台予備校のテキストでは、「論証」というくくりでまとめられている問題です。
要は、平面上で(x,y)の領域が与えられ、その(x,y)の取り得る条件下で、「x+y」の最大値を求めなさい、、、
という問題です。

たいがい、(x,y)の取り得る「領域」は、受験生にも容易に図示できます。
例えば、「x+y」の最大値を問われれば、
x+y=k
と置き、これを
y=-x+k
と変形し、y切片が「k」で、傾きが「マイナス1」の直線(一次関数)と考え、
平面上に描いた「領域」を、直線が通過するときの最も小さなy切片を求めれば、これが「x+yの最小値」となります。
ところが、このK大の問題で与えられた「領域」は、
x^2 -2xy +2y^2 = 4 ・・・①
で、「-2xy」が邪魔になって、見慣れた楕円の式
(x/a)^2 + (y/b)^2 = 1
に変形できず、「領域」を図示できません。
実は、「xy」項が入ると、下図のように楕円が回転します。
なお、回転した楕円の作図が課題でないため、下図の楕円の傾きは正確なものではありません。
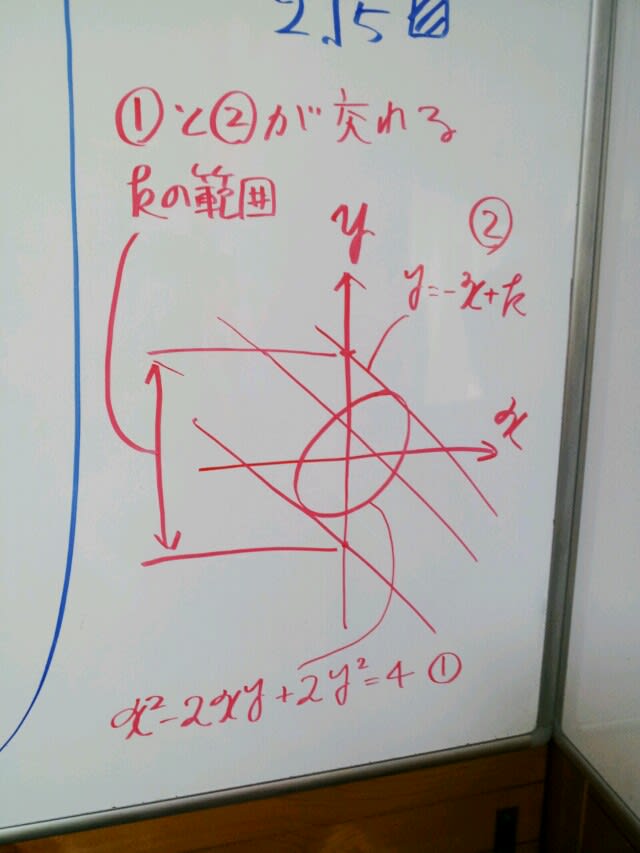
この楕円の作図は、理系でもなかなか出来ないので、どう解こう(汗)、、、となります。
結論は、やり慣れた図形的な検討からの解答ではなく、
x^2 -2xy +2y^2 = 4 ・・・①
に
y=-x+k
を代入して、xの二次方程式(係数にkの式を持つ)とし、判別式をたてます。
判別式≧0
とすると、kの範囲が得られます。
このkの範囲の上限が、「x+y」の最大値となります。めでたし
因に、下が自分用の自宅数学教室用セットです。

パイロットのボードマスターの、「書き味」と「消し味」が気に入り、
ネット通販で、替芯と替えインクをまとめ買いしました。
あと、一本だけ横向きの白い棒は、狭い勉強部屋でも威力を発揮するレーザーポインタです。
受験勉強中の息子のたっての希望で、清里でバーベキューを敢行。
ほとんど、バーベキューをするだけのために清里まで行きました。

炭火の遠火で焼き上がったところです。
肉汁が溢れる様です。

串三本を刺して持つと、結構な重量感。
多めの粗塩、黒胡椒、すりおろしニンニクを塗り込み、串を刺して一休み。

肉に味をなじませている間に、タップリの炭を熾します。

使い込んだバーベキューコンロです。ここまで使えば安いもんです。
肉に厚みが十分にありますので、遠火でじっくり焼く焼き方に耐えます。

焼き上がった肉を休ませて肉汁が落ち着いたところで、厚めにカット。

肉の内側は赤いですが、しっかり熱が入っています。
ステーキというより、ローストビーフに近いです。
一切れを皿に盛り、醗酵バターを添えた、炭焼きのベークドポテト、エリンギとともに戴きました。
赤ワインに良く合います。

とても一切れで済まなかった事を申し添えます。