1つの理由として、そもそも、foldlを使ってtakeやdropを書こう、とかまず思わないだろうと言う事。
つまり、このお題は本質的にはfoldlを使ってフィボナッチ数列を書くお題の類題なんだ。フツーの人が考えないだろうお題となっている。
もう1つは複数の解が考えられて、これ、と言ったスマートな解が(特にtakeに対して)得られない事。
だから複数並べといて「好きなの選んだら?」としか言いようがねぇんだよな、基本的に。
んで、この解を提示した時は、takeとdropの対称性を重視して出したのね。
つまり、結果としてのコードがどうあれ、お互い相互補完的な「発想」になってる、って前提で組み合わせた。
言い換えると最初の例は本当に相互補完的な成功例なんだけど、後者は「発想は相互補完的」だけど、出てきたコードはそうじゃないケース、になってる。なんせtakeにはcall/ccとか見た目余計なモノが付け足されてるしな。
んなわけでちと悩ましい状態だ。
ちとfoldlに付いて整理してみよう。
foldlの形式は一般的にはこう書かれている。
(foldl 関数 初期値 リスト ...)
もうちょっと細かく見てみよう。
(必須ではないにせよ)関数がラムダ式だった場合、fold/reduceは次のような図になっている。
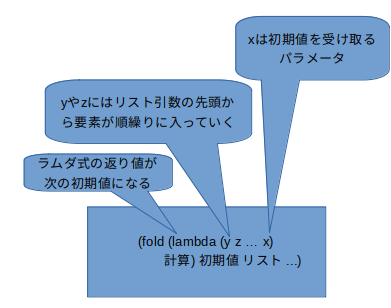
まぁ、曲がりなりにもfold/reduceを使ってると当たり前だろって思うダイアグラムかもしんない。
しかし、恐らく、次の2つはハッキリしていなきゃならないと思うわけだ。
- fold/reduceは仕様上、第一引数に最低でも2引数関数を取るが、ラムダ式本体における計算上、その2引数以上を必ず全部使わなければならないと言う縛りはない。
- fold/reduceは一見、初期値を破壊的に加工してるように見える。しかし、直感に反して、初期値に計算結果を代入しているわけではない。関数型プログラミングの真髄であるfold/reduceには代入のような副作用は含まれていない。そうではなく、ラムダ式の返り値が次の初期値に束縛されているだけ、だ。
この2つは強調しても強調し過ぎる事はないだろう。
特に2番目には留意しておいた方がいい。ラムダ式である計算を行った場合、初期値に例えば「加算」が生じた場合、それはラムダ式の返り値が計算上そうなってる、ってだけの話で、本質的にはfold/reduceが代入してる、ってワケじゃあないんだ。
そして計算にラムダ式の引数を全て几帳面に使わなければならない、ってワケでもない。従って、ちょっとトリッキーに見える計算は、上の2つの留意点に注意すれば氷解する事が多いだろう。
例えば、だ。
(define (last xn)
(car (foldl cons '() xn)))
(define (last-pair xn)
(list (car (foldl cons '() xn))))
これを何故に紹介したのか、と言うとreverseと言う関数がfoldlで組み立てられるからだ。つまり、事実上、この2つの関数は、
(define (last xn)
(car (reverse xn)))
(define (last-pair xn)
(list (car (reverse xn))))
と全く同じだ、っちゅう事だ。
繰り返すが、reverseをfoldlで書くのは基本戦略って言っても良いくらいで、「なぜ関数プログラミングは重要か」と題された文書にも取り上げられている基本中の基本だ(もっともこれはHaskellで書かれてるが)。
しかし実の事を言えば、もっと簡単に書けるのも事実なんだ。上の2つの留意点を考慮すれば、こんな風にも書ける。
(define (last xn)
(foldl (lambda (y x)
y) #f xn))
(define (last-pair xn)
(foldl (lambda (y x)
(list y)) #f xn))
この2つでも望んだ通りの計算になる。
この2つの場合、
- 初期値自体はどーでも良い、と言う態度(なんで何でもいいから取り敢えず #f を与えとけ、と言う投げやりな方針)。
- 計算が行われてないように見える。yはリストxnの先頭から順繰りに値を受け取るわけだが、返り値は基本「受け取ったyをそのまま返してて」、それが次の初期値になる。
- 従ってリストxnを走査し終わった時点で、foldlの返り値は当然リストxnの最期の値になっている。
が過程だ。「ラムダ式が全く計算らしき事してないように見える(なんせ初期値xを使ってないし)」、つまり、リストの値を単に順次初期値に流してるお陰で最期の値がfoldlの返り値になっちまう、と言うあまりにもバカバカしい過程で望んだ結果を得てるわけだ。
foldlは慣れなければならない、関数型プログラミングに於いての最重要関数の1つである、って事は事実だ。それはそれで事実なんだけど、パーツ毎に考えてみると、実は縛りはゆるゆる、ってのも事実なんだよ。「強制的にこうせなアカン」って類いのモンでもない。初期値はどんなデータ型でもいいし(数値、リスト、ベクタや構造体でもいい)、リスト引数なんかもいくつでも取れる。
そして、コントロールを担ってるのはあくまでラムダ式なんだ(foldlが担ってる、ってのは言っちゃえば誤解だ)。
故に、「ラムダ式の書き方を考える」のが一番重要で、と言う事は「何が返り値としてふさわしいのか」考えるのが最重要、って事になる。
foldlが受け取る関数引数は2引数以上じゃないとならない、そしてリスト引数と初期値の位置が直感に反してヘンだ、ってのは事実なんだが、言い換えると、そこだけは「縛り」だが、他は結構フツーの関数と同じだ、って事なんだよな。foldlが持ってる初期値に関数の返り値が束縛されていく、って事だけ押さえておけば、実はあんま考え込まなくても良い、って事になる。
さて、こうやってfoldlを復習しておいて。
まずは散々見た、take & dropの簡単な方、dropから話をはじめよう。
dropは再帰だと次のように書ける。
(define (drop xn n)
(if (zero? n)
xn
(drop (cdr xn) (- n 1))))
カウンター入りのcdr再帰(cdr-downとも言う)の全く基礎的なカタチだ。カウンターが0になったらリストxnを返すだけ、と言う。
これは全然難しくない。ある程度Lispやら、あるいは再帰の書き方に慣れるとハナクソをほじるまでも無く書けてしまう。
さて、これをfoldlで書き直すとしたらどうすればいいんだろう。思いつくのはリストxn自体を初期値として「先頭を削っていく」プロセスだ。
ここで悩むのはリストxnを引数リストにするか、初期値にするか、と言う二択だが、「加工対象が何だろか」と考えれば自ずとからどっちがより良いのか、と言うのは決まるだろう(もちろん別解を考えたい、ってアイディアを妨げるものじゃない)。
そしてカウンターはrangeでリスト化してfoldlでの処理で空リストになった時、計算が終わるようにすれば良い。
つまりこう書けば一番シンプルになる。
(define (drop xn n)
(foldl (lambda (y x)
(cdr x)) xn (range n)))
繰り返すが、foldlは2つ以上の引数を取る関数を第一引数として取るが、その関数本体内で「引数を全部計算に使用しなければならない」と言う縛りはない。
ここでも初期値xn(リスト)をそのまま受け取るxをcdr-downするだけで計算目的としては充分で、ついでにそれが返り値になる以上、次の初期値は(cdr x)になるわけだ。
そして(range n)がプロセスを経て空リストになれば計算終了、って事だ。その時点で必要な数だけ先頭が削られたxnの残りが返され、dropの意図通りの結果になる。
さて、takeとdropはコンビなわけだが、同様の発想をtakeに持ち込もうとすると若干厄介になる。
まずは基本となる再帰版から考えてみよう。
(define (take xn n)
(let loop ((xn xn) (n n) (acc '()))
(if (zero? n)
(reverse acc)
(loop (cdr xn) (- n 1) (cons (car xn) acc)))))
実は「Schemeらしい再帰」として見ると別段難しくはないわけだ。簡単に書けるのは間違いない。
ただし、dropと比べると処理すべき引数が増えている。まずはアキュムレータaccが必要になる。そしてそれを外部に引数として晒したくない場合、名前付きletの助けを借りるのが基本戦略になる。
もう1つの問題は、accにconsしていくせいで、takeが求めるリストの逆順にリストが生成されてしまう、と言う事だ。従って、カウンタが0になった際、accをそのまま返すのではなく、ひっくり返して返さないとならない。そしてreverseは実はそれなりに計算コストがかかる。
consはLispに於いては最重要関数の1つではあるんだけど、reverseを避けてみたいとする。1つのテとしては、appendを利用して
(define (take xn n)
(let loop ((xn xn) (n n) (acc '()))
(if (zero? n)
acc
(loop (cdr xn) (- n 1) (append acc (list (car xn)))))))
と書くテがある。
しかし、どう見てもconsを使った方がスッキリするよな。そして、append使ったから、と言ってappend自体がコストがかからない、と言うわけでもない。
しかしながら、あくまで記述をスッキリさせる為、ANSI Common Lisp由来のこういう書き方を試してみる事が可能だ。
(define (take xn n)
(let loop ((xn xn) (n n) (acc '()))
(if (zero? n)
acc
(loop (cdr xn) (- n 1) `(,@acc ,(car xn))))))
そう、ここに於いて、
(append acc (list (car xn))) ≒ `(,@acc ,(car xn))
だ。後者の書き方に慣れよう。一見「?」と思う記述法だが、簡潔さではこちらが上だ。
後者の書き方の記号的な要素は3つしかない。逆クオート(`)、コンマ(,)、それとコンマ@(,@)の3つだ。
これらはぶっちゃけ、ANSI Common Lispなんかでマクロでリストを組み立てる際に使う記法だった。
しかし、SchemeはANSI Common Lisp方式とは全く別のマクロを採用する事になった。従って、フツーにリストを組み立てる時に使う、しか使い道がなくなっちゃったワケだな(笑)。可哀想なんで使ってあげよう(笑・※1)。
ルールは次のようなモノだ。
- リストを組み立てる際には `() と言うカタチが「大外の」枠組みになる。
- `() 内にあって、コンマに続くシンボルないしはリストは、評価される。
- `() 内にあって、コンマ@に続くリストは、()が消えて中身だけになる(そして各要素は評価される)。
これだけ、だ。
例えば上の例で、現時点accが '() で xn が '(a b c d e f g h) だとしよう。
そうすれば、`(,@acc ,(car xn)) と言うのは、
- ,@acc -> ,@'() だが、カッコが消える。中身がないので結果何もない。
- ,(car xn) は評価されるので'aになる。
結果、その時点では'(a)と言うリストになる。そして再帰的にaccは'(a)と言うリストになる。
次の段階だと、
- ,@acc -> ,@'(a) だが、カッコが消えるので、aだけがポツネン、と出てくる。
- ,(car xn) は評価されるので 'b になる。
結果、'(a b) と言うリストになる。
そしてまた次の段階だと'(a b c) と言うリストが生成され・・・となっていく。
別にだからと言って演算速度が上がるわけじゃないが(※2)、この表記法は「便利」なんで慣れていた方がいい。とにかくリストの中身をバンバン明示的に記述していく方式だ。
人によってはconsを使う事で混乱を生じる人もいるだろうし、ある意味リスト操作としてはこちらの方が明解な可能性さえある。
さて、まずは逆引用符とその仲間の使い方を把握しておいてから、foldl版のtakeをどうするか考えてみよう。
上の再帰版を見た通り、takeはdropに比べるとどうしても1つ引数が増えてしまうだろう事は予想出来る。そして、初期値は、ストレートに考えると空リストになりそうだ、と言う予想になる。
dropとの対比を考えて、直球勝負で書くとしたら次のような定義が考えられるだろう。
(define (take xn n)
(foldl (lambda (y z x)
`(,@x ,y)) '() xn (range n)))
再帰版と同様に、初期値を空リストとし、リスト引数としてxnを採用、そしてついでにrangeでnから作ったカウンター用リストを作る。
これで、カウンター用リストが空リストになった時点で、計算が終わる、と。
至極真っ当だ。
ところが、Racketのfoldlだとエラーが生じるんだよな。
> (take '(a b c d e f g h) 3)
. . foldl: given list does not have the same size as the first list: '(0 1 2)
>
なんと、foldlのリスト引数は全部同じ長さじゃなきゃいけない、と文句を言われる。
だとすると、この直球勝負版は諦めないとならない。
そうすると、僕らが考えうる戦略は、基本的に次の2つとなる。何故なら、初期値、xnリスト、そしてカウンターnの扱いをそれぞれどうすんだ、と言う問題になるからだ。
- xnを引数リストとして、カウンターn と空リストを初期値とする。
- rangeとnでカウンター用リストを作って、空リストとxnを初期値とする。
取り敢えず空リストが初期値の一部を担う事になるだろう、ってのは想像に難くない。問題は (range n) と xn の長さが違うんで、この2つの間でどう帳尻を合わせるか、なんだ。
1番目の方針が、例えば次のようなコードを産み出す。
(define (take xn n)
(call/cc
(lambda (return)
(foldl (lambda (y x)
(let ((count (car x)))
(if (= count n)
(return (cdr x))
`(,(+ 1 count) ,@(cdr x) ,y))))
'(0) xn))))
xnをリスト引数とすると、foldlはxnの最期まで走査しようとする。
そこでcall/ccでカウンターがnと同じになった時、脱出するわけだ。
初期値は '(0) とする。carはカウンターの初期値(0)になりcdrの初期値は '() なのでアキュムレータになる。ここではコードを明確に表現する為、初期値を '(0 . ()) としたが、事実上 (cons 0 '()) は '(0) なので、今回はシンプルさを優先した。
結果、例えば
> (take '(a b c d e f g h) 3)
'(a b c)
>
の場合、初期値は
'(0) -> '(1 a) -> '(2 a b) -> '(3 a b c)
と変遷していく。そしてカウンターが3に達した時継続が働いて、cdrを返して計算終了(と言うか(cdr x)を持って脱出)、と言うわけだ。
2番目の方針に従うとtakeは次のように書ける。
(define (take xn n)
(car (foldl (lambda (y x)
`((,@(car x) ,(cadr x)) ,@(cddr x)))
`(() ,@xn) (range n))))
これでも計算は狙った通りに行われる。
> (take '(a b c d e f g h) 3)
'(a b c)
>
初期値は`(() ,@xn) と記述されてるが、上の例の場合、初期値は
'(() a b c d e f g h)
からスタートしてる。これから
'(() a b c d e f g h) -> '((a) b c d e f g h) -> '((a b) c d e f g h) -> '((a b c) d e f g h)
と推移していき、この時点で (range n) で作られたリストは空リストとなる。
あとはcarを取れば、狙った結果になるわけだ。
この計算過程を見れば、foldlを用いたフィボナッチ数列の計算方法の応用だ、と言う事が分かるだろう。
もう1つの追加の方法論としては、どうしても逆引用符に慣れない、と言う場合、カウンターリストを (range (- (length xn) n)) として、やっぱ逆順で処理して逆順で返り値を返す、と言う方法が考えられる。
(define (take xn n)
(reverse (cdr (foldl (lambda (y x)
(cons (cons (cadr x) (car x)) (cddr x)))
(cons '() (reverse xn)) (range (- (length xn) n))))))
これも計算は正しく行われる。
> (take '(a b c d e f g h) 3)
'(a b c)
>
この場合初期値は '(() (h g f e d c b a)) となってて、
'(() (h g f e d c b a)) -> '((h) (g f e d c b a)) -> '((h g) (f e d c b a)) -> '((h g f) (e d c b a)) -> '((h g f e) (d c b a)) -> '((h g f e d) (c b a))
と処理され、ここで (range (- (length xn) n)) (つまり、リストxnの長さからnを引いた長さで生成したリスト)が空リストになる。そこでcadrを取ってreverseすれば目的が達成出来るわけだ。
ただし、最初の2つに比べると冗長なのは否めないだろう。consもreverseもしまくり、ってのも計算効率を悪くしてる。
繰り返すが、逆引用符とそれに纏わるコンマ、コンマ@を使用した方が表現に幅が出て、また短く書くことが可能だ、と言う事を実感して欲しい。如何にも「記号」と言う表記法だけど、それが故にパワフルなのも事実なんだ。
なお、実の事を言うと、SRFI-1のfoldは、引数リストを複数取って、それぞれの長さが違っても問題がない。一番短いリストが消費され終わった時点で計算が終わるので、従って、Racketがエラーを返した「直球勝負の例」が一番スマートだ、って事になる。
(require (only-in srfi/1 fold))(define (take xn n)
(fold (lambda (y z x)
`(,@x ,y)) '() xn (range n)))
実は、この「リスト引数の長さの扱いの違い」というのが、Racket組み込みのfoldlと、SRFI-1のfoldの違いなんだ。
よって、オチを言うと、面倒臭い記述や計算の回避を狙うのなら、Racketのfoldlを使うよりSRFI-1のfoldを使った方がいい、と言う事にはなるだろう。
※1: ここで練習しておけば、ANSI Common Lispでのマクロ記述でも悩まなくて良いだろう。実際問題、ANSI Common Lispのマクロで最初、何に一番悩むかと言うと、逆引用符絡みの記述だ。
※2: 平たく言うと、逆引用符もコンマもコンマ@もマクロだ。
ただ、ANSI Common Lispの場合は、プログラミング言語としては珍しくコンパイラが定義されていて、マクロは展開されるものだが、コンパイル時に完全に展開される事となる。つまり、事実上、ソースコードがマクロに従って書き換えられる、と言う事で、これにより、「演算に頼らず」結果の式が完全にベタ書きされるような状態となり、結果演算速度が上がる事となる。
一方、Schemeはフツーのプログラミング言語と同じようにコンパイラはない。正確に言うとコンパイラは仕様上定義されていない。従って、マクロが返す「計算結果」は「あるカタチになる」と保証されているが、ANSI Common Lispのように「計算速度が上がる」と言う保証は成されていない。その辺は「実装依存」と言う事となるだろう。














