龍虎氏の記事(2024/02/07)についてのコメント。
解説を読んでも全然ついていけなかったので今回は最初から解答例を拝見する。Case-lambda?わっ?なんだこの書き方は・・と思ったけど、なるほど・・これはスマート。Unfoldは、終了条件、手続き、ステップ、初期値って感じかな
そうそう、SRFI-1のunfoldの説明はそういう事です。
- p => 終了条件
- f => 手続き
- g => ステップ
- seed => 初期値
まさしくその通り、です。
うーん、込み入って見える!あと地味に数値の入力は(read)で良かったと今更知る。いつも(string->number (read-line)でやってましたw
思わず笑っちまったけど(笑)、正しい。
っつーか龍虎氏はいつの間にか立派なソフトウェアエンジニアになってるっぽい(笑)。
そうじゃなくてもゲームプログラマだ(笑)。
そうなんだよね。Lispのreadは完全なLispパーザを備えてるんで、ゲームでそのまま使うにはあまりに危険な代物なんだ。自作ゲームプログラムなのに任意のLispコードを実行出来てしまう危険性がある。
よって、readをそのまま使う、と言うのは避けるように、と言うのはLand of Lispにも記載されている。
従ってread-lineをstring->numberで包む、ってのは全く正しい。もうゲームばっかプログラミングしてて、ソフトウェア制作上のそういうマナーが自然と身についてる状態になっちまった、っつー事だ。
もう龍虎氏は汚れちまったんだよ(笑)。あの素朴で純粋だった龍虎氏はもはやどこにもいないのだ(笑)。
骨の髄まで「ソフトウェアプログラミング作法」に毒されている(笑)。
Log? ということでココからは明日頭がスッキリしてから考えることにしよう。
対数だね。高校数学だ。
多分、ここ、Pythonのリスト内包表記でも引っかかってたかも。
んで、確かに、三角関数に比べても出番があんまねぇんだよな(苦笑)。
以前書いたかもしれないけど、対数を使う一番有名なプログラムは階乗計算だ。
いや、これもLispは「どんな大きな数でも扱える」んで、あんまピンと来ないんだよな。
そのまま書き下して書けちゃう。そして再帰計算の例として出まくりだ。
(define factorial
(case-lambda
((n acc)
(if (zero? n)
acc
(factorial (sub1 n) (* acc n))))
((n)
(factorial n 1))))
Lispは凄い。こんなデカイ数でも計算してくれる。
> (factorial 10)
3628800
10の階乗で三百六十二万八千八百だ。7桁の数値に達する。
ところが、Lispだからこうなんだけど、他の言語、例えばC言語なんかではこんなデカイ数を扱うプログラムは簡単には書けない。
なんせ、扱える整数の「範囲」ってのが、ハードウェアに左右されはするけど、決まってるんだよ。「上限値」ってのがある。
んでそういう場合、「小さい数」に変換して計算する。そういう時使うのが対数なんだ。
階乗の定義は以下のようなモノだ。
n! = n × (n - 1) × (n - 2) × ・・・・・・ × 2 × 1
結果、Lispなんかではバカ正直に「このまま」プログラミングしてる。
一方、「対数変換」と言う方法があって、上式の式の両辺の対数を取る。
log|n!| = log|n × (n - 1) × (n - 2) × ・・・・・・ × 2 × 1|
ここで、
log|a × b × ...| = log|a| + log|b| + ...
と言う変換規則(公式)によって右辺は「対数の和」へと変換される。
log|n!| = log|n| + log|n - 1| + log|n - 2| + ・・・・・・ + log|2| + log|1|
んで計算機が無かった時には、対数表、ってアンチョコを使って右辺の値を足し上げてたんだよな(笑)。
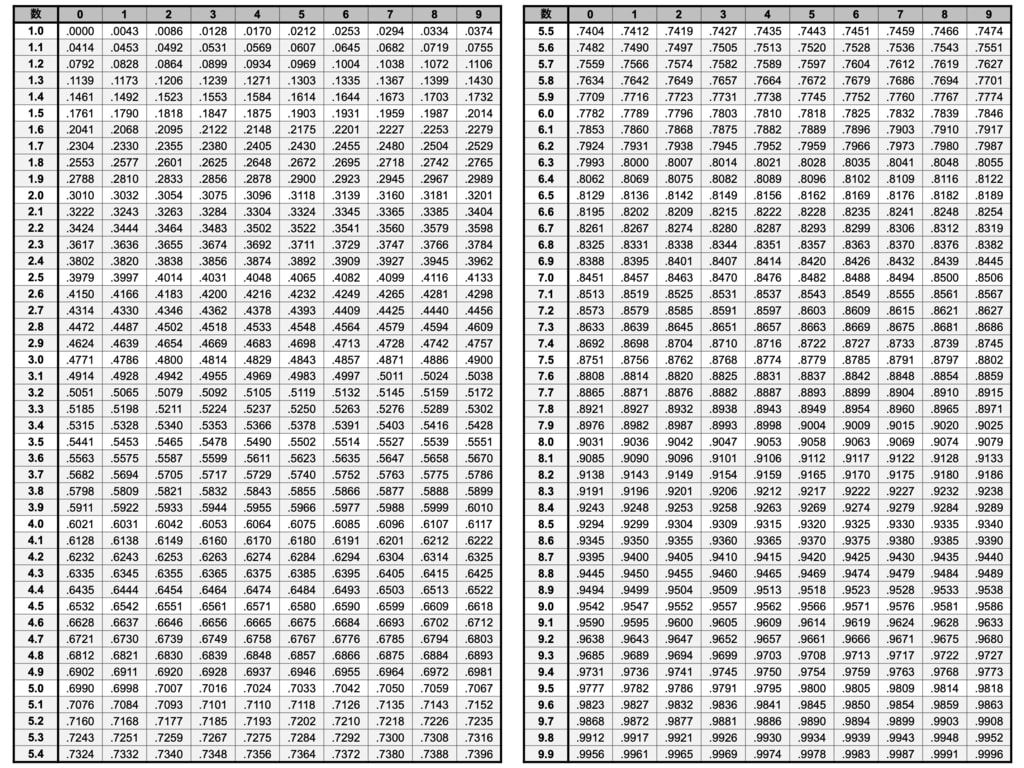
対数表の例
この表で着目して欲しいのが表内にある数はどれも小数点以下の数だ。言い換えると整数を対数に変換するともんの凄く小さな数が生じる、って事だ。
結果、C言語みたいな整数の上限値が厳しいプログラミング言語でも扱いやすい。
また、上の階乗の対数による変換式を見たら分かるけど、計算さえ掛け算から足し算へと変換されている。んで、確か、CPUなんかも掛け算より足し算の方がスピードが速かったんじゃないかな・・・。
結果、C言語みたいに「効率重視」なプログラミングを求めるとすると、「整数を掛けていく」より「浮動小数点数を足していく」方が望ましいわけ。
多分、「対数を使ったプログラミング」で尤も有名なのは、この階乗計算だと思う。他じゃ、数学的スクリプト以外ではほぼ登場しねぇ気はするけどね(笑)。
※: 例えば、階乗の対数を取るプログラムはRacketでは次のように書ける。
(define log-factorial
(case-lambda
((n acc)
(let ((m (log n)))
(if (zero? m)
acc
(log-factorial (sub1 n) (+ acc m)))))
((n)
(log-factorial n 0))))
(factorial 10) は3628800だった。
一方、log-factorialを使うと
> (log-factorial 10)
15.104412573075514
解は15程度だ。定数ではないが、10の階乗ではおよそ240,248分の1、の圧縮率だ。
もちろん、このままでは「階乗です」とは言えないんで、例えば
> (exp 15.104412573075514)
3628799.999999996
として「元に戻す」。対数が「圧縮」だとすれば、ここでデータを「解凍」して元に戻すわけだ。
あとは四捨五入でもすれば3,628,800と言う目的とする数が得られる。
















