龍虎氏の記事(2024/02/08)に対するコメント。
なんでLogが登場するの?ということでClaude先生にお聞きする。
なるほど〜・・3を底にして10000のLogを取る?事で累乗の限界値が分かるから・・うーん、数学的素養が無い僕には絶対に出てこない発想。
いや、大した事じゃないのよ。3 ^ x = 10000を満たすxを探せ、ってだけの話で。

の関係がある。ここまでは「計算」と言うより記号の変換、って事だよな。
んで、具体的には
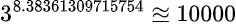
だ。3の8乗は6,561だけど3の9乗は19,683で10,000を超える。って事は、問題に従うと8が整数の上限値、って事になる。
そんだけ。大した理屈があるわけでもない。
ところで、上の2つが同じ結果になるのが不思議なので
いやもうここは公式。

右辺は分子、分母の対数の底(c)が揃っていたら任意でいい。10だろうが20だろうが成り立つ、って言ってるわけ。
んでこれは公式だから暗記でいい。「理由なんて考えなくていいんだ」(笑)。
ドラゴン桜的にはこうだ(笑)。

と言う事だ(笑・※1)。
なお、だから、

これの後半は嘘八百だ(笑)。具体的には5以降はうそっぱちだ。
先にも書いたけど
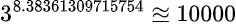
であって、3の4乗は10,000なんかにはならない(笑)。3の4乗は81だ(笑)。
だから何言ってんだかサッパリで、当然、
これ何を言ってるんだろう?10000は10の4乗だと思うんだが?
となる(笑)。
まあ、なんか知らんけど(/ (log 10000) (log 3)) = (log 10000 3) 1となる法則があるんだな。へぇ〜・・
まぁ、上にも書いたけど、法則、と言うより単なる公式かな(※2)。
ふーん、今ひとつピンと来ないな〜なんだよd/dx とかlnって・・これは前にPythonde学び直す高校数学の続きをやらんといかんな〜
ちょっと色々錯綜してるかも。
まず、d/dxから行ってみよう。これは微分記号だ。dy/dxは「yをxで微分する」と言う意味になる。
で、だ。自然科学でネイピア数eが愛用される最大の理由は、単に「微分しやすいから」だったりする(笑)。
こういうルールがあるのね。

ネイピア数のx乗は何度xで微分してもネイピア数のx乗なの。こういう金太郎飴のような特性があるんで、色々と扱いやすいんだわ、数理的に。
そんなわけで、自然科学では、ネイピア数を底にした対数(自然対数)を愛用する。
まずそういう「自然科学での背景」を覚えておこう。
一方、文系。特に経理とか商学の方だよな。
例えばこっちは、10,000円とか一億円とか、やっぱり十進法の世界なんだよ。そしてそういう「お金」の世界では、十進法が基礎なんで対数の底にネイピア数なんかを使う事はあり得ないのね。こっちの世界じゃネイピア数は「不便」だから。結局、対数を扱うにせよ、10が基本の方が都合がいいわけ。「文系」ではそういう背景になる。
んで、10を底とした対数を、通称常用対数と言う。
さて、自然科学では自然対数を使い、文系では常用対数を使う。
んでだ。
毎回毎回log eとかlog 10って書くのがメンドイわけじゃない。つまりここで省略記法の話が出てくるわけだ。
んで、自然科学の方での自然対数の省略記法、文系の方での常用対数の省略記法、ってのが日本では、少なくとも僕らが高校生くらいだった時には全く同じだったんだわ。両者共に底を省略して単にlog 何とか、と書く、と。
だから文系の目で見てlogだけ書かれてれば「底が10なんだな」と解釈し、理系なら「底がeなんだな」とコンテクストで判断してたわけね。
でも僕らが高校生くらいの時、ってのは確か常用対数の方が強かった。高校数学でも「底を省略して書いた時は底が10って意味ですよ〜」とか言ってた気がする。この辺、高校数学でも10年毎くらいでチマチマ変わってた筈なんだけど、最近でも「底が省略された時は10と解釈する」になってたんじゃないかな。
ところが。
アメリカなんかだと、底が省略された時は基本、常用対数って解釈するんだ。そしてネイピア数が底の時、表記法が変わって、それをlnと書く。日本みたいに「同じ表記」じゃないんだ。
そう、lnってのは「自然対数」の事なの。だからそのAI?アメリカ製だろ、多分(笑)。だから表記が揺れている。
なお、lnってのはフランス語のlogarithme naturel(自然対数)の頭文字を取った略称なんじゃないか、って言われている。アメリカって英語原理主義なんだけど、どういうわけだか知ってる範疇だとこれと、あとは線形代数に出てくる固有値と固有ベクトルだけは外国語なんだ(後者はドイツ語で「固有:eugen」を使ってる)。
いずれにせよ、lnって表記は日本じゃあまりメジャーじゃない。アメリカ帰りの大学の先生がちらっと使う程度なんじゃないかしらん。数学の書籍、なんか見ても、日本の本だとまずlnって表現は出てこないよね。
と言う辺りで以下の方の疑問にも答えられたかな。
あと、グラフのプロットとか、視覚的に見て「良く分からん結果」に見えた時、データを対数変換してプロットすると直線に近くなってスッキリする、ってのも良くある。人間って曲線が嫌いなんだよ(笑)。逆に直線だと嬉しくなる。
例えば、なんかのデータを集めてきて、散布図作った際に、その縦軸と横軸の関係が

になってました、ってのは意外と判定が難しいんだ。中学校で習うような式なのにね。
一方、データを弄くって

と変換出来れば中学校で習う「直線の方程式」になってスッキリするわけ。
こういうカンジで、対数は「物事を簡単にして見せる」と言う性質があるんだ。人間は直線が好きだからね。
そんなカンジかな。
※1: 無茶苦茶な意見に思う人もいるだろうが、存外当たってる。
と言うのも、有名な数学者、ラマヌジャンなんかは「いろんな事が天啓みたいにひらめいてくる」らしく、別に「理論的に考えてた」わけではない、と言う実例があるからだ。
僕らは数学の天才にはなれないが、一方、暗記で済むのならそっちで対応しても充分だと思われる。
文句を言ってくるヤツには「ラマヌジャンになりたくて」とかワケの分からん事を言っておこう(笑)。
※2: 歴史的な経緯により「☓☓の法則」と名付けられるモノもあるが、実は数学には「法則」はない。
理学的な意味での「法則」ってのはざっくばらんに言うと、最終的には「経験則」を指す。「今までの経験から言うと☓☓は正しいらしい」と言うモノに対して「法則」と言う言葉を使うわけだ。
数学はそもそも「経験上☓☓だからこうです」とか言う学問ではないので、全く「法則」が介在しないジャンルなんだ。
なお、物理学は「ある仮説を採用して」経験則を数学的に証明する学問、と捉える事が出来る。言い換えると経験則を数理的に上手く証明出来ない「仮説」は役に立たない、と言う事になる。
そして、仮に仮説が経験則を上手く証明したにせよ、「絶対的にその仮説が正しい」、つまり「真だ」とは証明出来ないんだ(仮に他の仮説が「上手く経験則を数理的に証明」しちまったら、「どっちが正しい」と言う問は無意味、となる)。
仮説に仮説を重ねて数理証明に挑むのが物理学、と言う学問だ。














