
「アインシュタイン方程式を読んだら「宇宙」が見えた:深川峻太郎」(Kindle版)
内容紹介:
オレだって数式が読めるかっこいい男になりたい! 微積分も知らずに、男(50代・文系)は数式世界の最高峰「アインシュタイン方程式」をめざし旅立った。「捜さないでください」と書き置きを遺して。
予定調和なしの決死行を見守りながら相対性理論の「真髄」を体感できる、(おそらく)世界初の数式ドキュメンタリーここに誕生! 理論物理学のトップランナー、大栗博司氏、村山斉氏も熱く推薦!
2021年5月21日刊行、272ページ。
著者について:
深川峻太郎(ふかがわ・しゅんたろう)
Twitter: @DeeeeepR
ライター、編集業。1964年北海道生まれ。2歳から東京で育つ。早稲田大学第一文学部文芸専修卒業。2002年に『キャプテン翼勝利学』(集英社文庫)でデビュー。以降、『月刊サッカーズ』(フロムワン)、『わしズム』(幻冬舎、小学館)、『SAPIO』(小学館)などで時事コラムを連載。本名(岡田仁志)では著書に『闇の中の翼たち ブラインドサッカー日本代表の苦闘』(幻冬舎)があるほか、フリーの編集スタッフとして手がけた書籍は200点を超える。編集協力した『宇宙は何でできているのか』(村山 斉著/幻冬舎新書)は新書大賞2011、『大栗先生の超弦理論入門』(大栗博司著/講談社ブルーバックス)は第30回講談社科学出版賞を受賞。
理数系書籍のレビュー記事は本書で460冊目。
書店でこの本を見かけたとき「あれ、相対性理論の入門書がまた出たのか!」と思ったのが第一印象だった。講談社ブルーバックスだけでもこのシリーズが1963年に創刊して以来、いちばん多く取り上げられたテーマで、それはAmazonで検索するとすぐわかる。
「相対性理論」というキーワードで: ブルーバックス本を検索
「時空」というキーワードで: ブルーバックス本を検索
名著、良書が乱立する中で、新しい本を出すのは相当の覚悟がいるのではないか?どのように棲み分けをするのか?とつい思ってしまう。僕はこの理論をすでに理解しているからあえて読む必要はないのだが、気になってしかたがない。誘惑に負けて手を出してしまった。
読み始めてすぐ本書が「買い」だとわかった。数式がわからない「ド文系の」著者が、物理学を専門としている「しょーた君」に教えてもらいながら、数年かけて相対性理論を一歩一歩学んでいった過程を記録したものだ。これはさながらドキュメンタリーであり、著者は「冒険」と表現している。本書は企画してから刊行するまで6年かかっている。
特殊相対性理論であれば、科学雑誌のNewtonでも数式導出を含めて説明できるが、一般相対性理論のアインシュタイン方程式までとなると無理である。そしてブルーバックスのような小型本では、とうてい無理だと僕は思っていた。それが本書で覆された。
アインシュタインとは質量によって時空が歪むことをあらわす次のような式である。
アインシュタイン方程式(左辺は時空の曲がり具合、右辺は物質の分布)
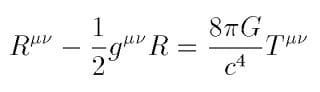
この式のおかげで重力波やブラックホールが予言され、実際に見つかったことはあまりにも有名だ。(参考記事:「重力波の直接観測に成功!(2015年)」、「史上初!ブラックホールを撮影し、その存在を証明(2019年)」)
本書は科学ブログ仲間のT_NAKAさんもお読みになり、たまたま今朝「『アインシュタイン方程式を読んだら「宇宙」が見えた』を読んでみた。」(T_NAKAの阿房ブログ)という素晴らしい紹介記事を投稿されている。
著者の深川さんは「ド文系」といっても、フリーの編集スタッフとして手がけた書籍はこれまでに200点を超える。つまり数式無しであれば、科学教養書を執筆できる実力を持った方である。深川さんが編集協力した『宇宙は何でできているのか』(村山 斉著/幻冬舎新書)や『大栗先生の超弦理論入門』が含まれている。著名なこのお二人の先生から、本書には次のお言葉をいただいている。(すごいことだ!本の帯に両先生のお名前と推薦文を載せてもらえるなど、著者は幸せ過ぎる!)
★大栗博司(カブリ数物連携宇宙研究機構機構長)
物理学の最高峰「一般相対性理論」に徒手空拳で挑んだ冒険譚を読み、私の学生時代の勉強を思い出した。数式の吹雪の中で遭難しそうになりながらも登り続けるところにリアリティがある。
★村山 斉(カブリ数物連携宇宙研究機構初代機構長)
バカボンのパパから岡本太郎、峰不二子までが出てくる物理学の本はまずない。数学嫌いによる、宇宙の言葉=数式への果敢な挑戦。山登りのような達成感を、読者も実感だ!
僕がアインシュタイン方程式を理解できたのは2007年に「時空の幾何学:特殊および一般相対論の数学的基礎」という幾何学的視点から書かれたユニークな教科書で学んだときだ。この本は、たまたま今月新装版が復刊している。僕が独学で理解できたのは、数学は好きで大学の専攻も数学だったからだ。
アインシュタイン方程式を学ぶ過程は、登山にたとえられる。そしてその勾配は富士登山のように頂上に近づくにつれて傾斜が急になる。(難易度が上がる。)アインシュタイン方程式にたどり着くまでの大まかな流れを広江克彦さんの「趣味で相対論」を例にとって解説したのが「一般相対性理論に挑戦しよう!」という2009年に書いたブログ記事だった。本書の流れもこの記事とだいたい同じである。
本書の章立ては、次の通りだ。
プロローグ 宇宙が「数学の言葉」で書かれているのなら
(準備の部)
第1章 ガリレオの相対性原理
第2章 時間の延びとローレンツ変換
第3章 距離と時間と不変間隔
第4章 4元ベクトルとE=mc^2
(登山の部)
第5章 一般座標変換と共変微分
第6章 リーマン曲率テンソルとメトリック
第7章 測地線方程式とエネルギー・運動量テンソル
第8章 アインシュタイン方程式
エピローグ 方程式を「読む」「解く」ということ
これが深川さんの「冒険」の順番であり、本書の構成は次の杉山先生の相対性理論の教科書にならっている。本書ではまた、須藤先生の教科書も参考にされている。(この他、巻末の参考文献が素晴らしい。)
「相対性理論 (講談社基礎物理学シリーズ):杉山直」(Kindle版)
「一般相対論入門 改訂版:須藤靖」(Kindle版)


本書を読めば著者が数年かけて学んできた驚きや感動をを追体験できる。空間が、そして時空が歪むのがどういうことなのかを数式で理解することでよりリアルに実感することができる。T_NAKAさんがお書きになっているように、本書はアインシュタイン方程式を数式で解説している「もっともページ数が少なく、安価な本」なのだ。
しかし、本書を読めばド文系の初学者がアインシュタイン方程式を理解できるというわけではない。あくまでも追体験して概要をつかむことができるレベルまでという限界があるのを承知していただきたい。(それでも感動できるはず。)
初学者は初めて見る専門用語をとかく誤解しがちだ。物理法則の共変性と共変ベクトルでは「共変」の意味が違うし、共変ベクトル・反変ベクトルがあり、共変微分があるのなら反変微分もあるのだろうなどと思ったりもする。本書を読めば、少なくともそのような誤解で無駄な時間を使うことを避けることができる。
テンソルやリーマン幾何学も、数学書で学ぶと挫折しがちだが、本書で概念をつかんでおいてから、他の教科書で詳しく学ぶとよい。また本書で「メトリック」と書かれているのは他の本では「計量」と書かれていることが多い。
アインシュタイン方程式を学ぶとき、初学者が上で紹介した杉山先生や須藤先生の本のような「教科書」で独学するのは無理だと僕は思っている。
というわけで、本書を読み終えて独学で学んでみたいと思うなら「ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平」や「趣味で相対論:広江克彦」(無料で学ぶのであれば「EMANの相対性理論」)のような副読本のほうがよいと思う。そして分厚い本でも大丈夫という方には「一般相対性理論を一歩一歩数式で理解する: 石井俊全」をお勧めする。
ぜひ、チャレンジしていただきたい。
以下は著者による、本書の紹介文である。
【この無謀な願望が、すべてのはじまりだった】
嗚呼、わかりたい。ちょっとでいいから、数式で宇宙がどう書かれているのかをわかってみたい──そう思うのが人情だろう。だって、彼らは自分と同じ人間なのだ。しかも間違いなく、ものすごく面白いことを研究している。ならば、交流したいじゃないか。カタコトでいいから、同じ言葉でお喋りしてみたいじゃないか。それはもう、外国旅行から帰国するやいなや「やっぱり英語できるようになりたい!」と駅前留学しちゃうような気分である。(プロローグより)
【著者の苦闘を見物するうちに相対性理論の真髄が見えてくる】
・数式だからわかる、時間と空間に代わる「不変なもの」
・こうすれば「時間の延び」が計算できる
・E=mc2はどのように導けるのか ・アインシュタインはグニャグニャな空間といかに戦ったか
・時間と空間が「混じる」とはどういうことか ・「行列のお化け」テンソルとは何者か
・ブラックホールの解はいかに導けるか ・ここだけの話、数式は飛ばして文章と絵だけでも楽しめます
関連ページ:
本書の『プロローグ 宇宙が「数学の言葉」で書かれているのなら』『(準備の部)第1章 ガリレオの相対性原理』までは、次のページで読むことができる。
アインシュタイン方程式を読む ド文系が挑む「一般相対性理論」への道
第1回 数式を知らずして、宇宙がわかるものか!
第2回 読み方すらわからない
第3回 これが行列の化け物「テンソル」だ!
第4回 「出発前の準備」が特殊相対性理論
第5回 あんがい簡単だった「ガリレイ変換」の式
第6回 微分は「わかったつもり」になって進もう
関連記事:
一般相対性理論に挑戦しよう!
https://blog.goo.ne.jp/ktonegaw/e/ea7ad9292ce01ad4abbbc8c98f3303d0
趣味で相対論(EMANの物理学):感想
https://blog.goo.ne.jp/ktonegaw/e/5fe7d774a955f3bb9d8270f6113e453f
ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平
https://blog.goo.ne.jp/ktonegaw/e/f4401f2ce79451070b7b9c089f304315
発売情報:一般相対性理論を一歩一歩数式で理解する: 石井俊全
https://blog.goo.ne.jp/ktonegaw/e/1699a1c22477c269c68c02091d0ca049
発売情報: 重力(上)(下) アインシュタインの一般相対性理論入門: ジェームズ・B・ハートル
https://blog.goo.ne.jp/ktonegaw/e/c195a49914a852b1c73049bb7b9743e0
時空の幾何学:特殊および一般相対論の数学的基礎
https://blog.goo.ne.jp/ktonegaw/e/ffc643a688ce45dec7460d107fe1392e




「アインシュタイン方程式を読んだら「宇宙」が見えた:深川峻太郎」(Kindle版)

プロローグ 宇宙が「数学の言葉」で書かれているのなら
- 「タテガキのサイエンス」の役割
- われわれも「数学の言葉」で書かれている
- これは「冒険」である
(準備の部)
第1章 ガリレオの相対性原理
- あちこちに顔を出す「μν」の謎
- 最初の衝撃
- R^μνには巨大な中身があった!
- 「登山前の準備」が特殊相対性理論という現実
- ガリレオの「相対性原理」とは?
- 「ガリレイ変換」の式はあんがい簡単だった
- 異なる慣性系の「F=ma」が同じになるか
- とうとう登場しやがった微分記号
- 「d」がついたら「瞬間的な変化量」のこと
- 力の本質は加速度だった!
第2章 時間の延びとローレンツ変換
- ニュートン力学と電磁波の矛盾
- 16歳のアインシュタインの思考実験
- 物理学は妥協を許さない
- 暴かれたニュートン力学の限界
- ミンコフスキー時空図で時空を深く理解する
- 「同時」は慣性系によって異なる!
- 謎の係数「κ」を求めるのだ
- ローレンツ係数「γ」も求めるぞ
- ああ美しきローレンツ変換
第3章 距離と時間と不変間隔
- 「光速度一定」なら時間は延びて距離は縮む
- 時間や距離に代わる「不変な何か」とは
- 線形代数入門
- 相対性理論に欠かせない概念「不変間隔」
- 偏微分との出会いに目を回す
- 「Σ」で数式をおかたづけ♪
- どこに行くんだこの計算は!?
- そして教科書は真っ黒になった
第4章 4元ベクトルとE=mc^2
- アインシュタインが決めた「オレ様ルール」
- 4次元時空ではベクトルの「変換性」はどうなる
- ミンコフスキー・メトリック
- 「反変ベクトル」と「共変ベクトル」
- 「逆行列」で反変と共変をチェンジ!
- 「固有時間」が常識中の常識だと?
- 4元速度から「4元運動量」を求める
- 線形代数入門パート2
- いざ中学理科の復習からE=mc^2へ
(登山の部)
第5章 一般座標変換と共変微分
- 「特殊」から「一般」へ
- 等価原理はこうしてできた
- 「潮汐力」こそが重力の本質
- アインシュタインも苦しんだ
- 出た、一般座標変換!しかし
- いよいよ「テンソル」とご対面
- スカラーとベクトルとテンソルの関係
- ベクトル場の微分がテンソルにならない
- 「共変微分」のおかげで「接続」できました
第6章 リーマン曲率テンソルとメトリック
- ユークリッド幾何学からリーマン幾何学へ
- リーマン曲率テンソルは添え字が4つ!
- グニャグニャな時空のメトリック
- 接続がクリストッフェル記号になるとき
- リッチ・テンソルと「ビアンキの恒等式」
第7章 測地線方程式とエネルギー・運動量テンソル
- この段階でまさかの「積分入門」
- 「最小作用の原理」のせいで遠回り
- 「オイラー=ラグランジュ方程式」に癒される
- 測地線方程式は3通りもある、らしい
- お次は「ポアソン方程式」だってよ
- 「発散」するのはストレスだけでいい
- 重力場のポアソン方程式と万有引力
- おそるべし、エネルギー・運動量テンソル
- 「完全流体でOK」という朗報
第8章 アインシュタイン方程式
- 頂上までの道のりを再確認する
- 左辺の係数「a」と「b」
- 右辺の係数「κ」
- これまでの成果を次々に使うのだ!
- 最終アタック
エピローグ 方程式を「読む」「解く」ということ
- 敗北感と達成感
- 「内側」から方程式を読む
- 数式の予言が当たったことの驚き
- 一般的な解法は存在しない!
- これがシュヴァルツシルト解だ!
- 天才の偉業に「あたりまえ」などない
あとがき
参考文献
さくいん
内容紹介:
オレだって数式が読めるかっこいい男になりたい! 微積分も知らずに、男(50代・文系)は数式世界の最高峰「アインシュタイン方程式」をめざし旅立った。「捜さないでください」と書き置きを遺して。
予定調和なしの決死行を見守りながら相対性理論の「真髄」を体感できる、(おそらく)世界初の数式ドキュメンタリーここに誕生! 理論物理学のトップランナー、大栗博司氏、村山斉氏も熱く推薦!
2021年5月21日刊行、272ページ。
著者について:
深川峻太郎(ふかがわ・しゅんたろう)
Twitter: @DeeeeepR
ライター、編集業。1964年北海道生まれ。2歳から東京で育つ。早稲田大学第一文学部文芸専修卒業。2002年に『キャプテン翼勝利学』(集英社文庫)でデビュー。以降、『月刊サッカーズ』(フロムワン)、『わしズム』(幻冬舎、小学館)、『SAPIO』(小学館)などで時事コラムを連載。本名(岡田仁志)では著書に『闇の中の翼たち ブラインドサッカー日本代表の苦闘』(幻冬舎)があるほか、フリーの編集スタッフとして手がけた書籍は200点を超える。編集協力した『宇宙は何でできているのか』(村山 斉著/幻冬舎新書)は新書大賞2011、『大栗先生の超弦理論入門』(大栗博司著/講談社ブルーバックス)は第30回講談社科学出版賞を受賞。
理数系書籍のレビュー記事は本書で460冊目。
書店でこの本を見かけたとき「あれ、相対性理論の入門書がまた出たのか!」と思ったのが第一印象だった。講談社ブルーバックスだけでもこのシリーズが1963年に創刊して以来、いちばん多く取り上げられたテーマで、それはAmazonで検索するとすぐわかる。
「相対性理論」というキーワードで: ブルーバックス本を検索
「時空」というキーワードで: ブルーバックス本を検索
名著、良書が乱立する中で、新しい本を出すのは相当の覚悟がいるのではないか?どのように棲み分けをするのか?とつい思ってしまう。僕はこの理論をすでに理解しているからあえて読む必要はないのだが、気になってしかたがない。誘惑に負けて手を出してしまった。
読み始めてすぐ本書が「買い」だとわかった。数式がわからない「ド文系の」著者が、物理学を専門としている「しょーた君」に教えてもらいながら、数年かけて相対性理論を一歩一歩学んでいった過程を記録したものだ。これはさながらドキュメンタリーであり、著者は「冒険」と表現している。本書は企画してから刊行するまで6年かかっている。
特殊相対性理論であれば、科学雑誌のNewtonでも数式導出を含めて説明できるが、一般相対性理論のアインシュタイン方程式までとなると無理である。そしてブルーバックスのような小型本では、とうてい無理だと僕は思っていた。それが本書で覆された。
アインシュタインとは質量によって時空が歪むことをあらわす次のような式である。
アインシュタイン方程式(左辺は時空の曲がり具合、右辺は物質の分布)
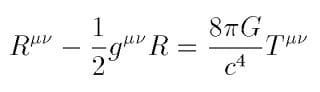
この式のおかげで重力波やブラックホールが予言され、実際に見つかったことはあまりにも有名だ。(参考記事:「重力波の直接観測に成功!(2015年)」、「史上初!ブラックホールを撮影し、その存在を証明(2019年)」)
本書は科学ブログ仲間のT_NAKAさんもお読みになり、たまたま今朝「『アインシュタイン方程式を読んだら「宇宙」が見えた』を読んでみた。」(T_NAKAの阿房ブログ)という素晴らしい紹介記事を投稿されている。
著者の深川さんは「ド文系」といっても、フリーの編集スタッフとして手がけた書籍はこれまでに200点を超える。つまり数式無しであれば、科学教養書を執筆できる実力を持った方である。深川さんが編集協力した『宇宙は何でできているのか』(村山 斉著/幻冬舎新書)や『大栗先生の超弦理論入門』が含まれている。著名なこのお二人の先生から、本書には次のお言葉をいただいている。(すごいことだ!本の帯に両先生のお名前と推薦文を載せてもらえるなど、著者は幸せ過ぎる!)
★大栗博司(カブリ数物連携宇宙研究機構機構長)
物理学の最高峰「一般相対性理論」に徒手空拳で挑んだ冒険譚を読み、私の学生時代の勉強を思い出した。数式の吹雪の中で遭難しそうになりながらも登り続けるところにリアリティがある。
★村山 斉(カブリ数物連携宇宙研究機構初代機構長)
バカボンのパパから岡本太郎、峰不二子までが出てくる物理学の本はまずない。数学嫌いによる、宇宙の言葉=数式への果敢な挑戦。山登りのような達成感を、読者も実感だ!
僕がアインシュタイン方程式を理解できたのは2007年に「時空の幾何学:特殊および一般相対論の数学的基礎」という幾何学的視点から書かれたユニークな教科書で学んだときだ。この本は、たまたま今月新装版が復刊している。僕が独学で理解できたのは、数学は好きで大学の専攻も数学だったからだ。
アインシュタイン方程式を学ぶ過程は、登山にたとえられる。そしてその勾配は富士登山のように頂上に近づくにつれて傾斜が急になる。(難易度が上がる。)アインシュタイン方程式にたどり着くまでの大まかな流れを広江克彦さんの「趣味で相対論」を例にとって解説したのが「一般相対性理論に挑戦しよう!」という2009年に書いたブログ記事だった。本書の流れもこの記事とだいたい同じである。
本書の章立ては、次の通りだ。
プロローグ 宇宙が「数学の言葉」で書かれているのなら
(準備の部)
第1章 ガリレオの相対性原理
第2章 時間の延びとローレンツ変換
第3章 距離と時間と不変間隔
第4章 4元ベクトルとE=mc^2
(登山の部)
第5章 一般座標変換と共変微分
第6章 リーマン曲率テンソルとメトリック
第7章 測地線方程式とエネルギー・運動量テンソル
第8章 アインシュタイン方程式
エピローグ 方程式を「読む」「解く」ということ
これが深川さんの「冒険」の順番であり、本書の構成は次の杉山先生の相対性理論の教科書にならっている。本書ではまた、須藤先生の教科書も参考にされている。(この他、巻末の参考文献が素晴らしい。)
「相対性理論 (講談社基礎物理学シリーズ):杉山直」(Kindle版)
「一般相対論入門 改訂版:須藤靖」(Kindle版)


本書を読めば著者が数年かけて学んできた驚きや感動をを追体験できる。空間が、そして時空が歪むのがどういうことなのかを数式で理解することでよりリアルに実感することができる。T_NAKAさんがお書きになっているように、本書はアインシュタイン方程式を数式で解説している「もっともページ数が少なく、安価な本」なのだ。
しかし、本書を読めばド文系の初学者がアインシュタイン方程式を理解できるというわけではない。あくまでも追体験して概要をつかむことができるレベルまでという限界があるのを承知していただきたい。(それでも感動できるはず。)
初学者は初めて見る専門用語をとかく誤解しがちだ。物理法則の共変性と共変ベクトルでは「共変」の意味が違うし、共変ベクトル・反変ベクトルがあり、共変微分があるのなら反変微分もあるのだろうなどと思ったりもする。本書を読めば、少なくともそのような誤解で無駄な時間を使うことを避けることができる。
テンソルやリーマン幾何学も、数学書で学ぶと挫折しがちだが、本書で概念をつかんでおいてから、他の教科書で詳しく学ぶとよい。また本書で「メトリック」と書かれているのは他の本では「計量」と書かれていることが多い。
アインシュタイン方程式を学ぶとき、初学者が上で紹介した杉山先生や須藤先生の本のような「教科書」で独学するのは無理だと僕は思っている。
というわけで、本書を読み終えて独学で学んでみたいと思うなら「ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平」や「趣味で相対論:広江克彦」(無料で学ぶのであれば「EMANの相対性理論」)のような副読本のほうがよいと思う。そして分厚い本でも大丈夫という方には「一般相対性理論を一歩一歩数式で理解する: 石井俊全」をお勧めする。
ぜひ、チャレンジしていただきたい。
以下は著者による、本書の紹介文である。
【この無謀な願望が、すべてのはじまりだった】
嗚呼、わかりたい。ちょっとでいいから、数式で宇宙がどう書かれているのかをわかってみたい──そう思うのが人情だろう。だって、彼らは自分と同じ人間なのだ。しかも間違いなく、ものすごく面白いことを研究している。ならば、交流したいじゃないか。カタコトでいいから、同じ言葉でお喋りしてみたいじゃないか。それはもう、外国旅行から帰国するやいなや「やっぱり英語できるようになりたい!」と駅前留学しちゃうような気分である。(プロローグより)
【著者の苦闘を見物するうちに相対性理論の真髄が見えてくる】
・数式だからわかる、時間と空間に代わる「不変なもの」
・こうすれば「時間の延び」が計算できる
・E=mc2はどのように導けるのか ・アインシュタインはグニャグニャな空間といかに戦ったか
・時間と空間が「混じる」とはどういうことか ・「行列のお化け」テンソルとは何者か
・ブラックホールの解はいかに導けるか ・ここだけの話、数式は飛ばして文章と絵だけでも楽しめます
関連ページ:
本書の『プロローグ 宇宙が「数学の言葉」で書かれているのなら』『(準備の部)第1章 ガリレオの相対性原理』までは、次のページで読むことができる。
アインシュタイン方程式を読む ド文系が挑む「一般相対性理論」への道
第1回 数式を知らずして、宇宙がわかるものか!
第2回 読み方すらわからない
第3回 これが行列の化け物「テンソル」だ!
第4回 「出発前の準備」が特殊相対性理論
第5回 あんがい簡単だった「ガリレイ変換」の式
第6回 微分は「わかったつもり」になって進もう
関連記事:
一般相対性理論に挑戦しよう!
https://blog.goo.ne.jp/ktonegaw/e/ea7ad9292ce01ad4abbbc8c98f3303d0
趣味で相対論(EMANの物理学):感想
https://blog.goo.ne.jp/ktonegaw/e/5fe7d774a955f3bb9d8270f6113e453f
ブラックホールと時空の方程式:15歳からの一般相対論:小林晋平
https://blog.goo.ne.jp/ktonegaw/e/f4401f2ce79451070b7b9c089f304315
発売情報:一般相対性理論を一歩一歩数式で理解する: 石井俊全
https://blog.goo.ne.jp/ktonegaw/e/1699a1c22477c269c68c02091d0ca049
発売情報: 重力(上)(下) アインシュタインの一般相対性理論入門: ジェームズ・B・ハートル
https://blog.goo.ne.jp/ktonegaw/e/c195a49914a852b1c73049bb7b9743e0
時空の幾何学:特殊および一般相対論の数学的基礎
https://blog.goo.ne.jp/ktonegaw/e/ffc643a688ce45dec7460d107fe1392e




「アインシュタイン方程式を読んだら「宇宙」が見えた:深川峻太郎」(Kindle版)

プロローグ 宇宙が「数学の言葉」で書かれているのなら
- 「タテガキのサイエンス」の役割
- われわれも「数学の言葉」で書かれている
- これは「冒険」である
(準備の部)
第1章 ガリレオの相対性原理
- あちこちに顔を出す「μν」の謎
- 最初の衝撃
- R^μνには巨大な中身があった!
- 「登山前の準備」が特殊相対性理論という現実
- ガリレオの「相対性原理」とは?
- 「ガリレイ変換」の式はあんがい簡単だった
- 異なる慣性系の「F=ma」が同じになるか
- とうとう登場しやがった微分記号
- 「d」がついたら「瞬間的な変化量」のこと
- 力の本質は加速度だった!
第2章 時間の延びとローレンツ変換
- ニュートン力学と電磁波の矛盾
- 16歳のアインシュタインの思考実験
- 物理学は妥協を許さない
- 暴かれたニュートン力学の限界
- ミンコフスキー時空図で時空を深く理解する
- 「同時」は慣性系によって異なる!
- 謎の係数「κ」を求めるのだ
- ローレンツ係数「γ」も求めるぞ
- ああ美しきローレンツ変換
第3章 距離と時間と不変間隔
- 「光速度一定」なら時間は延びて距離は縮む
- 時間や距離に代わる「不変な何か」とは
- 線形代数入門
- 相対性理論に欠かせない概念「不変間隔」
- 偏微分との出会いに目を回す
- 「Σ」で数式をおかたづけ♪
- どこに行くんだこの計算は!?
- そして教科書は真っ黒になった
第4章 4元ベクトルとE=mc^2
- アインシュタインが決めた「オレ様ルール」
- 4次元時空ではベクトルの「変換性」はどうなる
- ミンコフスキー・メトリック
- 「反変ベクトル」と「共変ベクトル」
- 「逆行列」で反変と共変をチェンジ!
- 「固有時間」が常識中の常識だと?
- 4元速度から「4元運動量」を求める
- 線形代数入門パート2
- いざ中学理科の復習からE=mc^2へ
(登山の部)
第5章 一般座標変換と共変微分
- 「特殊」から「一般」へ
- 等価原理はこうしてできた
- 「潮汐力」こそが重力の本質
- アインシュタインも苦しんだ
- 出た、一般座標変換!しかし
- いよいよ「テンソル」とご対面
- スカラーとベクトルとテンソルの関係
- ベクトル場の微分がテンソルにならない
- 「共変微分」のおかげで「接続」できました
第6章 リーマン曲率テンソルとメトリック
- ユークリッド幾何学からリーマン幾何学へ
- リーマン曲率テンソルは添え字が4つ!
- グニャグニャな時空のメトリック
- 接続がクリストッフェル記号になるとき
- リッチ・テンソルと「ビアンキの恒等式」
第7章 測地線方程式とエネルギー・運動量テンソル
- この段階でまさかの「積分入門」
- 「最小作用の原理」のせいで遠回り
- 「オイラー=ラグランジュ方程式」に癒される
- 測地線方程式は3通りもある、らしい
- お次は「ポアソン方程式」だってよ
- 「発散」するのはストレスだけでいい
- 重力場のポアソン方程式と万有引力
- おそるべし、エネルギー・運動量テンソル
- 「完全流体でOK」という朗報
第8章 アインシュタイン方程式
- 頂上までの道のりを再確認する
- 左辺の係数「a」と「b」
- 右辺の係数「κ」
- これまでの成果を次々に使うのだ!
- 最終アタック
エピローグ 方程式を「読む」「解く」ということ
- 敗北感と達成感
- 「内側」から方程式を読む
- 数式の予言が当たったことの驚き
- 一般的な解法は存在しない!
- これがシュヴァルツシルト解だ!
- 天才の偉業に「あたりまえ」などない
あとがき
参考文献
さくいん























なお、私のブログ記事をリンクしていただいてありがとうございました。
コメント公開と返信が遅くなり、失礼しました。(このところずっと激務が続いていて、ブログを開く時間がとれていません。)
ディラック「一般相対性理論 (ちくま学芸文庫)」は、今なら読めますが、最初に読んだときは撃沈しました。
調べたところ2006年5月に初挑戦していたようです。ブログの記事タイトルを書名にしていなかったころの記事です。
天才による美しい入門書
https://blog.goo.ne.jp/ktonegaw/e/4d073f3be235b3aa6d7d5e6ea8f788d9
『アインシュタイン方程式を読んだら「宇宙」が見えた』は、とてもよかったです。Kindle版で読みましたが、週末に紙の本も買っておこうとおもいます。
共変微分の添字を上げるだけだからわざわざ定義する必要もないけど。
英語だと直訳は「絶対微分」だから単に共変添字で書いただけの理由でしょうね。
もともと一般相対論の範囲では共変ベクトルと反変ベクトルは同じものの表現違いに過ぎない。
情報幾何学になると違うけど。
反変微分は共変微分の添字を上げるだけなのですね。