
「第3章:エネルギーの保存」からようやく物理学らしい解説がはじまる。
この世界を作っているすべてのモノやコトについて研究するのが物理学だ。モノとは目に見える物質や光、目に見えない電磁波や圧力、温度、熱そして空間や時間も含まれる。コトとは速度や加速度などの運動のほか物体に力を作用させるなどのことである。この意味ではエネルギーはモノに分類されるのかもしれない。またそれらのモノやコトがどのような数量関係でつながっているかを調べるのも物理学である。
けれども勉強を進めていくうちに不思議な状況になる。はじめのうちモノだと思っていたものが実はコトであったり、コトであると思っていたものがモノであったり両者の境界があいまいになってくるのだ。そしてコトとして確かに存在すると考えていたものが本当に存在するのか怪しくなってくる。粒のように考えていた電子が実は波動であったり、せっかく電磁波の一種だとわかった光が光子という粒であったりする。まっすぐだと思われていた空間は重力で曲がり、時間の進み方も遅れてしまう。本質を追求すればするほど不確実な世界が露呈してくるのである。
エネルギーとはこうしたモノの中でいちばん不思議な存在なのだと思う。それは直接見たり触ったり重さを計ったりすることができず、さまざまに形を変えてあちこちに移動する。運動エネルギー、位置エネルギー、熱エネルギー、電磁波のエネルギー、核エネルギーなどである。こういった不思議な量がそれぞれお互いに計算でき、その総量は変化しないというのが「エネルギーの保存」と呼ばれている法則だ。
このようにその存在がわかりにくいエネルギーというモノが物理学のいちばん基本的な量として考えられているのだ。そしてこれが特殊相対論から導かれる E=mc^2 という方程式で質量 - その存在が確からしいモノと等価である、つまりエネルギーと質量は変換できるということがわかったのだ。
自然の法則や理論というものはできる限り正確で確からしい物を基本にして組み立てていくと、その在り様がすべて正確に求められるのだろう。だから人間は原子を考え、エネルギーを考え自然法則の出発点となる基本量や基本的な粒子を追い求めてきた。1つか2つでも確かなものがなければ全体があやうくなってしまうからだ。
とりあえずエネルギーというひとつの手がかりを前提にしてこの本の残りの章は「力学」をテーマにして進むわけである。
ところでファインマン先生はこの章で「位置エネルギー」から紹介している。位置エネルギーにも「重力による位置エネルギー」のほか「電気力による位置エネルギー」、「磁力による位置エネルギー」など「力」の種類に応じた位置エネルギーというものがあることを忘れてはいけない。
先日「力学は本当に簡単か?(球の衝突実験)」の記事で紹介したガウス加速器は「磁力による位置エネルギー」を運動エネルギーに変換して見せた例である。だから「磁力のエネルギー」という言い方は正しくない。運動エネルギーへの変換によって磁力が減るわけではないわけである。重力についても同様で「重力エネルギー」という言い方は正確ではない。
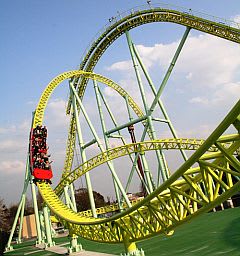
[運動エネルギー]+[重力による位置エネルギー]=一定
という力学的エネルギー保存則が成り立つので、摩擦や空気抵抗がゼロという理想的な条件の下で次のようなジェットコースターでは地上からの高さが同じ位置での乗り物のスピードは必ず等しくなるわけだ。たとえ軌道がどんなに複雑にカーブしていても、そして宙返りしていてもそれは成り立っている。
-----------------
「第4章:時間と距離」では物理学が扱う時間や距離(空間)がどのような範囲のものであるか、そしてそれらをどのように正確に測るかということを解説している。モノやコトが時間や空間の中に存在するために、その「入れ物」について正しく知っておこうというわけだ。
数学では無限大や無限小を考えることによって興味深い理論が導かれるのであるが、それはあくまで仮想世界でのこと。物理学でどこまで大きな時間や空間、どこまで小さい時間や空間を取り扱えるのだろうか?そしてその極限の世界では物事は普段私たちが目にしている世界と同じ法則に支配された世界が広がっているのであるか?
時間についていえば原子核の直径を光が通過するのにかかる時間のような小さい時間から宇宙の年齢のような大きな時間までを取り扱うのである。量子力学ではプランク時間という更に小さい時間もでてくる。距離についていえば原子核の中を構成する素粒子のような小さな長さから「宇宙の果て」までを取り扱う。
次の写真は今年の4月に多数の望遠鏡を使って観測された天体で「ヒミコ」と名づけられた。その質量はなんと銀河系の10倍もあるそうで、地球から129億光年の距離にある。大きさは5.5万光年だそうだ。(詳細な説明はこちらのページを参照)このように巨大なものがひとつの天体としてどうして爆発もせず、つぶれもせずに存在できるのか、その理由はまだ解明されていない。
巨大天体ヒミコ(合成写真)

スケールが大きいだけで話は単純なのだが、私たちがそのような小さいスケールから大きなスケールの世界のごく一部しか知覚できないことを忘れてはならない。それ以外の一部分については観測機器を使って間接的に見ることができるが、さらにそれでも見ることのできないほとんどの部分は理論的に予想されているに過ぎないことを忘れてはならない。それが本当に存在するかどうかは数式によって知るというのが理論物理学である。
もちろん理論だけで物理学が完結するということはない。実験の重要性はこの章の最後で示されている「原子核の直径を求める」計算方法でもよくわかる。厚さ1cmの炭素ブロックに高エネルギーの粒子線をあてて、炭素ブロックを通過する粒子の割合を実験すれば、それを元にして簡単な数式で原子核の半径を計算することができるのだ。
それによると原子核の半径は10のマイナス15メートルということになり、別の方法で計算された炭素原子の半径が10のマイナス10メートルという値とくらべると、原子核は原子の中の10万分の1の大きさを占めているにすぎない。現在利用可能な最高性能の顕微鏡で見えるのはせいぜい金属の原子の大きさまでである。
参考写真:
金の原子の写真(金箔の表面):もちろん金の原子に色はない。後から人為的に着色したものである。

水素原子の写真

炭素原子の写真:ダイヤモンドの結晶

炭素原子の立体写真(ステレオグラム):人為的に着色したもので実際には色はない。

この記事が気に入った方は下のボタンをひとつづつクリックしてくださいね!このブログのランキブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。
「ファインマン物理学」のレビューを参照したい方、購入したい方はそれぞれ画像をクリックしてください。





























数学をかなり勉強していないと現代の物理学は私には理解できません。難しいですね。
このファインマン物理学の第1巻、第2巻を読むには少なくとも高校の数IIIレベルの学習経験が必要だと思います。また第3巻~第5巻は大学教養課程の物理数学を理解している必要があると思います。以前記事で紹介した「よくわかる物理数学の基本と仕組み」という本がお勧めです。
近頃は高校数学についても受験数学にとらわれず、「理解する」ということに重点を置いた良書が出ていますので、以前よりだいぶ社会人が数学を勉強しなおしやすい環境になっていると思いました。
かずおさんのこれまでの学習経験がわかりませんので、もしかしたら見当ハズレの返信になってしまっていたらごめんなさい。
ちなみに僕は大学で数学を専攻していました。優秀ではなくどうにか授業についていけていたという感じです。学生の頃、物理学はほとんど勉強していませんでした。