
「天秤の魔術師 アルキメデスの数学:林栄治、斎藤憲」(正誤表)
内容紹介:
アルキメデスは古代世界で最も有名な数学者であり、技術者でもあった。しかしその数学の内容を説明することは、それほど容易ではない。そこで本書では、『方法』というそれほど大きくない著作を中心に展開し、アルキメデスの議論の背景や意図を徹底的に探求して解説することを目指した。この『方法』という著作は、理論的(あるいは仮想的)な天秤の使用によって驚くような結果を導き出す、非常に魅力的な技法を含む―本書のタイトルの「天秤の魔術師」がここから来ることは言うまでもない。しかも幾何学と機械学の二つの分野にまたがるアルキメデスの数学的活動をいわば要約する著作であり、アルキメデスの数学のかなりの部分を把握することができる。読者は、アルキメデスが問題解決の技法を発見し、それを利用し、さらに他の問題を解くために変形・発展させていく場面に立ち会える。『方法』を伝える唯一の写本の最新の解読成果も利用しつつ、数学史の書物では例を見ないほどに証明や議論の展開を丁寧に解説した本書は、数学教育の教材としても十分な意義をもつだろう。アルキメデスの数学の世界を堪能してほしい。
2009年12月23日刊行、268ページ。
著者について:
林栄治
1971年早稲田大学教育学部理学科数学専修課程卒業。1972年より、都立工芸高校、群馬県太田市立商業高校、群馬県立桐生女子高校、高崎工業高校に勤務。1999年早稲田大学大学院教育学研究科数学教育専攻修了。2007年高崎工業高校教諭退職。在職中に、三省堂高校数学教科書執筆グループに参加。『数学セミナー』、『数学教室』、『数学教育』などに研究成果を発表。とくに、1985年11月『数学セミナー』のアルキメデスの求積に関する研究の発表が以後の研究の端緒となり、1993、4年『科学史研究』にアルキメデス『方法』に関する論文発表、現在に至る。
斎藤憲
HP: https://www.greekmath.org/kensaito/index_j.html
Twitter: @ken_saito_greek
1958年生まれ。1980年東京大学教養学部卒業(科学史科学哲学)。1982年東京大学文学部卒業(イタリア語イタリア文学)。1990年東京大学大学院理学系研究科博士課程(科学史科学基礎論)修了。理学博士。千葉大学文学部助教授、大阪府立大学総合科学部助教授、人間社会学部助教授・准教授を経て、2011年より同大学人間社会学部教授。専攻はギリシア数学史。
理数系書籍のレビュー記事は本書で449冊目。
10月に読んだ「解読! アルキメデス写本: リヴィエル・ネッツ、ウィリアム・ノエル」という科学教養書で、古代ギリシアの数学者アルキメデスの偉業を思い知った。これは2000年以上前にアルキメデスがパピルスの巻物に書き残した数学研究の内容が、数奇な運命を経て現代の科学技術によって、解読しなおされた経緯を紹介した本だ。
アルキメデスの著作は、その後羊皮紙に書かれた本として書き写され、現在はそれぞれA写本、B写本、C写本と呼ばれている。「解読! アルキメデス写本」はこのうち、C写本について紹介した本で、主に彼が発見した「求積法」について書かれている。つまり図形や立体の面積、体積を求める方法、そしてその証明を紹介した著作である。C写本に含まれる求積法の部分にアルキメデスは「方法」という名前をつけていた。
『砂粒を数える者』(A写本)
『平面のつり合いについて』(A写本、B写本、C写本)
『放物線の求積について』(A写本、B写本)
『球と円柱について』(A写本、C写本)
『円柱の計測』(A写本、C写本)
『螺旋について』(A写本、C写本)
『円錐状体と球状体について』(A写本)
『浮体について』(B写本、C写本)
『方法』(C写本)
『ストマキオン』 (C写本)
しかし、「解読! アルキメデス写本」には具体的に数学的な解説もされているものの、あくまで紹介程度のもので詳しいことを知ることができない。もう少し詳しく知りたいと思い、「天秤の魔術師 アルキメデスの数学:林栄治、斎藤憲」を読むことにしたわけだ。
円錐や球、円柱の体積を求める公式は小学校の算数で学ぶ。そしてそれらの公式を積分を使って求めることは、高校の数学IIIまでの数学で理解することができる。けれども積分法が発明されるはるか以前、アルキメデスはどのようにしてこれらの体積を求めたのだろうか?そして半径が同じ場合、円錐、球、円柱の体積比は1:2:3であることが知られている。(参考:「中学1年の数学の証明なしの解説ページ」)
これは円錐、球、円柱の体積比が1:2:3であることを確認する実験動画だ。
小学生のとき僕は三角錐の体積についても、底面積と高さが同じ三角柱の体積の3分の1であることを知って、とても驚いたことがある。底面が円のときと三角形のときの体積は、まるで違う形の公式になると思っていたからだ。それならば四角柱、五角柱、六角柱、...N角柱であってもそれらの錐の体積は3分の1になるはずだ。小学生のときはそこまで想像をめぐらせて終わっていた。そして、球の体積が円柱や円錐の体積と整数比になることなどは、僕の理解をはるかに超えていた。
ちなみに、三角形の面積の公式に2分の1が掛けられているのは、平面が縦横の2次元であることの現れであり、三角錐や円錐の体積の公式に3分の1が掛けられているのは立体が縦横高さの3次元であることの現れである。
アルキメデスは球の体積を求めるために、仮想天秤という方法を考案した。小学校で習うように天秤はつり合いの中心からの距離が遠くなるほど、それに反比例した質量の物体をつるせばつり合わせることができる。彼は円柱と円錐、球を天秤に吊るしてつり合わせた状態を想像して、切断面の質量についてつり合いの中心からの距離の比を求め、切断面の荷重分布に従いその総和をとることで、釣り合う物体と球との質量比(=体積比)を求めていたのだ。想像上の天秤とはいえ、実際の道具を使った求積法だから、アルキメデスおよび本書ではこれを「機械学による方法」と呼んでいる。重要な点は、アルキメデスは実験をして立体をつり合わせて体積を求めたのではない。あくまで仮想天秤という思考実験をしただけなのだ。
これは、仮想天秤を使って球の体積を求める方法を解説した動画である。文字による説明は、積分を使わずにアルキメデスの幾何学的方法を現代の表記でおこなっていることに注意していただきたい。
なんと斬新な発想だろうか。何もない状況から、自分はこの方法を思いつくことができるだろうか?もちろんできないと思う。さらに彼は、同じ方法を使って半球の重心の位置を求める方法を紹介している。
アルキメデスが天才数学者と言われるゆえんは、これだけにとどまっていないことだ。仮想天秤という機械学を使った方法で体積や重心を求めた後、天秤に吊るしたこれらの図形についてつり合いの中心からの距離などの比を用いた方法で、「幾何学的な証明」をしていることだ。さらに、アルキメデスは現在の積分法に通じる「取り崩し法」という手法を発明し、立体を無限分割したそれぞれの体積の総和として立体全体の体積を求めることまで行っている。曲線の下の面積を求めるために長方形公式を使って計算することを立体に応用した手法である。この段階で、アルキメデスは1900年後にニュートンやライプニッツが発明する積分法、そして無限級数の計算をすることによって20世紀にカントールによって導かれた実無限の概念にまで達していたことがわかるのだ。まさに驚異的である。
数学者無限をど䛾ように捉えてきたか
https://www.ms.u-tokyo.ac.jp/~kohno/lectures/kohno_infinity.pdf
ガリレイ、ニュートン、ライプニッツらは、ラテン語に翻訳されたアルキメデスのこの著作を読んでいた。この『方法』に書かれていた求積法を参考にして微積分法を考案し、これが1687年に刊行されたニュートンの『プリンキピア(自然哲学の数学的方法)』、近代科学の誕生に結び付いたと言ってよい。
本書の章立ては次のとおりだ。
第1章 アルキメデスとその著作
第2章 回転放物体の切片(命題4, 5)
第3章 球(回転楕円体)の体積と半球の重心(命題2, 3, 6)
第4章 球の切片(命題7-10)
第5章 残された立体:回転双曲体命題11の復元
第6章 放物線の切片の面積(命題1)
第7章 爪形の体積(命題12+13:天秤による求積)
第8章 爪形の2つの求積法(命題14, 15)
第9章 交差円柱とアルキメデスの意図
第10章 交差円柱:失われた証明
第11章 補章
球だけでなく回転放物体、回転双曲体、爪型(斜切円柱)、交差円柱などさまざまな立体の体積を求めていることがおわかりだろう。本書ではアルキメデスの仮想天秤の方法、幾何学による証明だけでなく、それぞれについて現代の積分法に匹敵する取り崩し法のよる計算方法も紹介している。
彼がどのような立体を仮想天秤に吊るして求積を行ったか、著者は実際に写真に撮って紹介している。このような状況を私たちはモデル化して計算することができるだろうか?この段階でアルキメデスの本領が発揮される。これらの立体の体積を求めるためには、立体と立体が空間の同じ領域で重なり合うようにして仮想天秤にかけなければならないケースがでてくる。ここに紹介する写真は、立体と立体が重なり合わない状況を示したものにすぎない。重なり合う状況について、本書では図示して解説している。
回転放物体の体積を求める

回転放物体の体積を求める
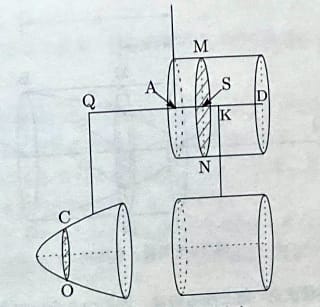
円柱、円錐、球のつり合い

爪型(斜切円柱)の体積や重心を求める:拡大

参考:体積・表面積の数学公式集
さて、僕にとっての本書の難易度であるが、じっくり読んだところ証明を含めてやっと理解できる程度だった。もちろん、自分で本書で紹介されているような仮想天秤に立体を吊るすモデルは思いつくことができないし、自分で証明することもできないと思う。証明を理解できたとき、何かすごいことを経験してしまった感動が湧いてくる。
このような立体の体積や重心を求めることが、いったい何の役に立つのだろうか?単なる数学的な意義にとどまるのだろうか?それは本書の最後のほうで解説されているように、建築物の設計に利用できるのである。古代ギリシア建築は曲面を多用し、とても美しい。神殿などの巨大建築を構成するパーツはその優雅さだけでなく、バランスよく組み合わせるために体積や重心の位置を求めておく必要がある。つまり、アルキメデスによる求積法は応用数学でもあったのだ。
そして円錐形は物理学にも現れることがある。特殊相対論・弦理論では「オービフォールド」と呼ばれるクリスマス・パーティーでかぶるとんがり帽子のような形に巻かれた形の余剰次元の空間として存在している。これは「初級講座弦理論 基礎編:B.ツヴィーバッハ」の第2章「特殊相対性理論・光錐座標系・余剰次元」で解説されている。
本書はお二人の先生による共著である。そのうちのお一人の斎藤先生は、その後2014年に次の本をお書きになっている。今回紹介した本より手ごろな分量で、Kindle版としても刊行されている。
「アルキメデス『方法』の謎を解く:斎藤憲」(Kindle版)(正誤表)

そして、ここまでの2冊の元にされたのが次の本だ。この本は1990年に刊行され、アルキメデスの『方法』の全訳とその解説がされている。刊行年からおわかりのように1998年以降に現代の科学技術により再発見された内容は含まれていないことに注意すべきだ。この本は、1906年にハイベアにより解読された内容をベースにしている。
「アルキメデス方法:佐藤徹」

2200年前の数学に想いを巡らせていただきたい。本書に書かれていることは、すべてこの写本に収められていたのだ。
ウィリアム・ノエル:失われたアルキメデスの写本の解読(日本語字幕あり)
関連記事:
解読! アルキメデス写本: リヴィエル・ネッツ、ウィリアム・ノエル
https://blog.goo.ne.jp/ktonegaw/e/aba2a2674ac2cb8c79ead88f65a2eb6e
メルマガを書いています。(目次一覧)





「天秤の魔術師 アルキメデスの数学:林栄治、斎藤憲」(正誤表)

第1章 アルキメデスとその著作
1.1 アルキメデスの2つの顔と著作『方法』
1.2 アルキメデスの時代と逸話
1.3 著作を伝える写本
1.4 甦ったC写本と『方法』
1.5 数学的予備知識:本書で使われる定理
第2章 回転放物体の切片(命題4, 5)
2.1 『方法』の構成と内容
2.2 回転放物体の切片の体積(命題4)
2.3 回転放物体の切片の重心位置(命題5)
2.4 回転放物体の重心位置に関する補足
第3章 球(回転楕円体)の体積と半球の重心(命題2, 3, 6)
3.1 球の体積(命題2)
3.2 回転楕円体の体積(命題3)
3.3 半球の重心位置(命題6)
3.4 半球の重心位置に関する補足
第4章 球の切片(命題7-10)
4.1 球の切片の体積(命題7)
4.2 回転楕円体の切片(命題8)
4.3 球の切片の重心位置(命題9)
4.4 回転楕円体の切片の重心位置(命題10)
第5章 残された立体:回転双曲体命題11の復元
5.1 回転双曲体の切片の体積
5.2 証明の復元(回転双曲体の切片の体積)
5.3 回転双曲体の切片の重心位置
5.4 証明の復元(回転双曲体の切片の重心位置)
第6章 放物線の切片の面積(命題1)
6.1 放物線の切片と『方法』の命題の順序
6.2 『方法』命題1:放物線の切片の面積
6.3 放物線の切片:同じ結果に3つの議論
6.4 『放物線の求積』(1):天秤を使った求積
6.5 『放物線の求積』(2):後半の幾何学的証明
6.6 アルキメデスの発見と証明:著作の執筆順序
6.7 新たな謎:『方法』の末尾とアルキメデスの意図
第7章 爪形の体積(命題12+13:天秤による求積)
7.1 命題の概要
7.2 アルキメデスの議論
7.3 見落とされた球との関連
第8章 爪形の2つの求積法(命題14, 15)
8.1 命題14の概要
8.2 アルキメデスの議論
8.3 命題14をどう評価するか
8.4 参考:命題15(二重帰謬法による爪形の求積)
第9章 交差円柱とアルキメデスの意図
9.1 残された図形:交差円柱
9.2 球・爪形・交差円柱の共通性
第10章 交差円柱:失われた証明
10.1 『方法』の羊皮紙の構成
10.2 方法の末尾部分の謎
10.3 残された可能性:爪形との比較
10.4 アルキメデスの意図をさぐる
10.5 浴場の丸屋根と交差円柱
第11章 補章
11.1 『平面のつり合いについて』と失われた著作
11.2 天秤を使った爪形の求積
11.3 アルキメデスの時代の円錐曲線とその回転体の名称
11.4 『方法』命題4:原文の全訳
参考文献
内容紹介:
アルキメデスは古代世界で最も有名な数学者であり、技術者でもあった。しかしその数学の内容を説明することは、それほど容易ではない。そこで本書では、『方法』というそれほど大きくない著作を中心に展開し、アルキメデスの議論の背景や意図を徹底的に探求して解説することを目指した。この『方法』という著作は、理論的(あるいは仮想的)な天秤の使用によって驚くような結果を導き出す、非常に魅力的な技法を含む―本書のタイトルの「天秤の魔術師」がここから来ることは言うまでもない。しかも幾何学と機械学の二つの分野にまたがるアルキメデスの数学的活動をいわば要約する著作であり、アルキメデスの数学のかなりの部分を把握することができる。読者は、アルキメデスが問題解決の技法を発見し、それを利用し、さらに他の問題を解くために変形・発展させていく場面に立ち会える。『方法』を伝える唯一の写本の最新の解読成果も利用しつつ、数学史の書物では例を見ないほどに証明や議論の展開を丁寧に解説した本書は、数学教育の教材としても十分な意義をもつだろう。アルキメデスの数学の世界を堪能してほしい。
2009年12月23日刊行、268ページ。
著者について:
林栄治
1971年早稲田大学教育学部理学科数学専修課程卒業。1972年より、都立工芸高校、群馬県太田市立商業高校、群馬県立桐生女子高校、高崎工業高校に勤務。1999年早稲田大学大学院教育学研究科数学教育専攻修了。2007年高崎工業高校教諭退職。在職中に、三省堂高校数学教科書執筆グループに参加。『数学セミナー』、『数学教室』、『数学教育』などに研究成果を発表。とくに、1985年11月『数学セミナー』のアルキメデスの求積に関する研究の発表が以後の研究の端緒となり、1993、4年『科学史研究』にアルキメデス『方法』に関する論文発表、現在に至る。
斎藤憲
HP: https://www.greekmath.org/kensaito/index_j.html
Twitter: @ken_saito_greek
1958年生まれ。1980年東京大学教養学部卒業(科学史科学哲学)。1982年東京大学文学部卒業(イタリア語イタリア文学)。1990年東京大学大学院理学系研究科博士課程(科学史科学基礎論)修了。理学博士。千葉大学文学部助教授、大阪府立大学総合科学部助教授、人間社会学部助教授・准教授を経て、2011年より同大学人間社会学部教授。専攻はギリシア数学史。
理数系書籍のレビュー記事は本書で449冊目。
10月に読んだ「解読! アルキメデス写本: リヴィエル・ネッツ、ウィリアム・ノエル」という科学教養書で、古代ギリシアの数学者アルキメデスの偉業を思い知った。これは2000年以上前にアルキメデスがパピルスの巻物に書き残した数学研究の内容が、数奇な運命を経て現代の科学技術によって、解読しなおされた経緯を紹介した本だ。
アルキメデスの著作は、その後羊皮紙に書かれた本として書き写され、現在はそれぞれA写本、B写本、C写本と呼ばれている。「解読! アルキメデス写本」はこのうち、C写本について紹介した本で、主に彼が発見した「求積法」について書かれている。つまり図形や立体の面積、体積を求める方法、そしてその証明を紹介した著作である。C写本に含まれる求積法の部分にアルキメデスは「方法」という名前をつけていた。
『砂粒を数える者』(A写本)
『平面のつり合いについて』(A写本、B写本、C写本)
『放物線の求積について』(A写本、B写本)
『球と円柱について』(A写本、C写本)
『円柱の計測』(A写本、C写本)
『螺旋について』(A写本、C写本)
『円錐状体と球状体について』(A写本)
『浮体について』(B写本、C写本)
『方法』(C写本)
『ストマキオン』 (C写本)
しかし、「解読! アルキメデス写本」には具体的に数学的な解説もされているものの、あくまで紹介程度のもので詳しいことを知ることができない。もう少し詳しく知りたいと思い、「天秤の魔術師 アルキメデスの数学:林栄治、斎藤憲」を読むことにしたわけだ。
円錐や球、円柱の体積を求める公式は小学校の算数で学ぶ。そしてそれらの公式を積分を使って求めることは、高校の数学IIIまでの数学で理解することができる。けれども積分法が発明されるはるか以前、アルキメデスはどのようにしてこれらの体積を求めたのだろうか?そして半径が同じ場合、円錐、球、円柱の体積比は1:2:3であることが知られている。(参考:「中学1年の数学の証明なしの解説ページ」)
これは円錐、球、円柱の体積比が1:2:3であることを確認する実験動画だ。
小学生のとき僕は三角錐の体積についても、底面積と高さが同じ三角柱の体積の3分の1であることを知って、とても驚いたことがある。底面が円のときと三角形のときの体積は、まるで違う形の公式になると思っていたからだ。それならば四角柱、五角柱、六角柱、...N角柱であってもそれらの錐の体積は3分の1になるはずだ。小学生のときはそこまで想像をめぐらせて終わっていた。そして、球の体積が円柱や円錐の体積と整数比になることなどは、僕の理解をはるかに超えていた。
ちなみに、三角形の面積の公式に2分の1が掛けられているのは、平面が縦横の2次元であることの現れであり、三角錐や円錐の体積の公式に3分の1が掛けられているのは立体が縦横高さの3次元であることの現れである。
アルキメデスは球の体積を求めるために、仮想天秤という方法を考案した。小学校で習うように天秤はつり合いの中心からの距離が遠くなるほど、それに反比例した質量の物体をつるせばつり合わせることができる。彼は円柱と円錐、球を天秤に吊るしてつり合わせた状態を想像して、切断面の質量についてつり合いの中心からの距離の比を求め、切断面の荷重分布に従いその総和をとることで、釣り合う物体と球との質量比(=体積比)を求めていたのだ。想像上の天秤とはいえ、実際の道具を使った求積法だから、アルキメデスおよび本書ではこれを「機械学による方法」と呼んでいる。重要な点は、アルキメデスは実験をして立体をつり合わせて体積を求めたのではない。あくまで仮想天秤という思考実験をしただけなのだ。
これは、仮想天秤を使って球の体積を求める方法を解説した動画である。文字による説明は、積分を使わずにアルキメデスの幾何学的方法を現代の表記でおこなっていることに注意していただきたい。
なんと斬新な発想だろうか。何もない状況から、自分はこの方法を思いつくことができるだろうか?もちろんできないと思う。さらに彼は、同じ方法を使って半球の重心の位置を求める方法を紹介している。
アルキメデスが天才数学者と言われるゆえんは、これだけにとどまっていないことだ。仮想天秤という機械学を使った方法で体積や重心を求めた後、天秤に吊るしたこれらの図形についてつり合いの中心からの距離などの比を用いた方法で、「幾何学的な証明」をしていることだ。さらに、アルキメデスは現在の積分法に通じる「取り崩し法」という手法を発明し、立体を無限分割したそれぞれの体積の総和として立体全体の体積を求めることまで行っている。曲線の下の面積を求めるために長方形公式を使って計算することを立体に応用した手法である。この段階で、アルキメデスは1900年後にニュートンやライプニッツが発明する積分法、そして無限級数の計算をすることによって20世紀にカントールによって導かれた実無限の概念にまで達していたことがわかるのだ。まさに驚異的である。
数学者無限をど䛾ように捉えてきたか
https://www.ms.u-tokyo.ac.jp/~kohno/lectures/kohno_infinity.pdf
ガリレイ、ニュートン、ライプニッツらは、ラテン語に翻訳されたアルキメデスのこの著作を読んでいた。この『方法』に書かれていた求積法を参考にして微積分法を考案し、これが1687年に刊行されたニュートンの『プリンキピア(自然哲学の数学的方法)』、近代科学の誕生に結び付いたと言ってよい。
本書の章立ては次のとおりだ。
第1章 アルキメデスとその著作
第2章 回転放物体の切片(命題4, 5)
第3章 球(回転楕円体)の体積と半球の重心(命題2, 3, 6)
第4章 球の切片(命題7-10)
第5章 残された立体:回転双曲体命題11の復元
第6章 放物線の切片の面積(命題1)
第7章 爪形の体積(命題12+13:天秤による求積)
第8章 爪形の2つの求積法(命題14, 15)
第9章 交差円柱とアルキメデスの意図
第10章 交差円柱:失われた証明
第11章 補章
球だけでなく回転放物体、回転双曲体、爪型(斜切円柱)、交差円柱などさまざまな立体の体積を求めていることがおわかりだろう。本書ではアルキメデスの仮想天秤の方法、幾何学による証明だけでなく、それぞれについて現代の積分法に匹敵する取り崩し法のよる計算方法も紹介している。
彼がどのような立体を仮想天秤に吊るして求積を行ったか、著者は実際に写真に撮って紹介している。このような状況を私たちはモデル化して計算することができるだろうか?この段階でアルキメデスの本領が発揮される。これらの立体の体積を求めるためには、立体と立体が空間の同じ領域で重なり合うようにして仮想天秤にかけなければならないケースがでてくる。ここに紹介する写真は、立体と立体が重なり合わない状況を示したものにすぎない。重なり合う状況について、本書では図示して解説している。
回転放物体の体積を求める

回転放物体の体積を求める

円柱、円錐、球のつり合い

爪型(斜切円柱)の体積や重心を求める:拡大

参考:体積・表面積の数学公式集
さて、僕にとっての本書の難易度であるが、じっくり読んだところ証明を含めてやっと理解できる程度だった。もちろん、自分で本書で紹介されているような仮想天秤に立体を吊るすモデルは思いつくことができないし、自分で証明することもできないと思う。証明を理解できたとき、何かすごいことを経験してしまった感動が湧いてくる。
このような立体の体積や重心を求めることが、いったい何の役に立つのだろうか?単なる数学的な意義にとどまるのだろうか?それは本書の最後のほうで解説されているように、建築物の設計に利用できるのである。古代ギリシア建築は曲面を多用し、とても美しい。神殿などの巨大建築を構成するパーツはその優雅さだけでなく、バランスよく組み合わせるために体積や重心の位置を求めておく必要がある。つまり、アルキメデスによる求積法は応用数学でもあったのだ。
そして円錐形は物理学にも現れることがある。特殊相対論・弦理論では「オービフォールド」と呼ばれるクリスマス・パーティーでかぶるとんがり帽子のような形に巻かれた形の余剰次元の空間として存在している。これは「初級講座弦理論 基礎編:B.ツヴィーバッハ」の第2章「特殊相対性理論・光錐座標系・余剰次元」で解説されている。
本書はお二人の先生による共著である。そのうちのお一人の斎藤先生は、その後2014年に次の本をお書きになっている。今回紹介した本より手ごろな分量で、Kindle版としても刊行されている。
「アルキメデス『方法』の謎を解く:斎藤憲」(Kindle版)(正誤表)

そして、ここまでの2冊の元にされたのが次の本だ。この本は1990年に刊行され、アルキメデスの『方法』の全訳とその解説がされている。刊行年からおわかりのように1998年以降に現代の科学技術により再発見された内容は含まれていないことに注意すべきだ。この本は、1906年にハイベアにより解読された内容をベースにしている。
「アルキメデス方法:佐藤徹」

2200年前の数学に想いを巡らせていただきたい。本書に書かれていることは、すべてこの写本に収められていたのだ。
ウィリアム・ノエル:失われたアルキメデスの写本の解読(日本語字幕あり)
関連記事:
解読! アルキメデス写本: リヴィエル・ネッツ、ウィリアム・ノエル
https://blog.goo.ne.jp/ktonegaw/e/aba2a2674ac2cb8c79ead88f65a2eb6e
メルマガを書いています。(目次一覧)





「天秤の魔術師 アルキメデスの数学:林栄治、斎藤憲」(正誤表)

第1章 アルキメデスとその著作
1.1 アルキメデスの2つの顔と著作『方法』
1.2 アルキメデスの時代と逸話
1.3 著作を伝える写本
1.4 甦ったC写本と『方法』
1.5 数学的予備知識:本書で使われる定理
第2章 回転放物体の切片(命題4, 5)
2.1 『方法』の構成と内容
2.2 回転放物体の切片の体積(命題4)
2.3 回転放物体の切片の重心位置(命題5)
2.4 回転放物体の重心位置に関する補足
第3章 球(回転楕円体)の体積と半球の重心(命題2, 3, 6)
3.1 球の体積(命題2)
3.2 回転楕円体の体積(命題3)
3.3 半球の重心位置(命題6)
3.4 半球の重心位置に関する補足
第4章 球の切片(命題7-10)
4.1 球の切片の体積(命題7)
4.2 回転楕円体の切片(命題8)
4.3 球の切片の重心位置(命題9)
4.4 回転楕円体の切片の重心位置(命題10)
第5章 残された立体:回転双曲体命題11の復元
5.1 回転双曲体の切片の体積
5.2 証明の復元(回転双曲体の切片の体積)
5.3 回転双曲体の切片の重心位置
5.4 証明の復元(回転双曲体の切片の重心位置)
第6章 放物線の切片の面積(命題1)
6.1 放物線の切片と『方法』の命題の順序
6.2 『方法』命題1:放物線の切片の面積
6.3 放物線の切片:同じ結果に3つの議論
6.4 『放物線の求積』(1):天秤を使った求積
6.5 『放物線の求積』(2):後半の幾何学的証明
6.6 アルキメデスの発見と証明:著作の執筆順序
6.7 新たな謎:『方法』の末尾とアルキメデスの意図
第7章 爪形の体積(命題12+13:天秤による求積)
7.1 命題の概要
7.2 アルキメデスの議論
7.3 見落とされた球との関連
第8章 爪形の2つの求積法(命題14, 15)
8.1 命題14の概要
8.2 アルキメデスの議論
8.3 命題14をどう評価するか
8.4 参考:命題15(二重帰謬法による爪形の求積)
第9章 交差円柱とアルキメデスの意図
9.1 残された図形:交差円柱
9.2 球・爪形・交差円柱の共通性
第10章 交差円柱:失われた証明
10.1 『方法』の羊皮紙の構成
10.2 方法の末尾部分の謎
10.3 残された可能性:爪形との比較
10.4 アルキメデスの意図をさぐる
10.5 浴場の丸屋根と交差円柱
第11章 補章
11.1 『平面のつり合いについて』と失われた著作
11.2 天秤を使った爪形の求積
11.3 アルキメデスの時代の円錐曲線とその回転体の名称
11.4 『方法』命題4:原文の全訳
参考文献






















