
「開立はん」に421,875を置いたところ
[English]
今回から算盤での開立の手順を解説する。開平より複雑さが増し、ずっと面白くなる。
今回は3根法で根が2桁、初根が4以上の場合だ。理論編も参考にしていただきたい。
開立(立方根):3根法(3倍根法、3商法)、定数法、3a^2法、三除九九、三分九九法、三分九九法別法、乗減法(変商法)、3根^2法、折衷法、過大数開立、省略開立など
算盤による421,875の3乗根の解法(答は75)
第1群の数とは立方根を求める数を3桁ずつ区切り、いちばん大きい(いちばん左)の3桁のことである。群の数が根の桁数となる。
421,875 -> (421|875): 421が第1群の数、根の桁数は2。

手順1:421875を置く。第1群は421。

手順2:421以下の立方数は343=7^3。7を初根としてDに立てる。

手順3:421-343=078をGHIに置く。(-a^3)

手順4:3倍根(3×初根)、3x7=21をABに置く。

手順5:3倍根=21でH以降を初根の次4桁目(定位置)に商が立つまで割る。(÷3a)
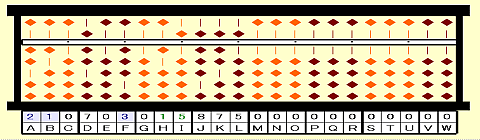
手順6:78÷21=3余り15。商3をFに置き、余り15をHIに置く。

手順7:158を21で割る。

手順8:158÷21=7余り11。商7をGに置き、余り011をHIJに置く。
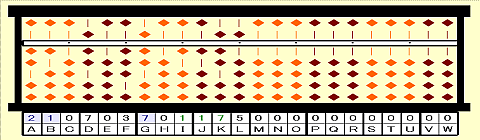
手順9:117を21で割る。

手順10:117÷21=5余り12。商5をHに置き、余り012をIJKに置く。

手順11:37を既根(初根)7で割る。(÷a)
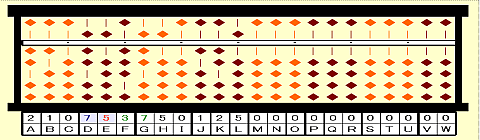
手順12:商5を立て、これを次根とし、Eに置く。
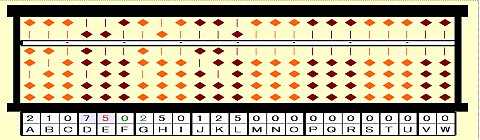
手順13:37-初根x商=37-7x5=02をFGに置く。(-ab)
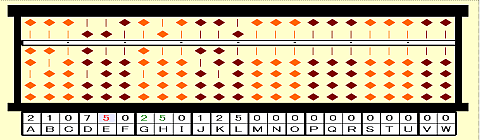
手順14:GHの25に注目する。
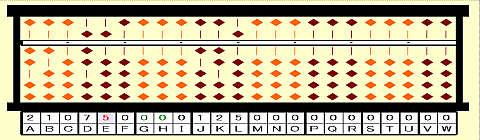
手順15:25-次根^2=25-5^2=00をGHに置く。(-b^2)

手順16:JKLの125に注目する。
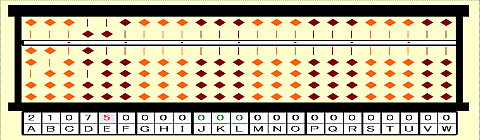
手順17:125-次根^3=125-5^3=000をJKLに置く。(-b^3)
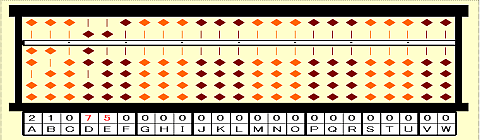
手順18:立方根は75と求まる。

最終状態: 答 75
珠の状態推移を表にすると次のようになる。(クリックで拡大)

同じ問題の三分九九法での解法と比べてみてほしい。
第18回も開立法(3根法)である。
関連記事:
ファインマン v.s. 算盤の達人: ファインマン先生に立方根計算の雪辱を果たそう
http://blog.goo.ne.jp/ktonegaw/e/89a0b907577f03ef6132cf9664bdcddb
目次:算盤による平方根、立方根の計算(開平、開立)
http://blog.goo.ne.jp/ktonegaw/e/bb0449f357398a2c24026f33af7f70ee
開平と開立(第40回):421,875の算盤による開立(三分九九法2)
http://blog.goo.ne.jp/ktonegaw/e/50897129d5551ee3e045b0afd0ab4d36
ブログ執筆のはげみになりますので、1つずつ応援クリックをお願いします。
























